|
23 |
規格第2版のPMHF式の疑問 (12) - パターン1 |
パターン1
再度、ISO 26262第2版解説書に示された導出過程に沿ってPMHF式を導出します。この導出過程によればパターン2に重大な誤りがあります。その原因はIFのフォールトの積分範囲なのですが、次稿で説明します。
図309.1の再掲になりますが図476.1に解説書のパターン1の導出過程を引用します。

時刻$t$がSM1のフォールト発生時刻、時刻$t'$が引き続くIFのフォールト発生時刻です。$t$と$t'$の制約を示します。 $$ \begin{eqnarray} \begin{cases} t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime} \\ t': \text{Time of fault of IF}, t\le t'\le T_\text{lifetime} \end{cases} \end{eqnarray}\tag{476.1} $$
図476.1ではパターン1のIFのフォールトの積分範囲、つまり$t'$の範囲は$t\le t'\le T_\text{lifetime}$となっています。従って、$t$が大となるに従って$t'$の範囲が狭くなり、IFのフォールト発生確率も小さくなります。つまり、$t$と$\Pr\{\text{IF fails at }t'\}$は逆相関の関係があります。
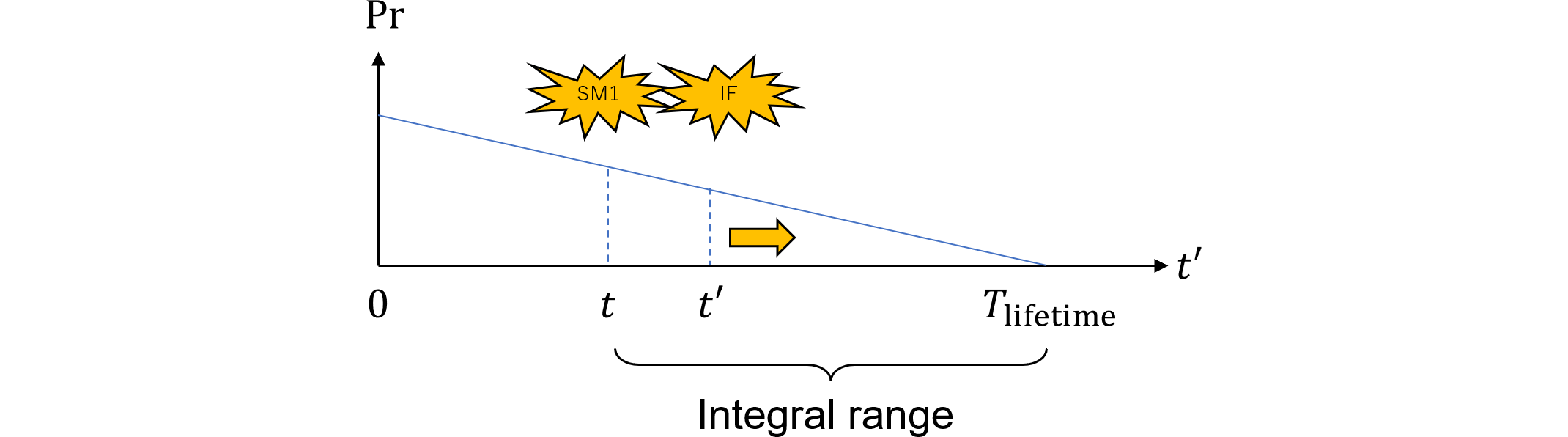
基本的には解説書に従った導出過程で計算しますが、誤りを修正します。まずIFのフォールトに関する積分である、「時刻$t$までup、かつ、$t'$でフォールトする確率」という以下の式(476.2)(図476.1から抜粋引用)は $$ \int_t^{T_\text{lifetime}}f_\text{IF,DPF}(t')dt'\cdot R_\text{IF}(t)\quad\quad\color{red}{(誤りであるため注意)} \tag{476.2} $$ (476.3)に示す2か所が誤りとその修正です。ただしこの誤りはたまたま結果に影響しません。 $$ \begin{eqnarray} \begin{cases} R_\text{IF}(t)&\Rightarrow&R_\text{IF}(t')\quad\quad\text{(up条件)}\\ f_\text{IF,DPF}(t')&\Rightarrow&\lambda_\text{IF,DPF}\quad\quad\text{(down条件)} \end{cases} \end{eqnarray}\tag{476.3} $$
(476.3)はIFに関するup条件及びdown条件ですが、この両者は同じIFに関する事象であるため独立ではありません。down条件に関しては(66.8)で示す条件付き確率を用いる必要があります。従って(476.2)を(476.4)のように、「時刻$t'$までup、かつ、$t'$でフォールトする条件付き確率」と修正します。するとIFのフォールトに関する確率(476.2)は、 $$ \begin{eqnarray} &&\Pr\{\text{IF is in }LAT2S\cap\text{IF fails in }[t, T_\text{lifetime})\}\\ &=&\Pr\{\text{IF up at }t\cap\text{IF prevented}\cap\text{IF fails in }[t, T_\text{lifetime})\}\\ &=&\Pr\{\text{IF prevented}\}\int_t^{T_\text{lifetime}}\Pr\{\text{IF down in }[t', t'+dt')\cap\text{IF up at }t'\}\\ &=&K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\Pr\{\text{IF down in }[t', t'+dt')\ |\ \text{IF up at }t'\}\cdot\Pr\{\text{IF up at }t'\}\\ &=&K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\lambda_\text{IF}R_\text{IF}(t')dt'=K_\text{IF, DPF}\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\\ &=&K_\text{IF, DPF}\left\lbrack F_\text{IF}(t')\right\rbrack_t^{T_\text{lifetime}}=K_\text{IF, DPF}\left[F_{\text{IF}}(T_\text{lifetime})-F_\text{IF}(t)\right]\\ &\approx&K_\text{IF, DPF}\lambda_\text{IF}\left(T_\text{lifetime}-t\right) \end{eqnarray} \tag{476.4} $$ と表せます。ここで途中の式
$$ K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\lambda_\text{IF}R_\text{IF}(t')dt'=\int_t^{T_\text{lifetime}}\lambda_\text{IF,DPF}R_\text{IF}(t')dt' \tag{476.5} $$ と(476.2)を比較すると、(476.3)で示した解説書の2点の誤りが確認できます。
(476.4)により$t$におけるIFの車両寿命までのフォールト確率を表せました。$t\le t'$の条件下ではSMとIFのフォールトの確率は独立として掛け合わせることができるので、パターン1のPMHFは、 $$ \require{cancel} \begin{eqnarray} M_\text{PMHF,P1}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\text{SM1 down in }[t, t+dt)\cap\text{SM1 undetected}\\ & &\cap\ \text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}\Pr\{\text{SM1 undetected}\}\int_0^{T_\text{service}}\Pr\{\text{SM1 down in }[t, t+dt)\ |\ \text{SM1 up at }t\}\\ & &\cdot\Pr\{\text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}(1-K_\text{SM1,DPF})\int_0^{T_\text{lifetime}}\lambda_\text{SM1}R_\text{SM1}(t)\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{lifetime}-t\right)\right\}dt\\ &=&\frac{1}{T_\text{lifetime}}(1-K_\text{SM1,DPF})K_\text{IF,DPF}\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\lambda_\text{IF}\left(T_\text{lifetime}-t\right)dt\\ &\approx&\frac{1}{\bcancel{T_\text{lifetime}}}(1-K_\text{SM1,DPF})K_\text{IF,DPF}\lambda_\text{IF}\lambda_\text{SM1}\left\lbrack T_\text{lifetime}\bcancel{t}-\frac{1}{2}t^\bcancel{2}\right\rbrack_0^{T_\text{lifetime}}\\ &=&\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM1,DPF})\lambda_\text{IF}\lambda_\text{SM1}T_\text{lifetime}\\ &=&\frac{1}{2}\lambda_\text{SM1,DPF,lat}\lambda_\text{IF,DPF}T_\text{lifetime} \end{eqnarray} \tag{476.6} $$ となります。なお、式変形中に弊社積分公式(471.3)を使用しています。
結果の(476.6)は次の図476.3に引用する規格第2版式のパターン1と正確に一致します。導出のベースがIFUモデルとなっているのが理由です。

さらに(476.6)は、次の図476.4に引用する規格初版第1式のパターン1に相当する部分(黄色部分)とも(IF⇒mと読み替えることにより)正確に一致します。導出のベースがIFUモデルとなっているのが理由です。
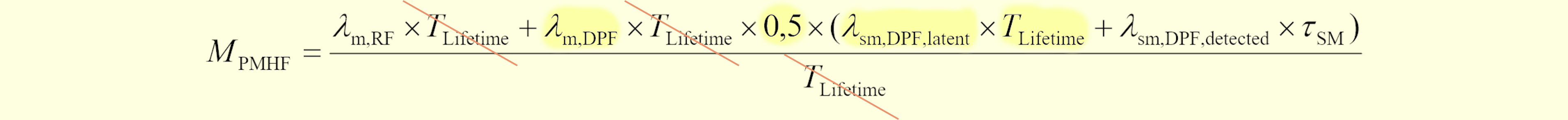
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。
