|
16 |
レイテントフォールトの問題 (3) |
第3問です。次の事象はレイテントフォールトになるかという問題で、その事象は、

というものです。
ちなみに、パナソニックのサイトによれば、
EMC(電磁両立性)とは、電気製品から放出する電気的ノイズを抑え(エミッション:EMI)、かつ周囲からの電気的ノイズによって電気製品がトラブルを起こさない(イミュニティ:EMS)ための2つの性能
とのことです。また、ノイズ対策.comによれば、
EMC(Electro-Magnetic Compatibility:電磁両立性)は、妨害電波を規制するEMI(Electro Magnetic Interference)と外来ノイズの耐性を示すEMS(Electro Magnetic Susceptibility) の2面があります。
とのことです。
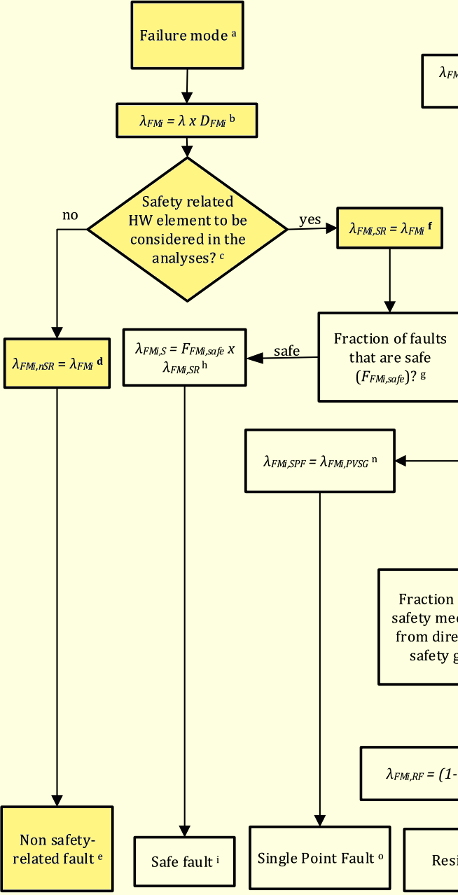
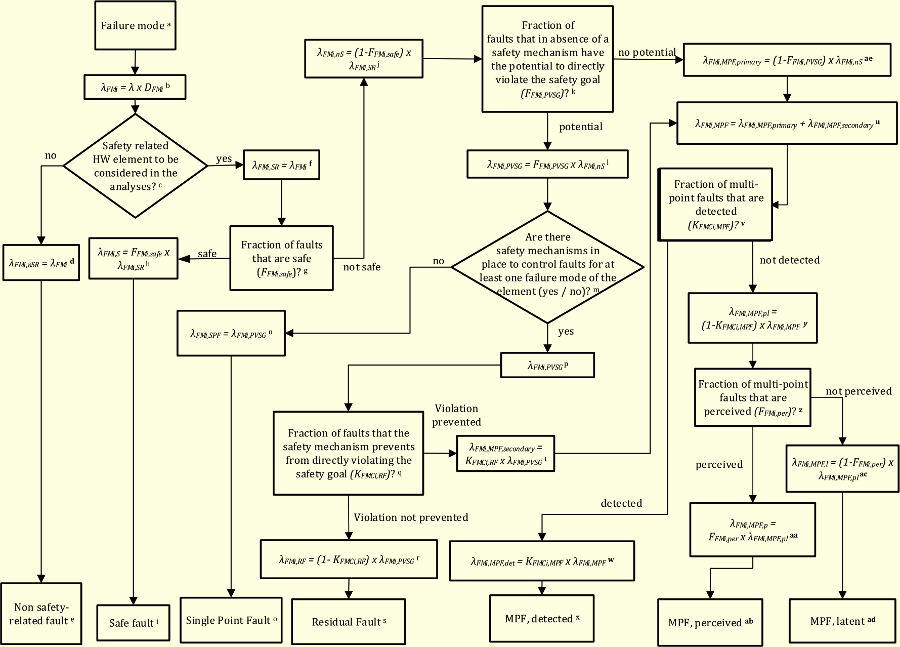
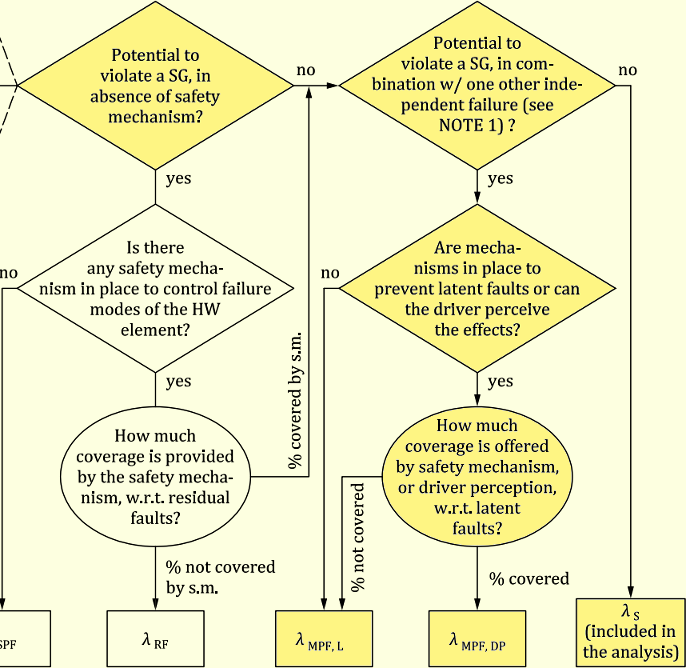
さて、前問と同様SRを補って考えます。安全機構(SM)であるEMC保護キャパシタは、EMCにより意図機能(IF)が動作失陥しないためのSMと想定します。例えば、外来ノイズが入るとマイコンが誤動作し、本来のSRを侵害する等が想定されます。SRとしては例えば、「意図せずにマイコンが誤動作しないこと」を想定します。
キャパシタのオープンフォールトにより、IFの保護がなくなります。従って、EMC保護キャパシタは、EMCによりIFがVSGとなるのを防止する1st SMとなります。ただし、注意が必要なのは、通常のようにIFのフォールトによりVSGとなるのではなく、IFにEMCが加わってVSGとなることです。そのため、普通のDPFとは異なりますが、これは後で説明します。
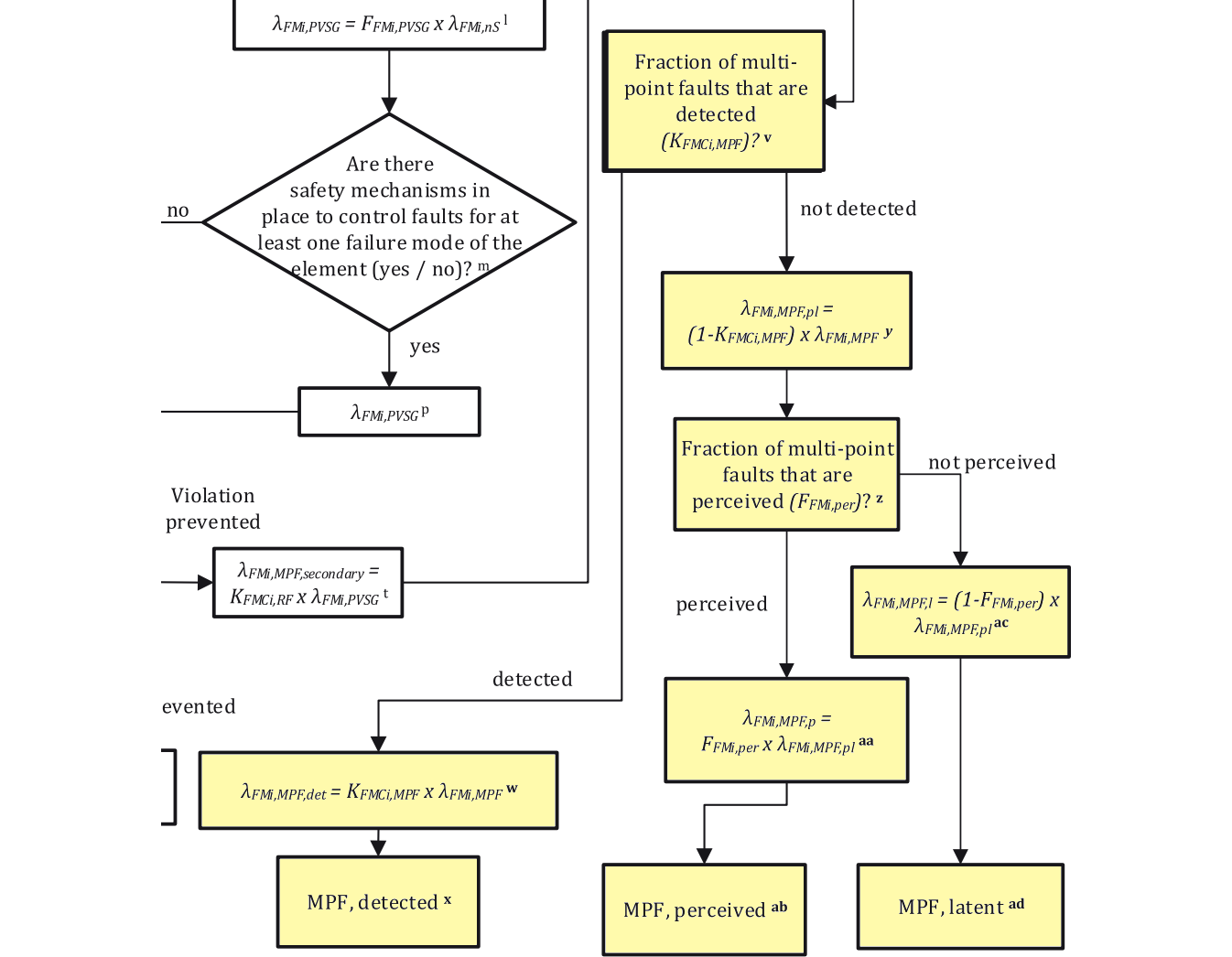
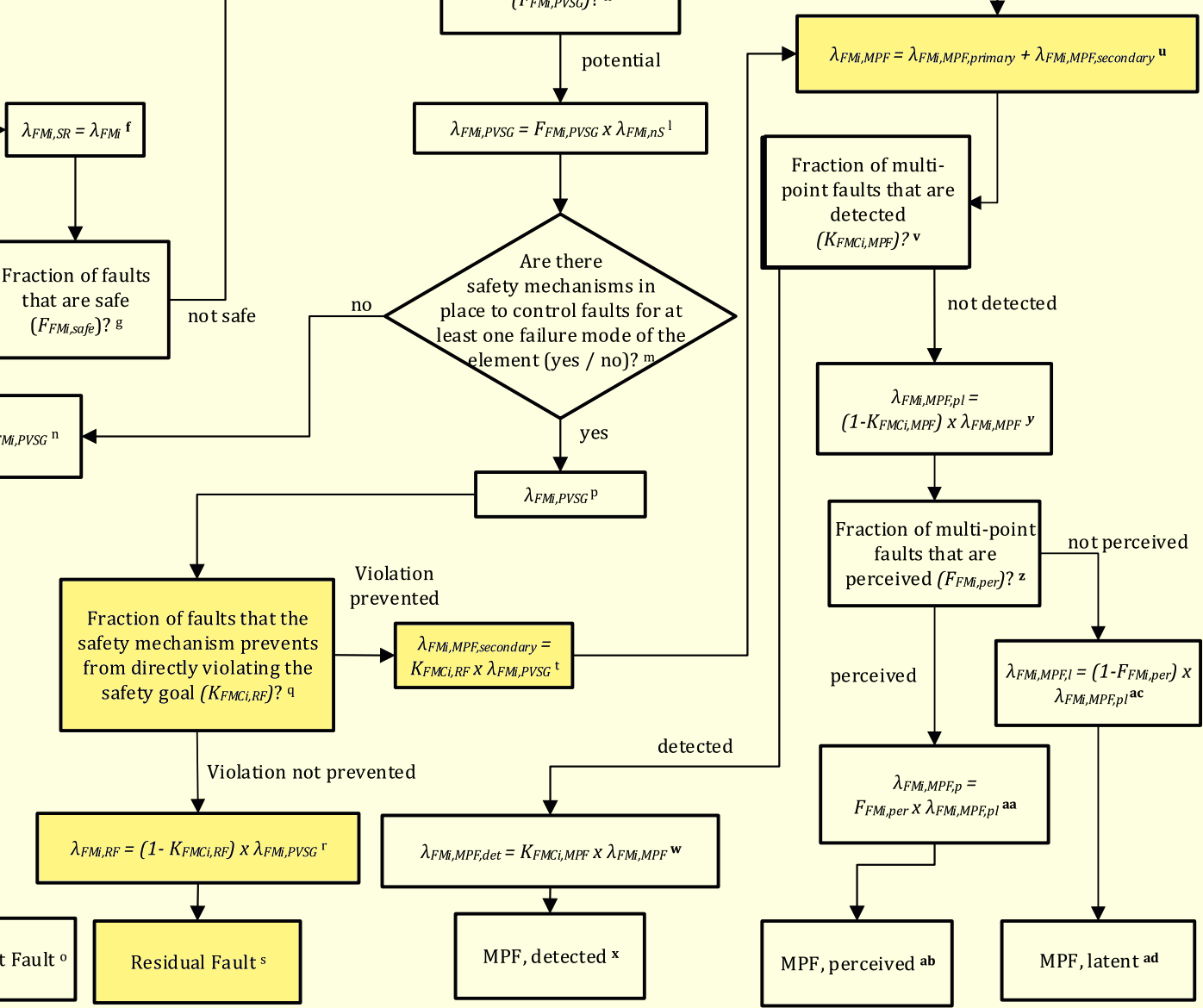
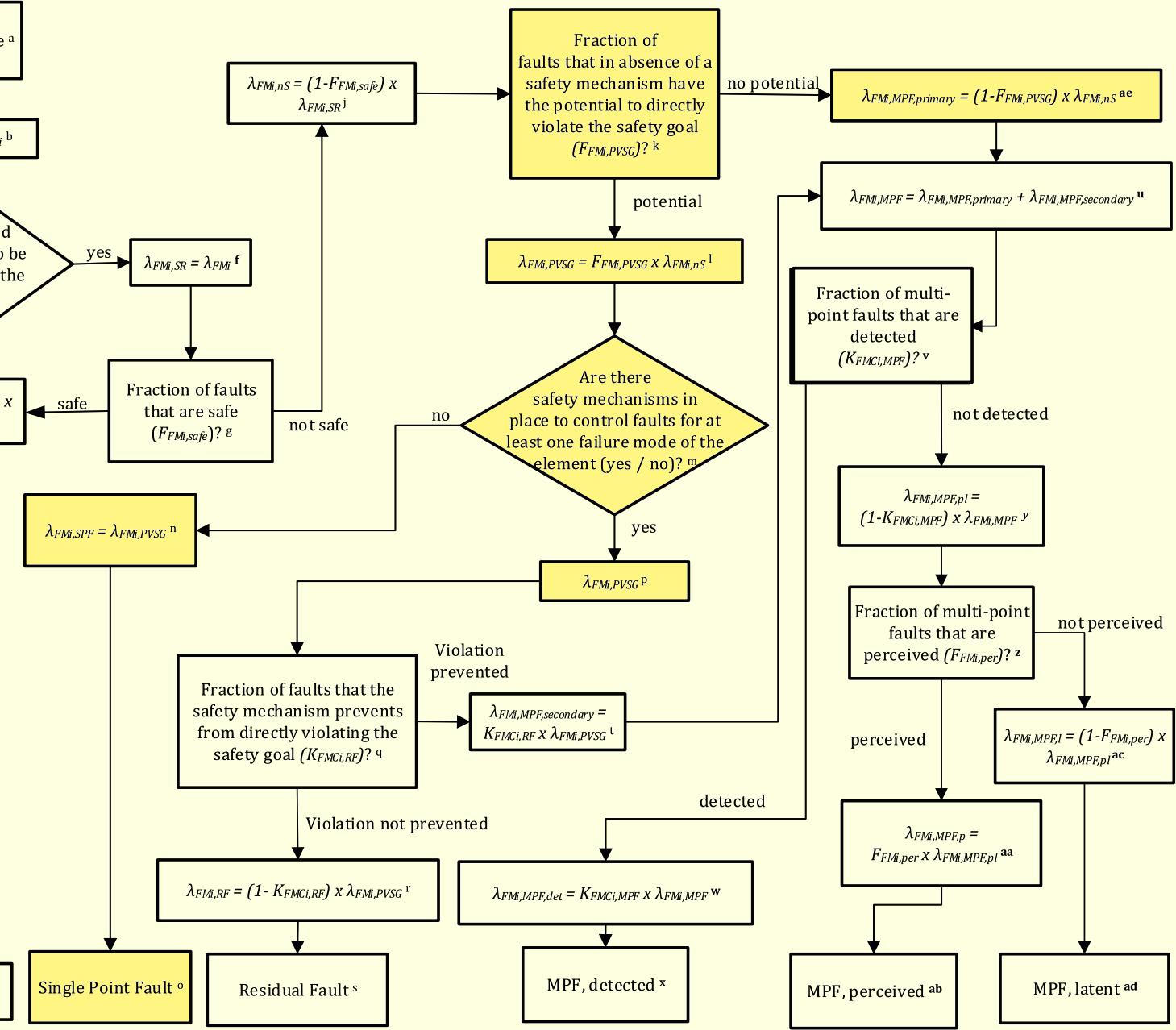
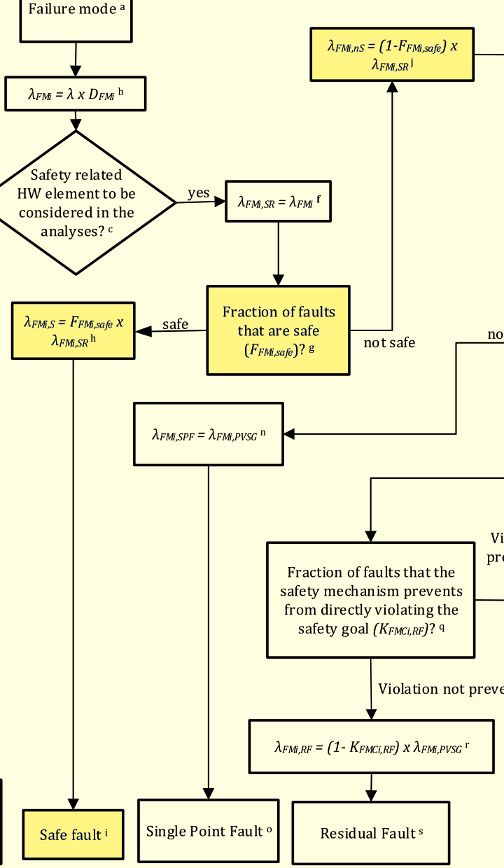
次に考慮することは、EMC保護キャパシタのオープンフォールトが、2nd SMにより検出され通知されるかどうかです。EMC保護キャパシタは通常2nd SMにより保護されていないので、レイテントフォールトになります。このことは規格Part5 Annex EのFMEDAシートでレイテントフォールトと分類されていることからも確認されます。
一方で、規格Part5 Annex E Note 3に例外的な記述があり、
If for example the ESD event is likely to occur during the vehicle lifetime and its effects can lead to the violation of the safety goal in the absence of the given protection, then the failure mode leading the loss of the protection is classified as a single-point fault.
例えば、車両の寿命中にESDイベントが発生する可能性が高く、その影響が与えられた保護がない場合に安全目標の違反につながる可能性がある場合、保護を失う原因となる故障モードは単一点故障に分類されます。
とあるため、EMCが車両寿命中に発生する可能性が高い場合は、IFがすでに動作欠陥し、かつEMC保護キャパシタでVSG抑止していると考えるため、EMC保護キャパシタのオープンフォールトはSPFとなります。
ここではEMC(EMI/EMS)やESDを電磁的な外来ノイズとして、フォールトと同様な事象と扱いました。これらはフォールトではないものの、上記のように、通常はEMC保護キャパシタのオープンフォールトはLFとして良く、EMC/ESDの頻度が高ければSPFと扱うことになります。そのため、焦点はEMCの頻度になります。
FMEDAにおいてEMCをフォールト扱いしていることからわかるように、頻度の判定はフォールト基準で考えます。頻度としては10~100FIT程度、確率は、車両寿命を10万時間とすれば0.1~1%でしょうか。それを超える場合は高頻度として扱うことになります。
最後に、EMC保護キャパシタのオープンフォールトがSF(Safe Fault)とできるかどうかですが、そもそもEMCが印加されることが無いのなら、EMC保護キャパシタも不要です。その対偶をとり、EMC保護キャパシタが存在する以上、稀にでもEMCが印加されることはあると考え、EMC保護キャパシタのオープンフォールトは、 $\img[-1.35em]{/images/withinseminar.png}$ とするのが妥当と考えます。