On October 22, 2022, a paper by Atsushi Sakurai, CEO of FS Micro Corporation (Head Office: Nagoya, Japan), a leading provider of functional safety (Note 1) consulting services, was formally accepted by RAMS (Note 2) 2023, an international conference on reliability organized by IEEE (Note 3). This is the fourth consecutive year that the author's paper has been accepted to RAMS. The author also received the Best Paper Award at the 14th ISPCE 2017 (Note 4), an international conference hosted by IEEE in 2017.
RAMS 2023 is scheduled for January 23-26, 2023, at the Florida Hotel and Conference Center in Orlando, Florida, USA.

In 2018, the second edition of ISO 26262 (Note 5), the international standard for functional safety in automotive electronics, was published, and the PMHF (Note 6) equation was also revised. At RAMS 2020, the author clarified the mathematical background of the PMHF formula and proposed a new PMHF formula with which optimal values can be calculated.
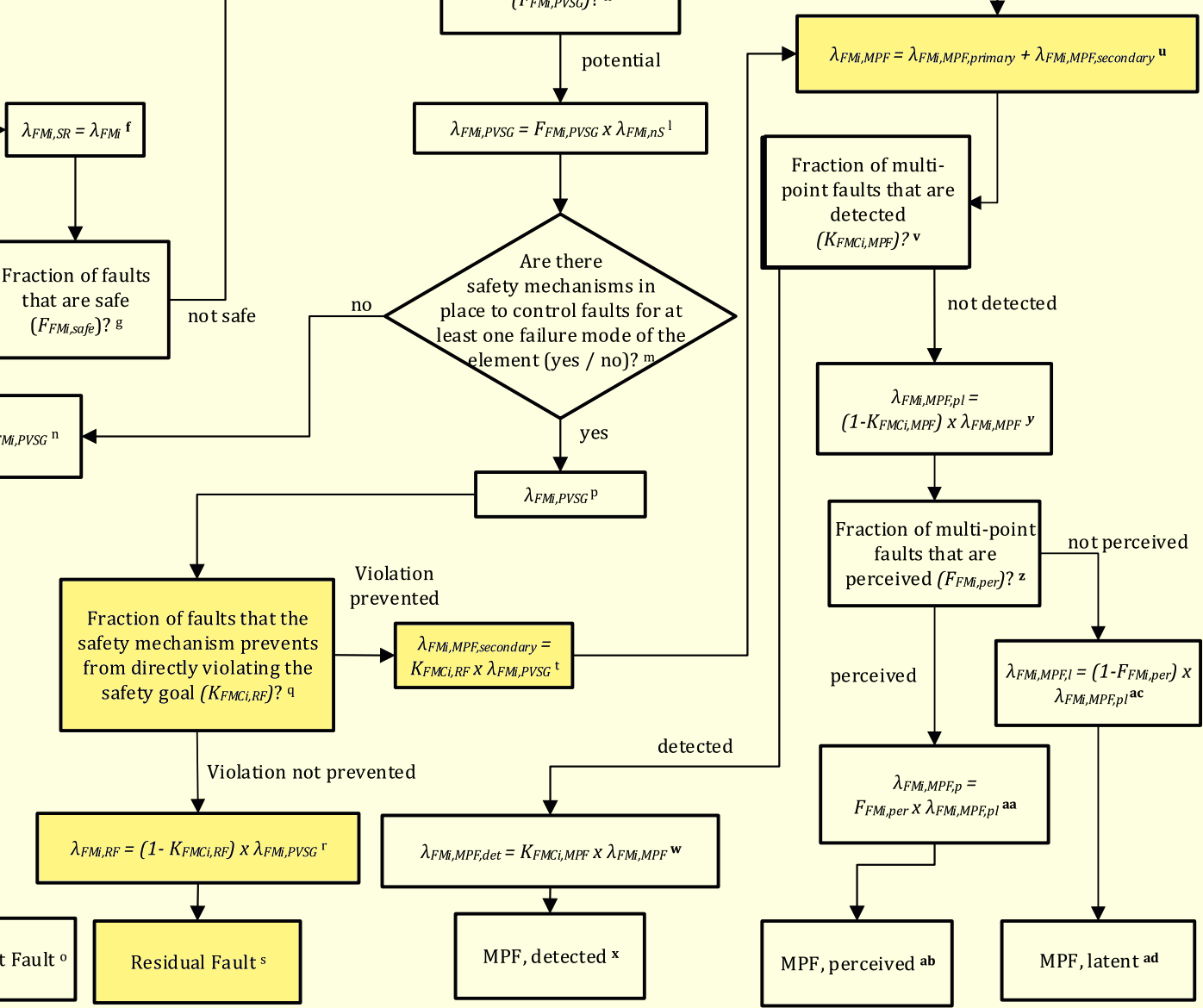
This paper re-proves the author's PMHF formula by using the newly proposed stochastic constituents. Specifically, the PMHF formula in ISO 26262 Edition 1 is decomposed into stochastic constituents by considering the combined elements of the intended function and the safety mechanism, and the PMHF formula is proved to be the PMHF formula in the case where the intended function and the safety mechanism are repairable. This makes it possible to prevent overestimation of the PMHF, which has been seen in the past. As a result, it is expected to reduce design man-hours and time-to-market for fault-tolerant systems (Note 7), as represented by self-driving systems.
Company name: FS Micro Corporation
Representative: Atsushi Sakurai
Date of establishment August 21, 2013
Capital: 32 million yen
Business description Consulting and seminars on functional safety of ISO 26262 automotive electronic devices
Address of Head Office 460-0011 4-1-57 Osu, Naka-ku, Nagoya, Aichi, Japan
Phone: +81-52-263-3099
E-mail address info@fs-micro.com
URL http://fs-micro.com/
Notes
Note 1: Functional safety is the concept of enhancing safety at the system level by taking various safety measures.
Note 2: IEEE stands for the Institute of Electrical and Electronics Engineers. It is the world's largest conference on electrical and electronic engineering technology in terms of number of participants and participating countries. http://ieee.org/
Note 3: RAMS stands for The 69th Annual Reliability & Maintainability Symposium, an international conference on reliability engineering organized annually by the IEEE Reliability Society. http://rams.org/
Note 4: ISPCE stands for IEEE Symposium on Product Compliance Engineering, an international conference on product safety organized annually by the IEEE Product Safety Society. http://2017.psessymposium.org/
Note 5: ISO 26262 is a functional safety standard for in-vehicle electrical and electronic systems, an international standard that aims to reduce the possibility of dangerous events to an acceptable level occurring during vehicle operation due to malfunctions of in-vehicle electrical and electronic systems.
Note 6: PMHF stands for Probabilistic Metric for Random Hardware Failures. It is one of the design target values for hardware in ISO 26262, which is a time average of the probability of system failure during the vehicle lifetime.
Note 7: Fault-tolerant systems are safety-enhancing systems that can substitute the original function without immediately losing the function in the event of a failure.
 前のブログ
次のブログ
前のブログ
次のブログ