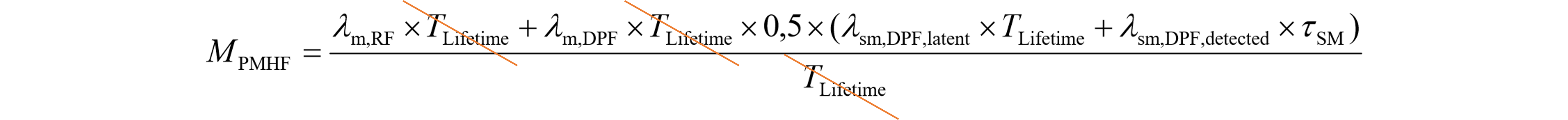LAT2⇒DPF1の平均PUDの計算
IFRモデルのLAT2からDPF1への平均PUDの計算を行いますが、MPF detectedの寄与分を改訂します。前稿#107での計算を基本として、MPF detectedが即修理となるため、IFのVSG preventable部分の稼働確率が上がります。従って、LAT2のIF preventable部分の稼働確率も同じだけ上がります。
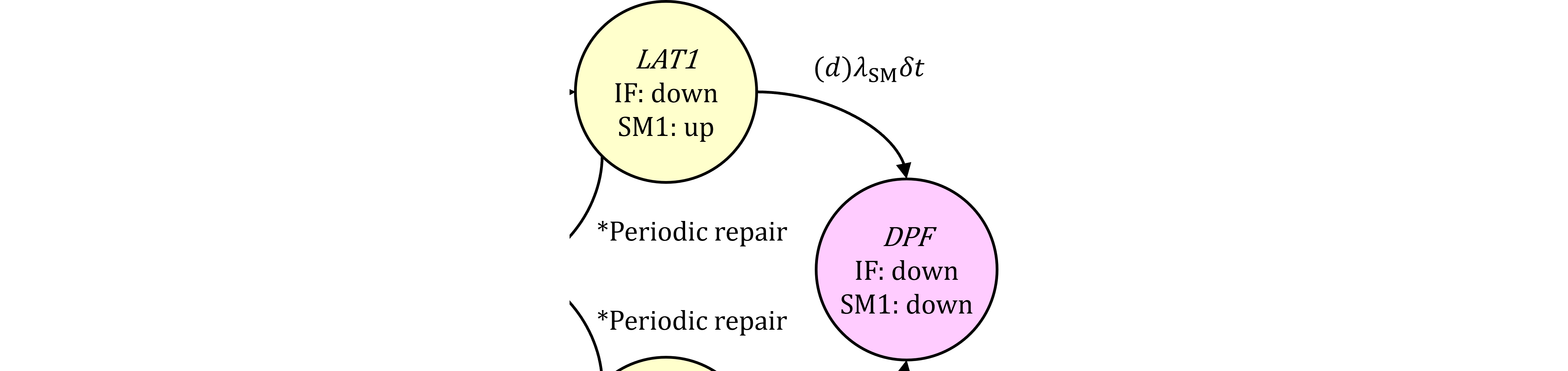
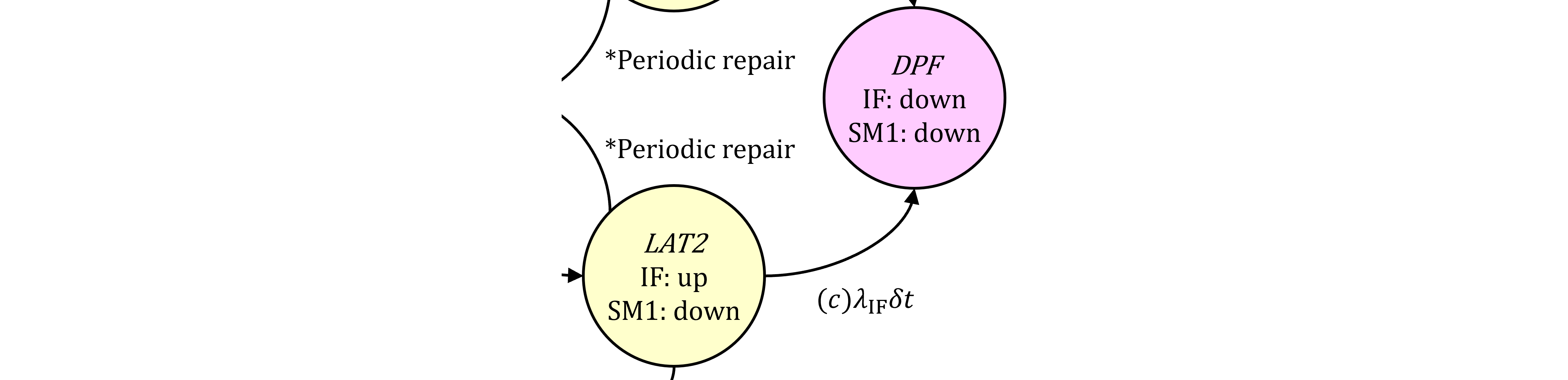
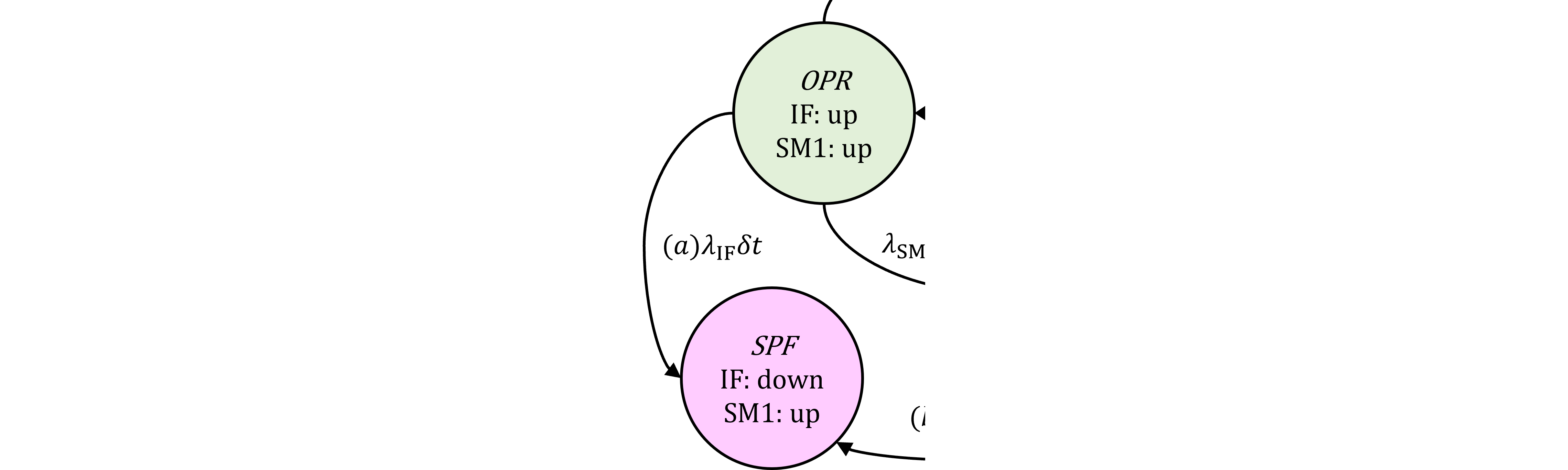
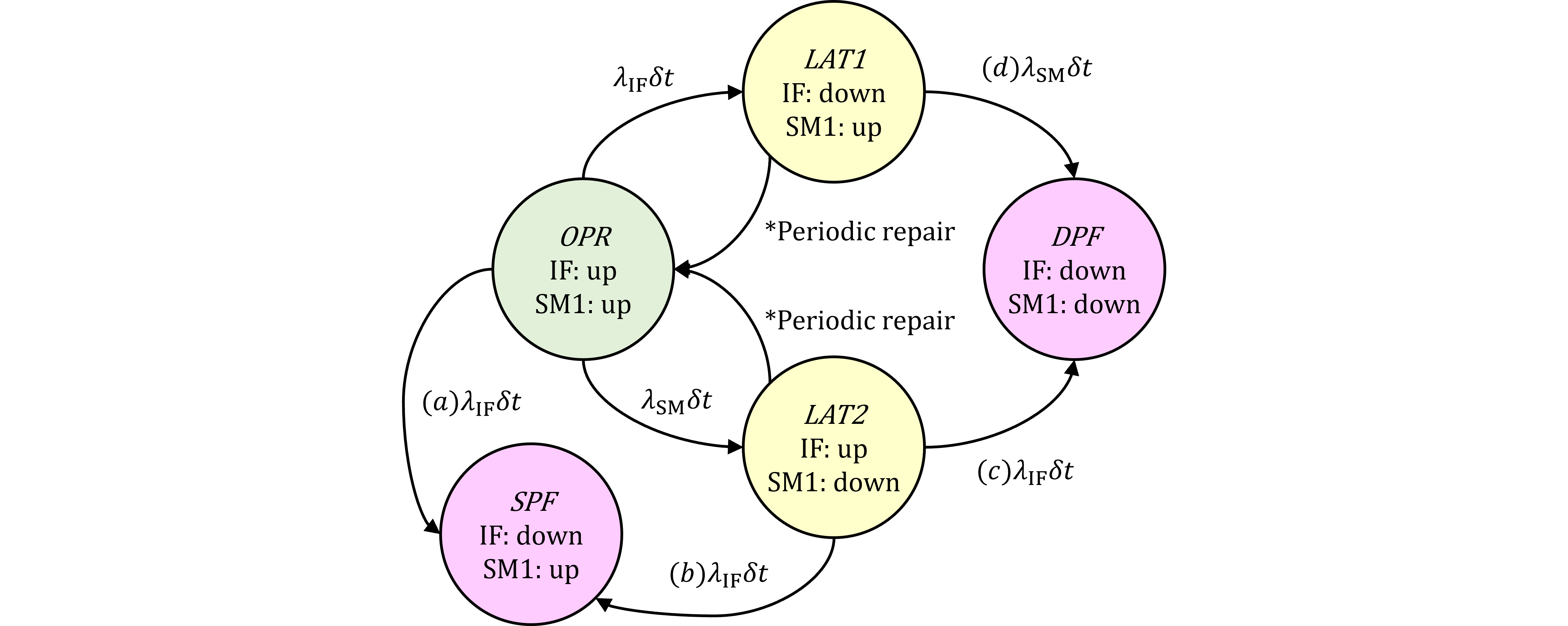
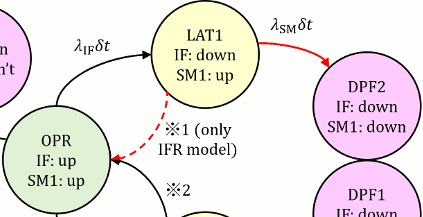
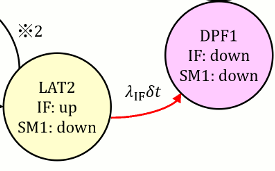図362.1 CTMCにおいてLAT2⇒DPF1の遷移
前稿#107の式(107.1)はそのままです。LAT2からDPF1への平均PUDは、
$$
\begin{eqnarray}
\overline{q_{\mathrm{DPF1,IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF1\ at\ }T_\text{lifetime}\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\ \mathrm{IF\ down\ in\ }(t, t+dt]\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\
& &\cdot\Pr\{\mathrm{LAT2}\mathrm{\ at\ }t\}
\end{eqnarray}
\tag{362.1}
$$
LAT2は、基本的にはIFの稼働状態でかつSM1の不稼働状態ですが、MPF detectedの定義である、
- IFの不稼働
- SM1による検出
- VSGとはならない
の3条件を満たす部分も稼働とみなすため、赤字の条件を追加します。さらに(355.1)を用いて書き換えると、
$$
\begin{eqnarray}
\Pr\{\mathrm{LAT2\ at\ }t\}&=&\Pr\{(\mathrm{IF^R\ up\ at\ }t\\
& &\color{red}{\cup\ (\mathrm{IF^R\ down\ at\ }t\ \cap\ \mathrm{IF^R\ detectable}\ \cap\ \mathrm{IF^R\ preventable})})\\
& &\cap\ \mathrm{SM\ down\ at\ }t\}\\
&=&(\Pr\{\mathrm{IF^R\ up\ at\ }t\}+\Pr\{\mathrm{IF^R\ down\ at\ }t\}\\
& &\color{red}{\cdot\Pr\{\mathrm{IF^R detectable}\ |\ \mathrm{IF^R preventable}\}}\cdot\Pr\{\mathrm{IF^R preventable}\})\\
& &\cdot\Pr\{\mathrm{SM\ down\ at\ }t\}\\
&=&\left[(1-K_{\text{IF,RF}})R_\text{IF}(t)+K_{\text{IF,RF}}A_\text{IF}(t)+\color{red}{K_\text{det}}K_\text{IF,RF}Q_\text{IF}(t)\right]Q_{\mathrm{SM}}(t)
\end{eqnarray}\tag{362.2}
$$
となります。この場合、$\Pr\{\mathrm{IF^R\ up\ at\ }t\}$は、$\text{IF preventable}$と$\overline{\text{IF preventable}}$のORであり、DPFの意味では前者のみなのですが、形式上SMがdownしている状態であるため、SPFもDPF扱いとなるので、両方の場合を含めています。ちなみに、
$$
\begin{eqnarray}
\Pr\{\mathrm{IF^R\ up\ at\ }t\}&=&\Pr\{(\mathrm{IF^U\ up\ at\ }t\ \cap\ \overline{\text{IF preventable}})\\
& &\cup\ (\mathrm{IF^R\ up\ at\ }t\ \cap\ \text{IF preventable})\}\\
&=&(1-K_{\text{IF,RF}})R_\text{IF}(t)+K_{\text{IF,RF}}A_\text{IF}(t)
\end{eqnarray}\tag{362.3}
$$
を(362.2)に用いています。
一方、(107.7)と同様に
$$
\require{cancel}
\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\
=\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\cap\ \bcancel{\mathrm{SM\ down\ at\ }t}\}\\
=\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}=\lambda_{\mathrm{IF}}dt\tag{362.4}
$$
となります。よって、LAT2からDPF1への平均PUDは、
$$
\begin{eqnarray}
\overline{q_{\mathrm{DPF1,IFR}}}&=&\frac{1-K_\mathrm{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt+\frac{K_\mathrm{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)A_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt\\
& &+\frac{\color{red}{K_\text{IF,det}}K_\mathrm{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)(1-A_{\mathrm{IF}}(t))\lambda_{\mathrm{IF}dt}\\
&=&\frac{1-K_\mathrm{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\mathrm{SM}(t)f_{\mathrm{IF}}(t)dt\\
& &+\frac{K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\mathrm{SM}(t)q_\mathrm{IF}(t)dt\\
& &+\frac{\color{red}{K_\text{det}}K_\mathrm{IF,RF}\lambda_\mathrm{IF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)dt\\
&=&\frac{1-K_\mathrm{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_\mathrm{SM,MPF})F_{\mathrm{SM}}(t)+K_\mathrm{SM,MPF}F_{\mathrm{SM}}(u)]f_{\mathrm{IF}}(t)dt\\
& &+\frac{K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_\mathrm{SM,MPF})F_{\mathrm{SM}}(t)+K_\mathrm{SM,MPF}F_{\mathrm{SM}}(u)]\\
& &\cdot\left[(1-K_\mathrm{IF,MPF})f_{\mathrm{IF}}(t)+K_\mathrm{IF,MPF}f_{\mathrm{IF}}(u)\right]dt\\
& &+\frac{K_\mathrm{IF,RF}\color{red}{K_\text{det}}\lambda_\text{IF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_\mathrm{SM,MPF})F_{\mathrm{SM}}(t)+K_\mathrm{SM,MPF}F_{\mathrm{SM}}(u)]dt\\
\end{eqnarray}\tag{362.5}
$$
これに(360.5)及び(360.8)を用いて、
$$
\begin{eqnarray}
(362.5)&\approx&\frac{1-K_\mathrm{IF,RF}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau]\\
& &+\frac{K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-
K_\mathrm{MPF})T_\text{lifetime}+K_\mathrm{MPF}\tau]\\
& &+\frac{K_\mathrm{IF,RF}\color{red}{K_\text{det}}}{2}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau]\\
&=&(1-K_\mathrm{IF,RF}+K_\text{IF,RF}\color{red}{K_\text{det}})\alpha+K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta,
\end{eqnarray}\tag{362.6}
$$
$$
ただし、\begin{cases}
\begin{eqnarray}
u&:=&t\bmod\tau\\
\alpha&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau]\\
\beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{MPF})T_\text{lifetime}+K_\mathrm{MPF}\tau]\\
K_\mathrm{MPF}&:=&K_\mathrm{IF,MPF}+K_\mathrm{SM,MPF}-K_\mathrm{IF,MPF}K_\mathrm{SM,MPF}\\
&=&1-(1-K_\mathrm{IF,MPF})(1-K_\mathrm{SM,MPF})
\end{eqnarray}
\end{cases}
$$
RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。
前のブログ
次のブログ
