|
6 |
FTAのtree logic (4) |
この65項の積項から成る論理式が簡単化できるか、ChatGPTに聞いてみます。
以下は与えられた論理式(縦方向がOR、行中のコンマでAND)の因数分解結果です。
(略)
集合Aを $$ A := \{BE001\_01, BE001\_02, BE001\_03, BE001\_05, BE001\_09, BE014\_01, BE027, BE028\} $$ とし、集合Bを $$ B := \{BE002\_01, BE002\_02, BE002\_03, BE002\_09, BE002\_15, BE015\_01, BE030, BE031\} $$ とすると、上記64行はすべて$(a \land b)$で$a \in A, b \in B$の組み合わせによる全ての直積を網羅しています(8×8=64)。
従って、64行分は以下のように因数分解できます。
$$ \bigvee_{a \in A}\bigvee_{b \in B}(a \land b) \\ = (BE001\_01 \lor BE001\_02 \lor BE001\_03 \lor BE001\_05 \lor BE001\_09 \lor BE014\_01 \lor BE027 \lor BE028) \\ \land (BE002\_01 \lor BE002\_02 \lor BE002\_03 \lor BE002\_09 \lor BE002\_15 \lor BE015\_01 \lor BE030 \lor BE031) $$
さらに、元の式にはこれら64個のAND項に加えて1行目に単独のリテラル$BE025$で存在するので、全式は次のようになります。
$$ BE025\\ \bigl((BE001\_01 \lor BE001\_02 \lor BE001\_03 \lor BE001\_05 \lor BE001\_09 \lor BE014\_01 \lor BE027 \lor BE028)\\ \land (BE002\_01 \lor BE002\_02 \lor BE002\_03 \lor BE002\_09 \lor BE002\_15 \lor BE015\_01 \lor BE030 \lor BE031)\bigr) $$
これが要求された因数分解後の論理式です。
この論理式をFT図にすれば過去記事のとおり、次の図のようになります。
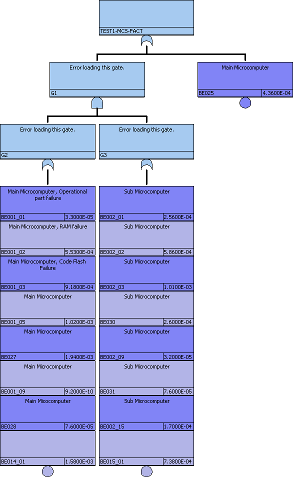
BE001はメインマイコンであり、BE001_*はメインマイコン各部のフォールトです。さらに、BE002はサブマイコンであり、BE002_*はサブマイコン各部のフォールトです。
従って、このFTはメインマイコン各部とサブマイコン各部のフォールトがいずれか一個の計2個起きるか、またはPCB上の電源ICがフォールト(BE025)するかのいずれかであり、マイコンとしては冗長構成をとる、安全性の高い回路となっていることがわかります。
