最急降下法は問題があります。例えば、 $$f(x_1,x_2,x_3)=x_1^2+\frac{x_2^2}{20}+x_3^2$$ のような関数があったときの収束曲線を見てみると次のような図になります。

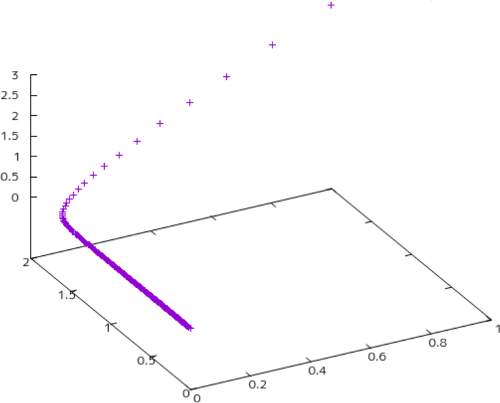
こうなるのは、出発点から見て、関数の最小値(あるいは極小値)のある方向が、出発点の最も傾斜が急な方向と、必ずしも一致しないためです。

前述のように、一段のニューロンだとフィッティングに制限がありますが、さらに隠れ層のレイヤを加え、活性化関数の非線形性を導入することで、より自由な関数へのフィッティングが可能となります。

フィッティングをどのように実施するかですが、バックプロパゲーションを行います。バックプロパゲーションは、結果値が正解値とどれだけ乖離しているかを損失関数により評価し、それを各レイヤの重みベクトル$\boldsymbol{w}$に変換して、後段から前段に向かって伝えるものです。

このときに勾配テンソルが偏微分のチェインルールにより、後段から前段に向かって次々に簡単に求められるところがミソです。

前のブログ 次のブログ