最急降下法
最適化の手法として最急降下法がしばしば用いられます。本来は、n次元ベクトル空間でのコスト関数の最小解が知りたい場所ですが、最小解を解くことは困難なので、極小解を求めます。出発点のまわりの谷底を見つけるわけであり、谷に下っていく方法のひとつとして、最も傾斜のきつい方向に降りることを最急降下法と呼びます。
最も勾配の大きい方向ベクトルを求めるため、以下の式のようにベクトル要素の偏微分をとるハミルトニアン演算子を使用します。
$$\nabla f=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\right)$$
このハミルトニアン演算子を用いると、最急降下法による変位ベクトルは以下のように簡略に記述できます。
$$\varDelta\boldsymbol{x}=-\eta\nabla f$$
ここで$\eta$は正の小さい数、例えば0.1とします。これは学習率と呼ばれます。
これを具体的に見てみます。例えば、
$$f(x_1,x_2,x_3)=x_1^2+x_2^2+x_3^2$$
という関数があるとき、その偏微分は
$$\frac{\partial f}{\partial x_1}=2x_1, \frac{\partial f}{\partial x_2}=2x_2, \frac{\partial f}{\partial x_3}=2x_3$$
となります。点$(1.0, 2.0, 3.0)$から開始して最急降下法による漸化式をExcelで実行させてみました。
| 繰り返し回数 |
$x_1$ |
$x_2$ |
$x_3$ |
$\frac{\partial f}{\partial x_1}$ |
$\frac{\partial f}{\partial x_2}$ |
$\frac{\partial f}{\partial x_3}$ |
$\Delta x_1$ |
$\Delta x_2$ |
$\Delta x_3$ |
| 0 |
1.000 |
2.000 |
3.000 |
2.000 |
4.000 |
6.000 |
-0.200 |
-0.400 |
-0.600 |
| 1 |
0.800 |
1.600 |
2.400 |
1.600 |
3.200 |
4.800 |
-0.160 |
-0.320 |
-0.480 |
| 2 |
0.640 |
1.280 |
1.920 |
1.280 |
2.560 |
3.840 |
-0.128 |
-0.256 |
-0.384 |
| : |
| 41 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.001 |
-0.000 |
-0.000 |
-0.000 |
| 42 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.001 |
-0.000 |
-0.000 |
-0.000 |
| 43 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
-0.000 |
-0.000 |
-0.000 |
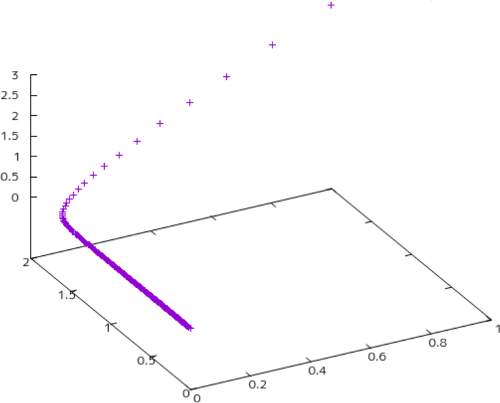
のように、43回目で偏微分が全て小数点3桁までゼロとなり、局所最小値$(0.0, 0.0, 0.0)$が求められました。図91.1にこの座標$(x_1, x_2, x_3)$の推移を示します。偏微分で求めた勾配を逆に下っていく様子が現れています。
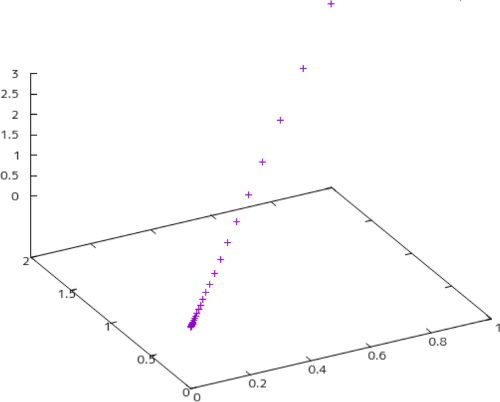図91.1 座標位置の推移
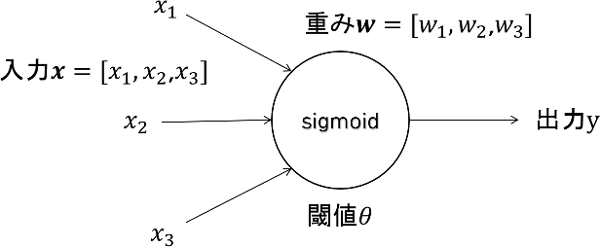
前稿のシグモイドニューロンを多層化することにより、任意の分類が行えるようになります。
前のブログ
次のブログ
