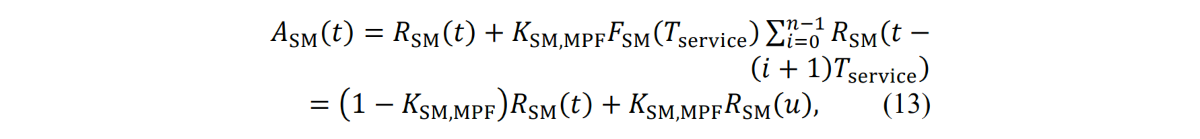次は(15)の導出です。
論文"Generic Equations for a Probabilistic Metric for Random Hardware Failures According to ISO 26262"において、以下の2か所の式変形過程が分からないが、どうして次の式(13), (15)が導出されるのか?
(13) 省略、前ページで解説

これは既に過去ブログでも記載済みなのでその箇所を返信しました。
Equation (103.6) in the following blog post is what you are looking for.
次のブログ記事の式(103.6)があなたが探しているものです。
https://fs-micro.com/post/show/id/103.html
Here's the trick: we transform it using $F(t)$ instead of $R(t)$. Because our integral
formula
ここにトリックがあります。$R(t)$の代わりに$F(t)$を用います。なぜなら、我々の積分公式
https://fs-micro.com/post/show/id/60
can be used.
が使えるからです。
返信の際に$F(t)$に言及したのは、読者の方がご自分で変形し、$R(t)$の形式を導出した後行き詰っていたのでヒントを示しています。以下に記事の(103.6)を再掲します。
よって、(103.1)に(103.1.5)、(103.1.3)、$\Pr\{\overline{\text{VSG of IF preventable}}\}=1-K_\text{IF,RF}$(100.3)を用いた上で、故障率(66.6)及びPUA(59.8)を適用すれば、平均PUDは、
$$
\begin{eqnarray}
\overline{q_\text{SPF,IFU}}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\text{IF,RF})R_\text{IF}(t)A_\text{SM}(t)\lambda_\text{IF}dt\\
&=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[1-Q_\text{SM}(t)\right]f_\text{IF}(t)dt\\
&=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_\text{IF}(t)dt-\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\text{SM}(t)f_\text{IF}(t)dt\\
&=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}F_\text{IF}(T_\text{lifetime})\\
& &-\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_\text{SM,MPF})F_\text{SM}(t)+K_\text{SM,MPF}F_\text{SM}(u)\right]f_\text{IF}(t)dt,\\
& &\text{ただし、}u:=t\bmod\tau
\tag{103.1.6}
\end{eqnarray}
$$
よって、$F_\text{IF}(t)=1-e^{-\lambda_\text{IF}t}\approx\lambda_\text{IF}t$と近似する0におけるTaylor展開(すなわちMaclaurin展開)及び弊社積分公式により、
$$
\overline{q_\text{SPF,IFU}}\approx(1-K_\text{IF,RF})\lambda_\text{IF}-\frac{1-K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}\tau\right]\\
\tag{103.1.7}
$$
1st editionでは定期修理期間を$\tau$で表していましたが、2nd editionでは表記が$T_\text{service}$に変わりました。従って、
$$
\overline{q_\text{SPF,IFU}}\approx(1-K_\text{IF,RF})\lambda_\text{IF}-\frac{1}{2}(1-K_\text{IF,RF})\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}T_\text{service}\right]
$$
となり、(15)が成立します。
 前のブログ
次のブログ
前のブログ
次のブログ