|
31 |
定量FTAによるPMHF計算法 (3) |
前ページ右下のORゲートから左下への事象です。これはRFの項を表しており、ALUのフォールトカバレージ残余である$1-DC$が接続されています。
ここで確率に着目すれば、 $$ Q=1-DC_\text{1}=0.8=8.00\times10^{-1}より\\ DC_\text{1}=20\% \tag{587.1} $$ と逆算されます。$DC_\text{1}$のような無次元の定数にはミッションタイムは自動掛算されません。
次に同じくORゲートから右下への事象です。これはDPF確率を示すANDゲートです。
このANDゲートの左下への分岐はLFのサブツリーとなっています。
右下への事象はIFのDPFフォールトを表す事象で、具体的にはSM1でVSG抑止された部分である$DC$を示しています。 $$ Q=DC_\text{1}=0.2=2.00\times10^{-1}より、\\ DC_\text{1}=20\% \tag{587.2} $$ となっています。
|
30 |
定量FTAによるPMHF計算法 (2) |
図585.1が小さいので拡大して見ていきます。まず部分FTのトップのANDゲートです。車両寿命間におけるALUの永久故障確率を表しています。
ANDゲートの左下の事象はALUの永久故障率です。ALUの2つの数字、故障率と確率に着目すれば、本文に$T_\text{lifetime}=5,000[H]$とあることを用いて、 $$ \lambda_\text{IF}=3.48\times10^{-11} および\\ Q=\lambda_\text{IF}T_\text{lifetime}=3.48\times10^{-11}\cdot5.0\times10^{3}=1.74\times10^{-7}\tag{586.1} $$ となります。
事象には故障率$\lambda_\text{IF}$を入力します。ここで故障率は$[H^{-1}]$の次元を持つため、FTAツールがデフォールトのミッションタイム(運用時間)である車両寿命$T_\text{lifetime}$を自動的に掛け、確率$Q$に直して計算します。
注目すべき記号としてLがあります。これはプライオリティを示すもので、Lで示される側のフォールトが後で生起する場合に限定されます。従って本FTはフォールト順序がSM1⇒IFの順であり、冗長性は持たないという前提です。すなわちDPF項には$\frac{1}{2}$が必要です。
トップのANDゲートの右下のORゲートは、ALUの検出されない永久故障と書かれており、SPFとDPFの確率を加算するためのORゲートです。
|
27 |
定量FTAによるPMHF計算法 |
昨日某社様向けにISO 26262ハードウェアセミナーを実施しましたが、以下のご質問を受けました。
Q「DPFを表すにはIFのフォールトの基事象とSMのフォールトの基事象をANDゲートで結べば良いが、定量FTAによりPMHFを表すには具体的にはどうすれば良いのでしょうか」
これは実務においては重要なノウハウとなります。その理由は規格ではPMHFの目標値がいくらで、それを満足しなければならないと書かれていますが、実際のECUでどのように計算するかにはほとんど言及が無いためです。わずかにPart 10に式が掲載されているに過ぎません。実は1st editionではいくつかの例が掲載されていましたが、2nd editionで削除されています。
結論から言えば、定量FTAでイベントの組み合わせでPMHF式を構築することになります。まず、1st editionに参考になるFT図が掲載されているので、これを子細に見てみます。
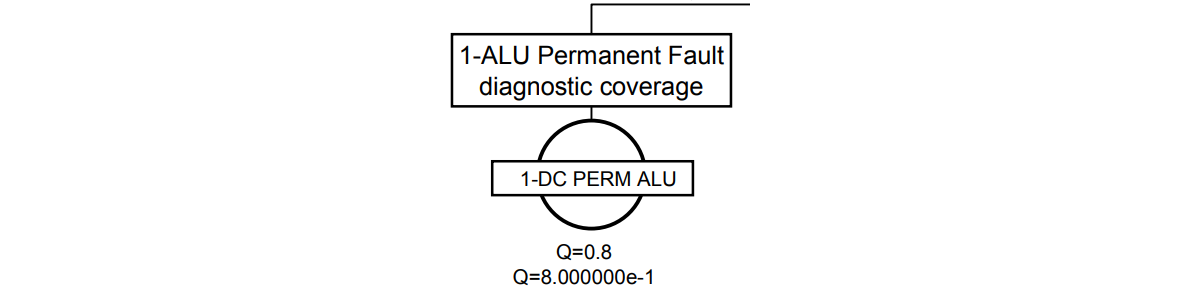
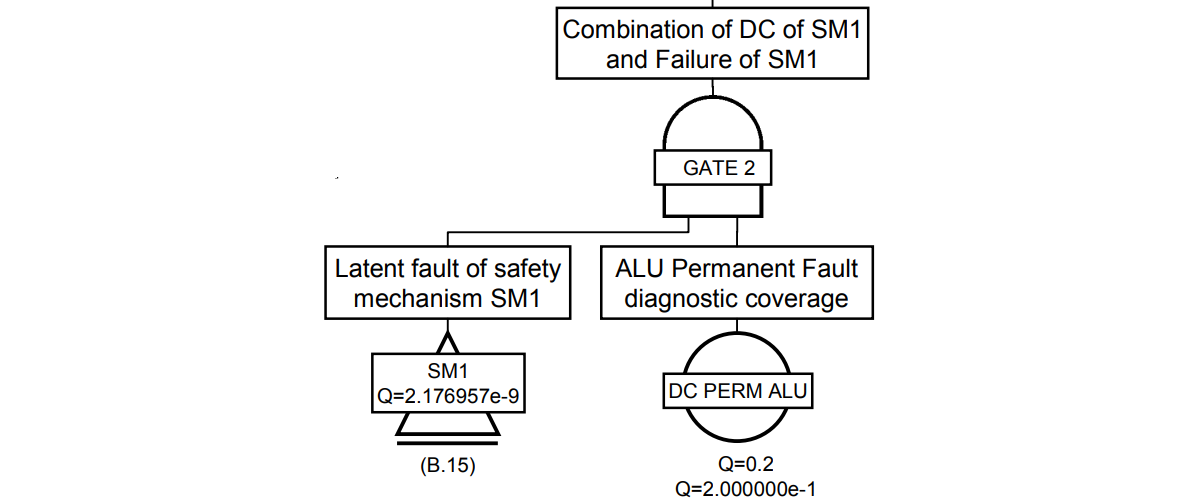
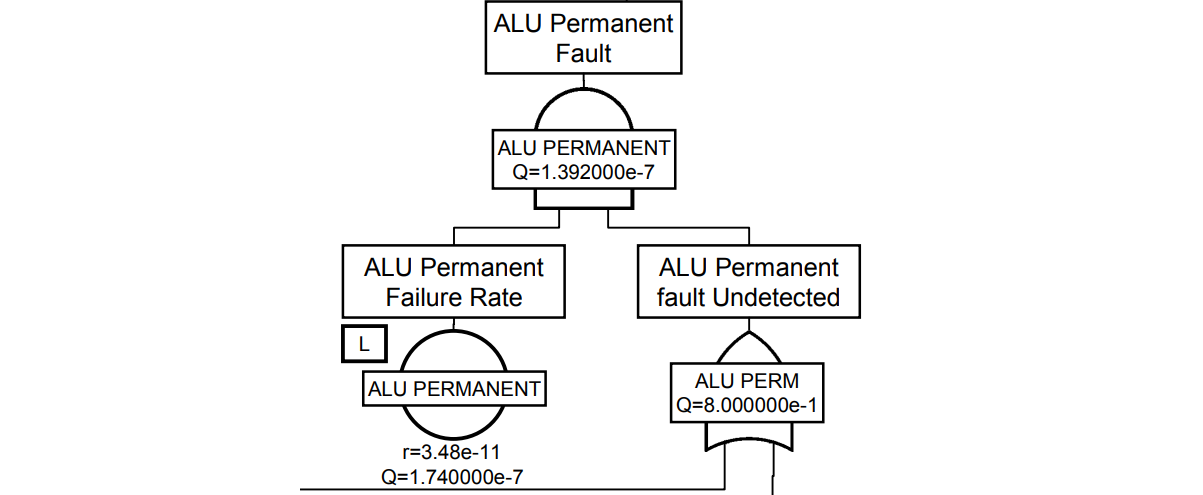
左のFT図はALUのフォールトのFTであり2つに分離していたものを組み合わせています。半分より上側のFTがちょうどSPF/RF項を、下側のFTがDPF項を表しています。FTツールではフォールトイベントを確率で表現するため、故障率には指定しなければミッションタイム$T$が自動でかかり、確率として表します。例外はLFの黄色で示すイベントで、ミッションタイムを手で入力し、$\tau$＝定期検査周期としています。
FTは確率$P$を表し、そのまま式で表すと①式となります。PMHF式は車両寿命においてSG侵害確率の時間平均であるため、①を$T$で割ると②の式となります。これはSM⇒IFの順にフォールトが起きる場合のPMHF式と1/2を除き一致します。さらにIF⇒SMの順のフォールトのPMHFを合わせると②となりますが、前提としてIFのフォールトもLFとなる必要があります。これは冗長を意味するものです。
記事の(10.1)に1st editionのPMHF式を掲載していますが、1/2を除き②と一致していることが確認されます。 $$ M_\text{PMHF} = \lambda_\text{RF}+\frac{1}{2}\lambda_\text{M,MPF}(\lambda_\text{SM,MPF,l}T_\text{lifetime}+ \lambda_\text{SM,MPF,d}\tau) \tag{10.1} $$ これをまとめたものをRAMS 2021に投稿し、採択されたので、以下に場所を示します。
https://ieeexplore.ieee.org/document/9605710
|
13 |
RAMS 2024採択へのマイルストーン |
次回のRAMS 2024(国際信頼性学会)は以下のように、2024/1/22～25に米国ニューメキシコ州アルバカーキで開催されます。
弊社代表は、IEEE学会に4年連続5回目(以下にリリース文を示す)の論文採択の実績がありますが、
RAMS(国際信頼性学会)としては5年連続5回目の採択を目指し、"Systematic Faults in the Derivation Process of the Probabilistic Failure Metric (PMHF) in ISO 26262"と題した論文を投稿予定であり、アブストラクトを作成中です。
対象となる論文は以下のブログ記事をまとめたものとなります。
本論文は、ISO 26262第2版解説書に示された、2nd editionにおけるPMHF式の導出過程を詳細に検討するものであり、結果として4種類11個もの、2nd editionのPMHF式の誤りを検出しています。
以下に例年通り、RAMS 2024採択へのマイルストーンを示します。
| 期限 | マイルストーン | 状態 |
|---|---|---|
| 2023/4/30 | アブストラクト投稿締め切り(名前、所属無し版) | |
| 2023/6/10 | アブストラクト採択結果 | |
| 2023/8/1 | 論文、プレゼン投稿締め切り(名前、所属無し版) | |
| 2023/9/1 | 第1回論文、プレゼン資料査読コメント受領 | |
| 2023/10/9 | 改訂版論文、プレゼン投稿締め切り(名前、所属無し版) | |
| 2023/10/22 | 最終査読コメント受領 | |
| 2023/10/10 | 学会出席登録締め切り | |
| 2023/10/10 | 最終論文、プレゼン投稿締め切り(名前、所属有り版) |
前のブログ