論理圧縮の実際
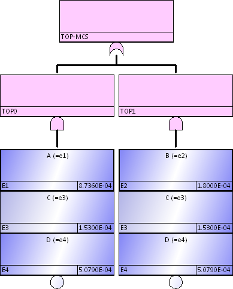
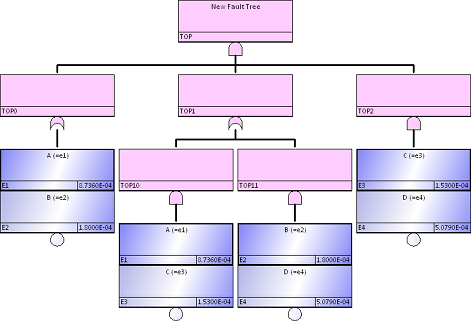
さらにツールを用いてやや複雑なFTに関して論理圧縮を実行してみましょう。英国Warwick大学のFTAの説明資料に以下のようなやや複雑なFTが例示されています。
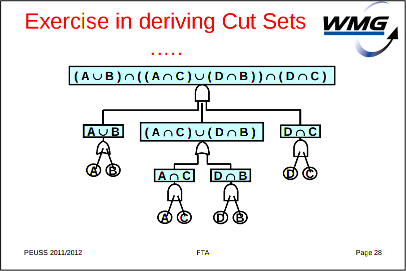 図25.1
図25.1これにFTA(4)のMCSアルゴリズムで示したブール代数により手作業で論理圧縮を実施すると、以下のようになります。
\[
(A\cup B)\cap((A\cap C)\cup(A\cap B))\cap(D\cap C)
=(A+B)(AC+DB)DC\\
=AACDC+ADBDC+BACDC+BDBDC\\
=ACD+ABCD+ABCD+BCD\\
=ACD(1+B)+BCD(1+A)\\
=ACD+BCD
\]
図25.2MCSは{{A, C, D}, {B, C, D}}と求められます。一方、WinCUPLで論理圧縮を行うには、以下のようなファイルを用意します。
Name MinimalCutSet;
PartNo 00 ;
Date 2016/03/28 ;
Revision 01 ;
Designer Engineer ;
Company FS Micro Corporation;
Assembly None ;
Location ;
Device ;
Pin [1..4] = [A, B, C, D];
Pin 5 = Q;
/* EQUATIONS */
Q.t = (A # B) & ((A & C) # (D & B)) & (D & C);
図25.3WinCUPLにより論理圧縮をかけた結果、以下のような出力が得られます。手作業で実施したのと同じ論理式が得られます。
*******************************************************************************
MinimalCutSet
*******************************************************************************
CUPL(WM) 5.0a Serial# 60008009
Device virtual Library DLIB-h-40-1
Created Tue Mar 29 09:37:27 2016
Name Minimal Cut Set
Partno 00
Revision 01
Date 2016/03/28
Designer Engineer
Company FS Micro Corporation
Assembly None
Location
===============================================================================
Expanded Product Terms
===============================================================================
Q.t =>
B & C & D
# A & C & D
図25.4MCSは同じく{{A, C, D}, {B, C, D}}と求められます。
 前のブログ
次のブログ
前のブログ
次のブログ