|
13 |
FTA (7) |
論理圧縮の実際
前回ご紹介した、英国Warwick大学のFTに対して、SAPHIREでTOP事象侵害確率を求めてみます。 FTのイベントに対して、$A=e_1$、$B=e_2$、$C=e_3$、$D=e_4$と置き直して、FTA(5)の表24.1のイベントの故障率に基づけば、
| 基事象ID | 故障率[FIT] |
|---|---|
| e1 | 8.74 |
| e2 | 1.80 |
| e3 | 1.53 |
| e4 | 5.08 |
これらに基づきSAPHIREでFTを構成すると図26-1のようになります。
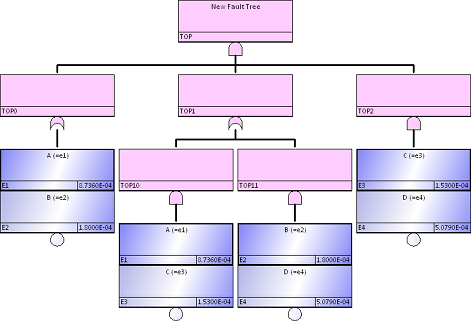
SAPHIREによりMCSを求め、TOP事象侵害確率を求めると以下の表のようになります。車両寿命を$10^5$時間とすれば、平均的な故障率は$8.186\cdot 10^{-6}[FIT]$となります。

MCSは同じく{{A, C, D}, {B, C, D}}と求められます。
