|
11 |
σ加法族と有限加法族 |
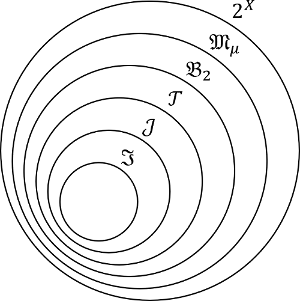
σ加法族と有限加法族を調べています。有限加法族にたいして無限和まで制約を厳しくしたものがσ加法族なので、有限加法族のほうが広い概念です。すなわち、
- σ加法族であれば有限加法族である。
- 有限加法族であっても σ加法族とは限らない。
そのため、有限加法族であっても σ加法族ではない例があるはずです。そこで、次の記事を参考にしました。https://sorai-note.com/math/algebra-of-sets/
Q 有限加法族であるが、σ加法族で無い例をひとつ挙げよ。
$\mathbb{N}$の部分集合からなる集合族 $$ \mathcal{F}=\left\{S\subseteq\mathbb{N}\mid Sまたは\overline{S}は有限集合\right\} $$ は$\mathbb{N}$上の有限加法族であることを示す。
- 空集合を含む:
空集合$\varnothing$は有限集合であるから$\varnothing\in\mathcal{F}$ - 補集合で閉じること:
$A\in\mathcal{F}$とすると、$\mathcal{F}$の定義より、$A$または$\overline{A}$のどちらかが有限集合。
(i) $A$が有限集合のとき
$\quad\overline{\overline{A}}$が有限集合なので、$\overline{A}\in\mathcal{F}$
(ii)$\overline{A}$が有限集合のとき
$\quad\mathcal{F}$の定義より、$\overline{A}\in\mathcal{F}$ - 有限和で閉じること:
$A, B\in\mathcal{F}$とする。$A$または$\overline{A}$のどちらかが有限集合であり、$B$または$\overline{B}$のどちらかが有限集合。
(i) $A$も$B$も有限集合のとき
$\quad A\cup B$が有限集合となるので、$A\cup B\in\mathcal{F}$である。
(ii)$\overline{A}$または$\overline{B}$が有限集合のとき
$\quad\overline{A}\cap\overline{B}$が有限集合、すなわち$\overline{A\cup B}$が有限集合なので、$A\cup B\in\mathcal{F}$である。
ここまでで$\mathcal{F}$は有限加法族であることが証明された。次に$\mathcal{F}$が加算和で閉じないことを示す。各$n\in\mathbb{N}$に対し、$A_n={2n}$とすると、これらは有限集合なので、$A_n\in\mathcal{F}$であるが、 $$ \bigcup_{n\in\mathbb{N}}A_n=\{2n\mid n\in\mathbb{N}\}=\{0, 2, 4, 6, ...\} $$ は無限集合であり、その補集合 $$ \overline{\bigcup_{n\in\mathbb{N}}A_n}=\{2n+1\mid n\in\mathbb{N}\}=\{1, 3, 5, 7, ...\} $$ も無限集合である。従って、$\bigcup_{n\in\mathbb{N}}A_n\notin\mathcal{F}$となる。