前回までに標本はどのようにとっても構わないことが分かったので、個々の部品の順列事象ではなく、故障の組み合わせ事象を、根元事象ととります。 ここでいう順列事象は$N=2$のときに、 $$\omega_1=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png}, \omega_2=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png}, \omega_3=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png}, \omega_4=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png}$$

組み合わせ事象は、 $$e_0=\omega_1, e_1=\{\omega_2, \omega_3\}, e_2=\omega_4$$ のようなものです。

コインの裏表のように等確率であれば、順列事象を根元事象ととる根拠もありますが、故障の場合はそうではなく、むしろ組み合わせ事象での故障数について、時間的な関係が存在します。

図195.1に、確率空間$(\Omega, \sigma(\Omega), P)$を図示します。根元事象を$\omega_i$と置きなおして、標本空間は$N$個の部品の故障数により分けた集合$\Omega$とします。具体的に書くと、 $$\omega_0=\{\img[-0.2em]{/images/up.png},...,\img[-0.2em]{/images/up.png}\},...,\omega_N=\{\img[-0.2em]{/images/dn.png},...,\img[-0.2em]{/images/dn.png}\}$$

事象空間$\mathcal{F}$は標本空間から生成した$\sigma$代数です。$\mathcal{F}$の中には$\Omega$の$N$個の根元事象1個ずつから成る$N$個の集合も$\mathcal{F}$に含まれ、それぞれの確率$P(\omega_i)$が存在しますが、我々が知りたいのは事象の確率ではなく、確率過程なので、事象の確率は気にしません。

$N$個の部品が同時に故障する確率は$0$なので、必ず一つずつ故障することから、上記根元事象は状態事象とも考えられます。つまり初期状態は$\omega_0$であり、ある時間後に1個故障した時点で、状態は$\omega_1$に移ります。図の矢印は状態遷移を意味した矢印です。連続時間マルコフ遷移となります。これは状態遷移は、それまでの状態の経過によらず、今いる状態(=故障数)と時間のみに関係するためです。

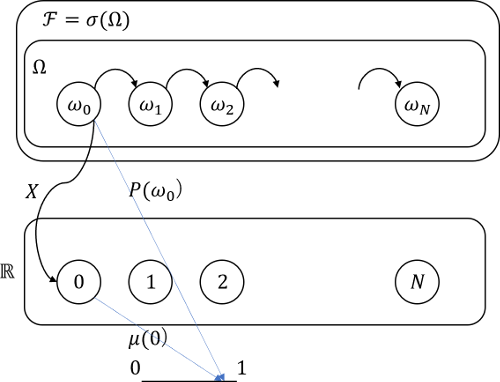
一方こちらは重要で、標本空間$\Omega$からボレル集合$\mathbb{R}$への写像である確率変数$X$は、$\omega\in\Omega$の故障数という定義であり、図195.1のように写像を行います。ただし、確率$P$は標本空間からユークリッド空間$[0, 1]$への写像であり、測度$\mu$はボレル集合$\mathbb{R}$からユークリッド空間$[0, 1]$への写像ですが、故障の観点からはどちらにもあまり興味がありません。なぜなら、それらの確率は$t$の増大につれて、順番に$P(\omega_i)=0$のものが$P(\omega_i)=1$となっていくからです。

故障時刻を$t_i(i=0,1,2,...)$とすれば、$t_0=0$として、 $$ P(\omega_i)= \begin{cases} 1 & ( t_i\leq t\lt t_{i+1} ) \\ 0 & ( \text{otherwise} ) \end{cases} $$

むしろ興味のある確率としては不信頼度です。$N$が非常に大きい場合、全体を1とする測度、つまり確率測度としての不信頼度は、故障数をNで割ったものです。システムの状態としては、$t=0$において$\omega_0$、その後$\omega_1, \omega_2, ...$と順番に遷移するので、確率変数$X$で状態変数を写像した$X(\omega_i)$を$N$で割ったものが不信頼度$F_X(t)$となります。その意味は、部品が$N$個ある場合に、時刻$t$までにおいて不稼働になる確率を表します。 $$F_X(t)=\frac{X(\omega, t)}{N}, R_X(t)=1-F_X(t)$$ そして、前記事のように、不信頼度についての確率微分方程式が故障率$\lambda$をパラメータとする制約条件として存在します。

前のブログ 次のブログ