|
30 |
Fault treeの自動生成 (7) |
 |
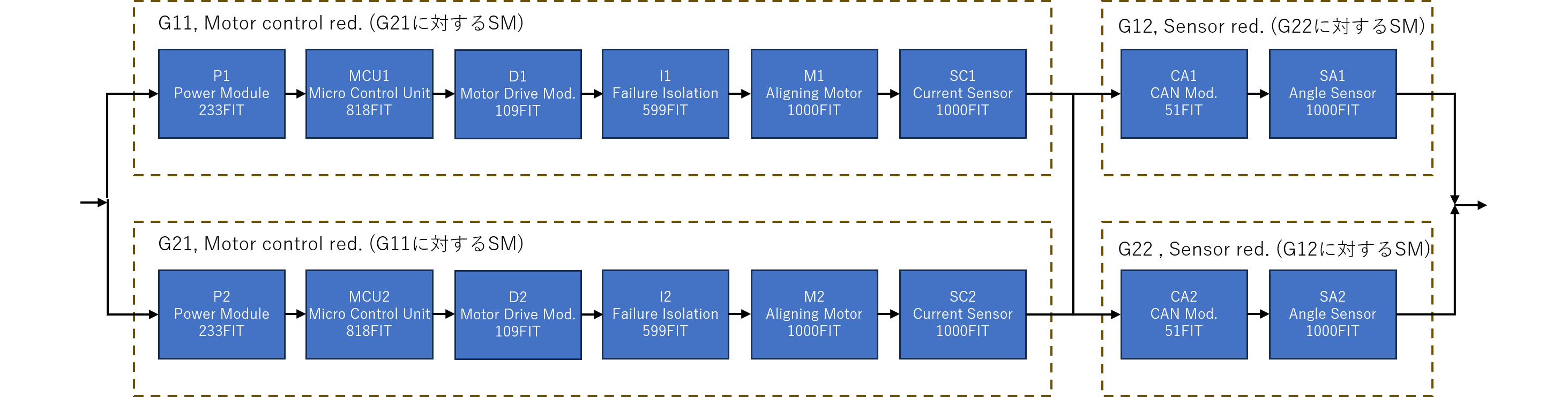
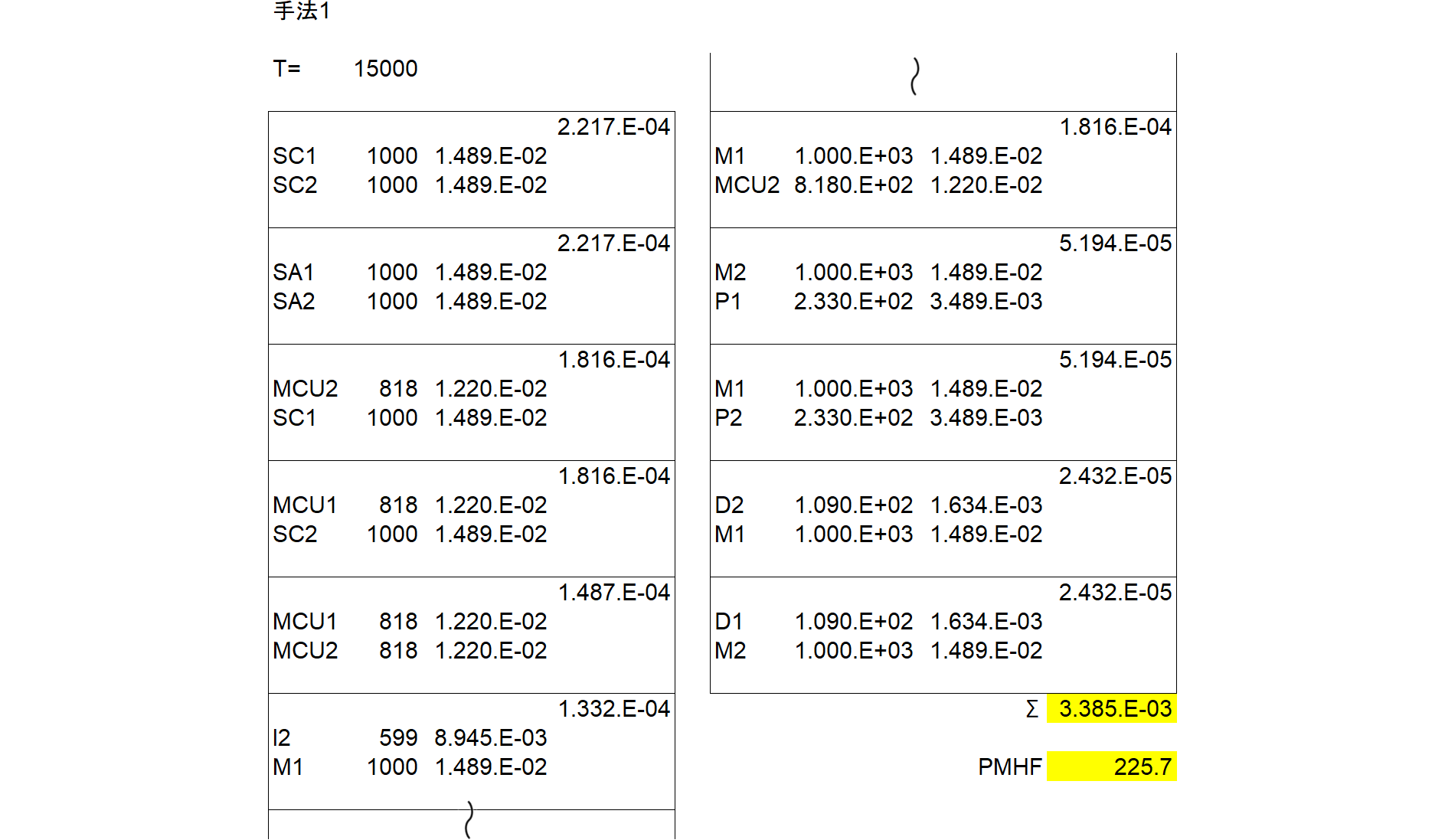
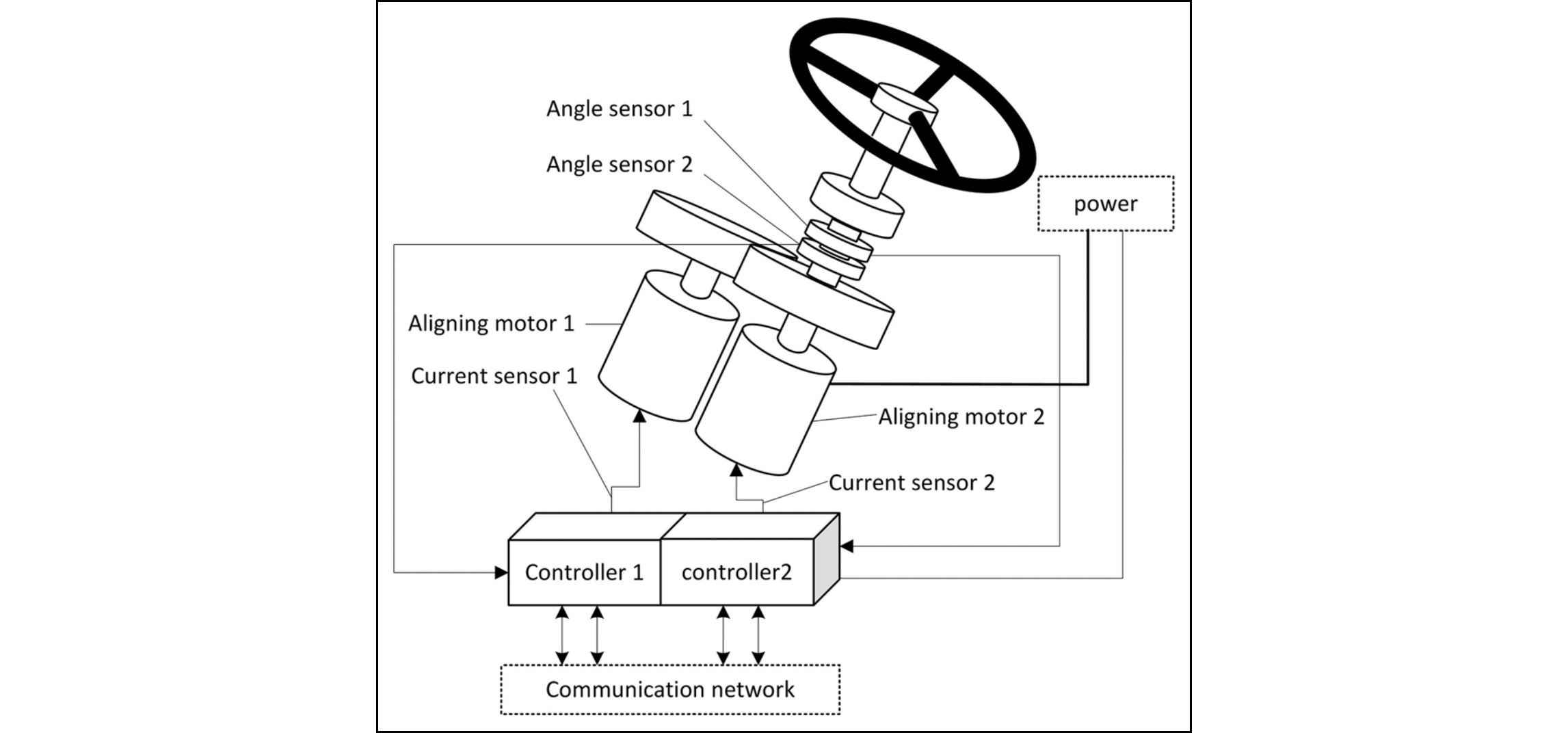
ChatGPTに前項のRBDを読ませ、頂上事象をMETHOD1としてMARDを生成してもらいました。それを示します。
METHOD1.MARD
TEST_Subs\METHOD1.BED
TEST_Subs\METHOD1.BEI
TEST_Subs\METHOD1.FTD
TEST_Subs\METHOD1.FTL
TEST_Subs\METHOD1.GTD
METHOD1.BED
*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
P1 ,P1desc ,TEST
MCU1 ,MCU1desc ,TEST
D1 ,D1desc ,TEST
I1 ,I1desc ,TEST
M1 ,M1desc ,TEST
SC1 ,SC1desc ,TEST
CA1 ,CA1desc ,TEST
SA1 ,SA1desc ,TEST
P2 ,P2desc ,TEST
MCU2 ,MCU2desc ,TEST
D2 ,D2desc ,TEST
I2 ,I2desc ,TEST
M2 ,M2desc ,TEST
SC2 ,SC2desc ,TEST
CA2 ,CA2desc ,TEST
SA2 ,SA2desc ,TEST
METHOD1.BEI
*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue,Prob,Lambda,Tau,Mission,Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
P1 ,3, , ,0.000E+000,0.000E+000,2.330E-007,0,1.500E+004, , ,0.000E+000,3.495E-003, ,RANDOM,CD,TEST
MCU1,3, , ,0.000E+000,0.000E+000,8.180E-007,0,1.500E+004, , ,0.000E+000,1.227E-002, ,RANDOM,CD,TEST
D1 ,3, , ,0.000E+000,0.000E+000,1.090E-007,0,1.500E+004, , ,0.000E+000,1.635E-003, ,RANDOM,CD,TEST
I1 ,3, , ,0.000E+000,0.000E+000,5.990E-007,0,1.500E+004, , ,0.000E+000,8.985E-003, ,RANDOM,CD,TEST
M1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
SC1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
CA1 ,3, , ,0.000E+000,0.000E+000,5.100E-008,0,1.500E+004, , ,0.000E+000,7.650E-004, ,RANDOM,CD,TEST
SA1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
P2 ,3, , ,0.000E+000,0.000E+000,2.330E-007,0,1.500E+004, , ,0.000E+000,3.495E-003, ,RANDOM,CD,TEST
MCU2,3, , ,0.000E+000,0.000E+000,8.180E-007,0,1.500E+004, , ,0.000E+000,1.227E-002, ,RANDOM,CD,TEST
D2 ,3, , ,0.000E+000,0.000E+000,1.090E-007,0,1.500E+004, , ,0.000E+000,1.635E-003, ,RANDOM,CD,TEST
I2 ,3, , ,0.000E+000,0.000E+000,5.990E-007,0,1.500E+004, , ,0.000E+000,8.985E-003, ,RANDOM,CD,TEST
M2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
SC2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
CA2 ,3, , ,0.000E+000,0.000E+000,5.100E-008,0,1.500E+004, , ,0.000E+000,7.650E-004, ,RANDOM,CD,TEST
SA2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
METHOD1.FTD
TEST =
* Name , Description, SubTree, Alternate, Project
METHOD1 ,Method1TopDef,, ,TEST
METHOD1.FTL
TEST,METHOD1 =
METHOD1 OR MCS01 MCS02 MCS03 MCS04 MCS05 MCS06 MCS07 MCS08 MCS09 MCS10 MCS11 MCS12 MCS13 MCS14 MCS15 MCS16 MCS17 MCS18 MCS19 MCS20 MCS21 MCS22 MCS23 MCS24 MCS25 MCS26 MCS27 MCS28 MCS29 MCS30 MCS31 MCS32 MCS33 MCS34 MCS35 MCS36 MCS37 MCS38 MCS39 MCS40
MCS01 AND P1 P2
MCS02 AND P1 MCU2
MCS03 AND P1 D2
MCS04 AND P1 I2
MCS05 AND P1 M2
MCS06 AND P1 SC2
MCS07 AND MCU1 P2
MCS08 AND MCU1 MCU2
MCS09 AND MCU1 D2
MCS10 AND MCU1 I2
MCS11 AND MCU1 M2
MCS12 AND MCU1 SC2
MCS13 AND D1 P2
MCS14 AND D1 MCU2
MCS15 AND D1 D2
MCS16 AND D1 I2
MCS17 AND D1 M2
MCS18 AND D1 SC2
MCS19 AND I1 P2
MCS20 AND I1 MCU2
MCS21 AND I1 D2
MCS22 AND I1 I2
MCS23 AND I1 M2
MCS24 AND I1 SC2
MCS25 AND M1 P2
MCS26 AND M1 MCU2
MCS27 AND M1 D2
MCS28 AND M1 I2
MCS29 AND M1 M2
MCS30 AND M1 SC2
MCS31 AND SC1 P2
MCS32 AND SC1 MCU2
MCS33 AND SC1 D2
MCS34 AND SC1 I2
MCS35 AND SC1 M2
MCS36 AND SC1 SC2
MCS37 AND CA1 CA2
MCS38 AND CA1 SA2
MCS39 AND SA1 CA2
MCS40 AND SA1 SA2
METHOD1.GTD
TEST=
* Name , Description, Project
METHOD1,Method1TopGate,,TEST
MCS01,PairP1P2,,TEST
MCS02,PairP1MCU2,,TEST
MCS03,PairP1D2,,TEST
MCS04,PairP1I2,,TEST
MCS05,PairP1M2,,TEST
MCS06,PairP1SC2,,TEST
MCS07,PairMCU1P2,,TEST
MCS08,PairMCU1MCU2,,TEST
MCS09,PairMCU1D2,,TEST
MCS10,PairMCU1I2,,TEST
MCS11,PairMCU1M2,,TEST
MCS12,PairMCU1SC2,,TEST
MCS13,PairD1P2,,TEST
MCS14,PairD1MCU2,,TEST
MCS15,PairD1D2,,TEST
MCS16,PairD1I2,,TEST
MCS17,PairD1M2,,TEST
MCS18,PairD1SC2,,TEST
MCS19,PairI1P2,,TEST
MCS20,PairI1MCU2,,TEST
MCS21,PairI1D2,,TEST
MCS22,PairI1I2,,TEST
MCS23,PairI1M2,,TEST
MCS24,PairI1SC2,,TEST
MCS25,PairM1P2,,TEST
MCS26,PairM1MCU2,,TEST
MCS27,PairM1D2,,TEST
MCS28,PairM1I2,,TEST
MCS29,PairM1M2,,TEST
MCS30,PairM1SC2,,TEST
MCS31,PairSC1P2,,TEST
MCS32,PairSC1MCU2,,TEST
MCS33,PairSC1D2,,TEST
MCS34,PairSC1I2,,TEST
MCS35,PairSC1M2,,TEST
MCS36,PairSC1SC2,,TEST
MCS37,PairCA1CA2,,TEST
MCS38,PairCA1SA2,,TEST
MCS39,PairSA1CA2,,TEST
MCS40,PairSA1SA2,,TEST
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。