|
18 |
Pongと強化学習 (59) |
 |
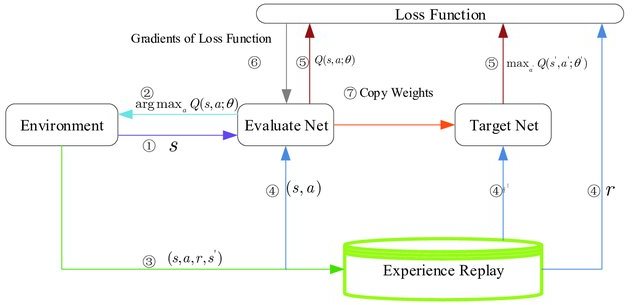
図867.1に基づき、5つのファンクションの間の関係を深掘りしてみます。まず環境とQ-networkとのインタフェースを聞いてみます。
強化学習における環境とQ-network間のインタフェースは、数学的な記号を用いて以下のように表現することができます。ここで、$Q(s, a; \theta)$は、パラメータ$\theta$を持つQ-networkによって推定される、状態$s$における行動$a$の期待される報酬(Q値)を表します。
環境からQ-networkへの出力
- 状態$s$: 環境は、現在の状態$s$をQ-networkに出力します。この状態は、例えばビデオゲームのフレームやセンサーからの読み取り値など、その時点での環境の状況を表す情報です。
Q-networkから環境への出力(間接的)
- 行動$a$: Q-networkは、入力された状態$s$に基づいて、各行動$a$に対するQ値、$Q(s, a; \theta)$を計算します。そして、ある方策(ポリシー)に従って、このQ値が最大となる行動$a^*$を選択します。この行動選択のプロセスは数学的には以下のように表現されます: $$ a^* = \arg\max_a Q(s, a; \theta) $$ 選択された行動$a^*$は、環境に適用され、環境の状態が更新されます。
学習プロセス
- 状態の更新と報酬の取得: エージェントが行動$a^*$を取った後、環境は新しい状態$s'$と即時報酬$r$をエージェントに提供します。また、エピソードが終了したかどうかを示すフラグ$done$も提供されます。
- DQNの損失関数の計算: 学習のため、DQNは以下の損失関数$L(\theta)$を使用して、パラメータ$\theta$を更新します。 $$ L(\theta) = \mathbb{E} \left[ \left( r + \gamma \max_{a'} Q(s', a'; \theta^-) - Q(s, a; \theta) \right)^2 \right] $$ ここで、$\theta^-$はターゲットQ-networkのパラメータ、$\gamma$は割引率です。
このプロセスを通じて、Q-network(エージェント)は環境との相互作用から学習し、最適な行動選択ポリシーを発達させていきます。