本年1月にUSのパームスプリングスで開催された、第67回国際信頼性学会のRAMS 2020に採択された論文は、半年後にようやくIEEE Xploreに掲載されました。しかしながら、学会側で原論文の体裁を編集したときに、式に誤りが混入したようで、一部の式に誤りがありました。

具体的には、図336.1のように式(9)が編集されていましたが、図336.1の1行目がおかしい部分で、確率式の後のカッコの意味が取れません。

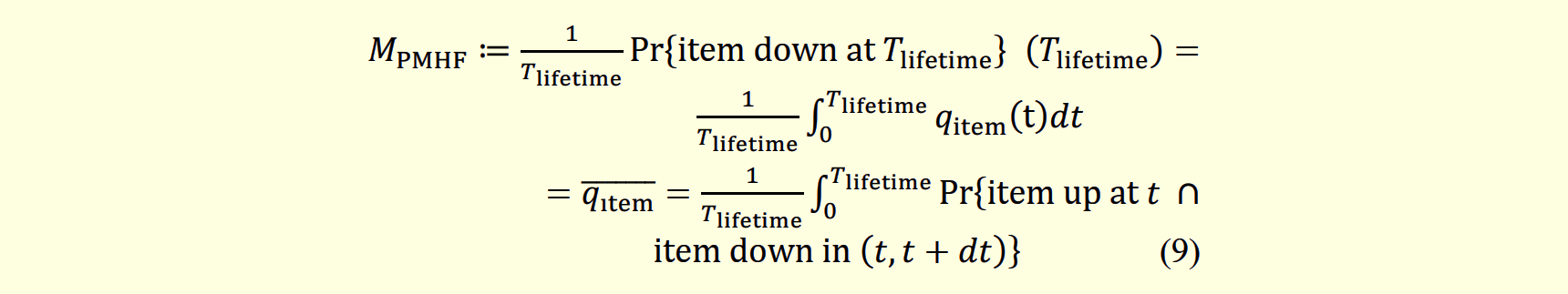
これに気づいたため、IEEE Xploreに連絡を取り、式(9)を原論文のものに戻してもらいました。IEEE Xploreに掲載されている論文に、以下のようにあまり見ない注が付けられているのは、このためのようです。

Notes: As originally published text, pages or figures in the document were missing or not clearly visible. A corrected replacement file was provided by the authors.

訳

注意: 元々公開されていたテキスト、文書内のページや図が欠落していたり、はっきりと見えなかったりしていたため、著者から訂正された差し替えファイルが提供された。

図336.2に原論文の式(9)を示します。黄色の部分が誤って削除されてしまった部分です。幸いこの他は原文どおりでした。

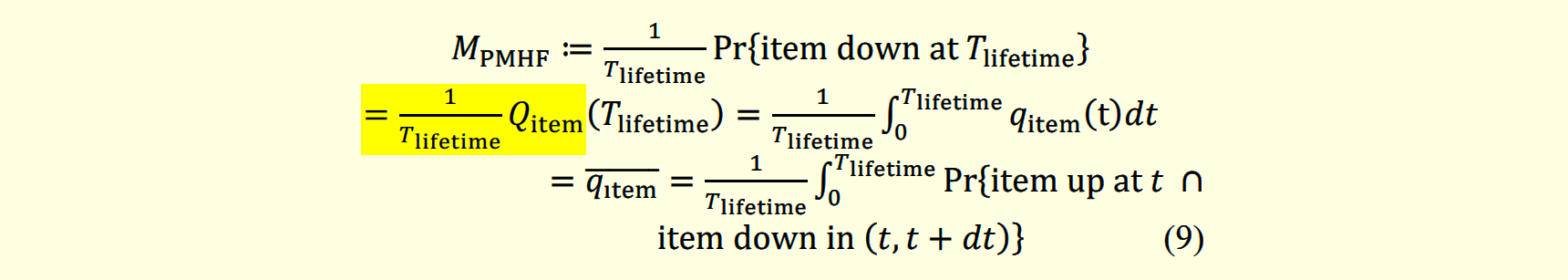
ちなみに、式の意味は各々以下のとおりです。

• 最初の等号: PMHFは車両寿命におけるアイテムのダウン確率の時間平均で定義されます(弊社の定義)。
• 次の等号: アイテムの時刻tにおけるダウン確率(PUA)を$Q(t)$とすると、車両寿命におけるアイテムのダウン確率は$Q(T_\text{lifetime})$で表されます。
• 次の等号: $Q(T_\text{lifetime})$はダウン確率密度(PUD)$q(t)$を0から車両寿命まで積分することで得られます。
• 次の等号: その時間平均とは平均ダウン確率密度(APUD)に他なりません。
• 次の等号: ダウン確率密度$q(t)$は、アイテムがtにおいて稼働(up)しており、かつその後の微小時間間隔$dt$中に不稼働(down)となる確率で表されます。

前のブログ 次のブログ