|
3 |
Fault treeの自動生成 (11) |
 |
Posts Tagged with "AI"
既に発行済みのブログであっても適宜修正・追加することがあります。We may make changes and additions to blogs already published.
 |
2 |
Fault treeの自動生成 (10) |
 |
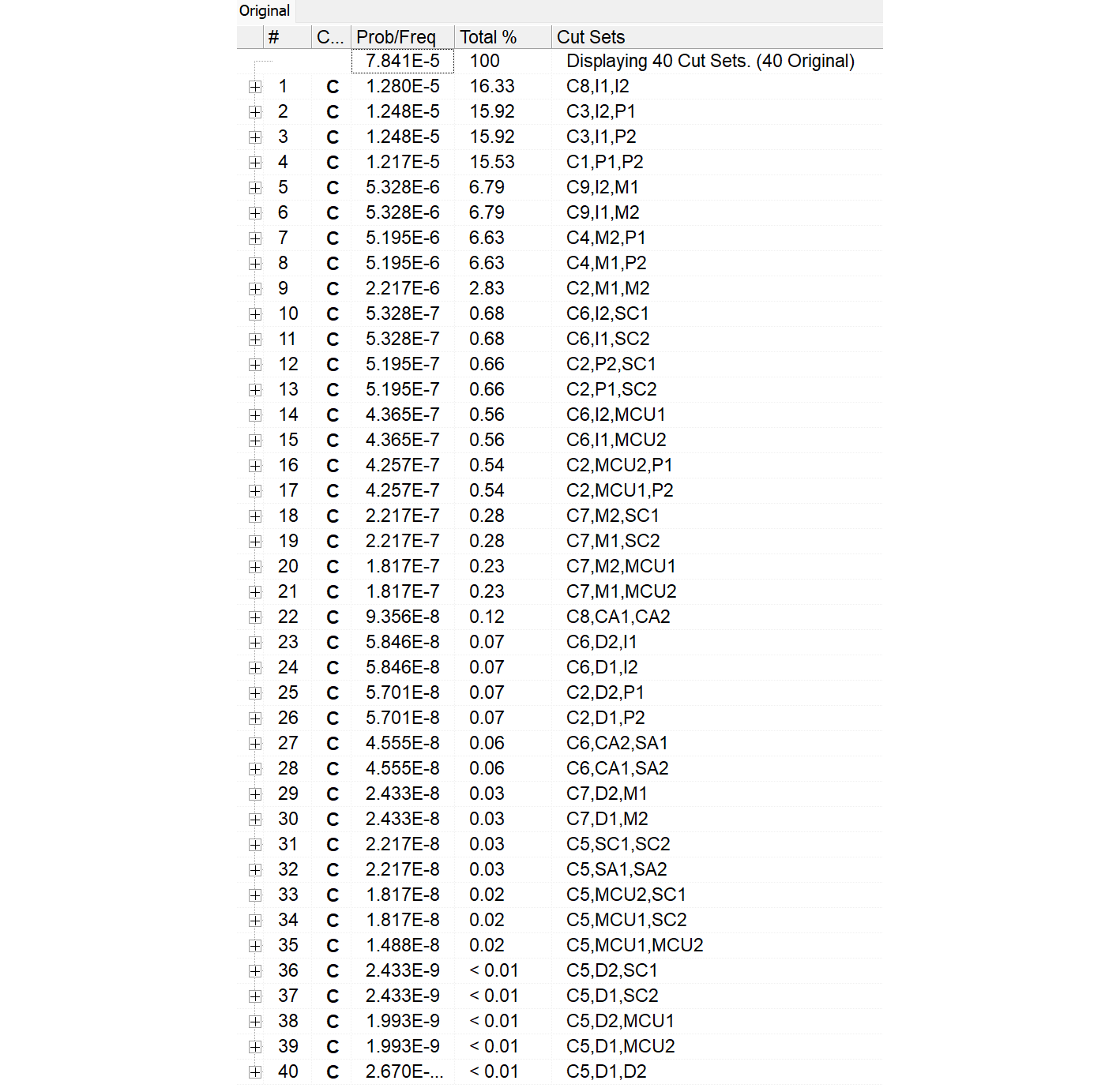
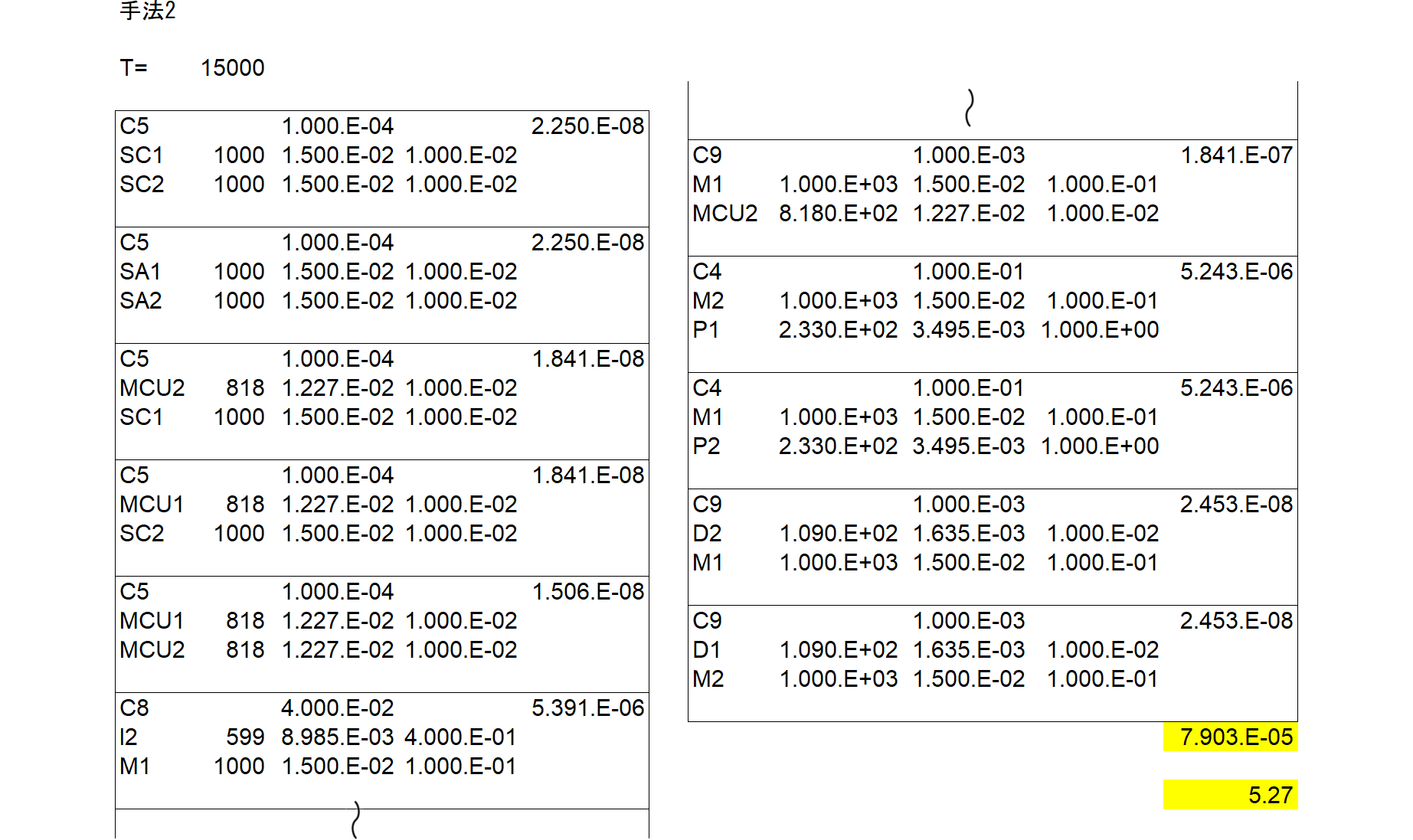
ChatGPTに前項のRBDを読ませ、頂上事象をMETHOD2としてMARDを生成してもらいました。2nd SMの効果の係数は再利用させ、40個になるところを9個としました。以下にMARDを示します。
METHOD2.MARD
TEST_Subs\METHOD2.BED
TEST_Subs\METHOD2.BEI
TEST_Subs\METHOD2.FTD
TEST_Subs\METHOD2.FTL
TEST_Subs\METHOD2.GTD
METHOD2.BED
*Saphire 8.2.9
TEST =
* Name, Descriptions, Project
P1, P1desc, TEST
MCU1, MCU1desc, TEST
D1, D1desc, TEST
I1, I1desc, TEST
M1, M1desc, TEST
SC1, SC1desc, TEST
CA1, CA1desc, TEST
SA1, SA1desc, TEST
P2, P2desc, TEST
MCU2, MCU2desc, TEST
D2, D2desc, TEST
I2, I2desc, TEST
M2, M2desc, TEST
SC2, SC2desc, TEST
CA2, CA2desc, TEST
SA2, SA2desc, TEST
C1, CoverageFactor_C1, TEST
C2, CoverageFactor_C2, TEST
C3, CoverageFactor_C3, TEST
C4, CoverageFactor_C4, TEST
C5, CoverageFactor_C5, TEST
C6, CoverageFactor_C6, TEST
C7, CoverageFactor_C7, TEST
C8, CoverageFactor_C8, TEST
C9, CoverageFactor_C9, TEST
METHOD2.BEI
*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue,Prob,Lambda,Tau,Mission,Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
P1 ,3, , ,0.000E+000,0.000E+000,2.330E-07,0,1.500E+004, , ,0.000E+000,3.489E-03, ,RANDOM,CD,TEST
MCU1 ,3, , ,0.000E+000,0.000E+000,8.180E-07,0,1.500E+004, , ,0.000E+000,1.220E-02, ,RANDOM,CD,TEST
D1 ,3, , ,0.000E+000,0.000E+000,1.090E-07,0,1.500E+004, , ,0.000E+000,1.634E-03, ,RANDOM,CD,TEST
I1 ,3, , ,0.000E+000,0.000E+000,5.990E-07,0,1.500E+004, , ,0.000E+000,8.945E-03, ,RANDOM,CD,TEST
M1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
SC1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
CA1 ,3, , ,0.000E+000,0.000E+000,5.100E-08,0,1.500E+004, , ,0.000E+000,7.647E-04, ,RANDOM,CD,TEST
SA1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
P2 ,3, , ,0.000E+000,0.000E+000,2.330E-07,0,1.500E+004, , ,0.000E+000,3.489E-03, ,RANDOM,CD,TEST
MCU2 ,3, , ,0.000E+000,0.000E+000,8.180E-07,0,1.500E+004, , ,0.000E+000,1.220E-02, ,RANDOM,CD,TEST
D2 ,3, , ,0.000E+000,0.000E+000,1.090E-07,0,1.500E+004, , ,0.000E+000,1.634E-03, ,RANDOM,CD,TEST
I2 ,3, , ,0.000E+000,0.000E+000,5.990E-07,0,1.500E+004, , ,0.000E+000,8.945E-03, ,RANDOM,CD,TEST
M2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
SC2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
CA2 ,3, , ,0.000E+000,0.000E+000,5.100E-08,0,1.500E+004, , ,0.000E+000,7.647E-04, ,RANDOM,CD,TEST
SA2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
C1 ,1, , ,0.000E+000,1.0000E+00,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E+00, ,RANDOM,CD,TEST
C2 ,1, , ,0.000E+000,1.0000E-02,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-02, ,RANDOM,CD,TEST
C3 ,1, , ,0.000E+000,4.0000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-01, ,RANDOM,CD,TEST
C4 ,1, , ,0.000E+000,1.0000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-01, ,RANDOM,CD,TEST
C5 ,1, , ,0.000E+000,1.0000E-04,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-04, ,RANDOM,CD,TEST
C6 ,1, , ,0.000E+000,4.0000E-03,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-03, ,RANDOM,CD,TEST
C7 ,1, , ,0.000E+000,1.0000E-03,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-03, ,RANDOM,CD,TEST
C8 ,1, , ,0.000E+000,1.6000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,1.6000E-01, ,RANDOM,CD,TEST
C9 ,1, , ,0.000E+000,4.0000E-02,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-02, ,RANDOM,CD,TEST
METHOD2.FTD
TEST =
* Name , Description, SubTree, Alternate, Project
METHOD2 ,Method2TopDefinition, , ,TEST
METHOD2.FTL
TEST,METHOD2 =
METHOD2 OR MCS01 MCS02 MCS03 MCS04 MCS05 MCS06 MCS07 MCS08 MCS09 MCS10 MCS11 MCS12 MCS13 MCS14 MCS15 MCS16 MCS17 MCS18 MCS19 MCS20 MCS21 MCS22 MCS23 MCS24 MCS25 MCS26 MCS27 MCS28 MCS29 MCS30 MCS31 MCS32 MCS33 MCS34 MCS35 MCS36 MCS37 MCS38 MCS39 MCS40
MCS01 AND P1 P2 C1
MCS02 AND P1 MCU2 C2
MCS03 AND P1 D2 C2
MCS04 AND P1 I2 C3
MCS05 AND P1 M2 C4
MCS06 AND P1 SC2 C2
MCS07 AND MCU1 P2 C2
MCS08 AND MCU1 MCU2 C5
MCS09 AND MCU1 D2 C5
MCS10 AND MCU1 I2 C6
MCS11 AND MCU1 M2 C7
MCS12 AND MCU1 SC2 C5
MCS13 AND D1 P2 C2
MCS14 AND D1 MCU2 C5
MCS15 AND D1 D2 C5
MCS16 AND D1 I2 C6
MCS17 AND D1 M2 C7
MCS18 AND D1 SC2 C5
MCS19 AND I1 P2 C3
MCS20 AND I1 MCU2 C6
MCS21 AND I1 D2 C6
MCS22 AND I1 I2 C8
MCS23 AND I1 M2 C9
MCS24 AND I1 SC2 C6
MCS25 AND M1 P2 C4
MCS26 AND M1 MCU2 C7
MCS27 AND M1 D2 C7
MCS28 AND M1 I2 C9
MCS29 AND M1 M2 C2
MCS30 AND M1 SC2 C7
MCS31 AND SC1 P2 C2
MCS32 AND SC1 MCU2 C5
MCS33 AND SC1 D2 C5
MCS34 AND SC1 I2 C6
MCS35 AND SC1 M2 C7
MCS36 AND SC1 SC2 C5
MCS37 AND CA1 CA2 C8
MCS38 AND CA1 SA2 C6
MCS39 AND SA1 CA2 C6
MCS40 AND SA1 SA2 C5
METHOD2.GTD
TEST=
* Name , Description, Project
METHOD2 ,Method2TopGate ,TEST
MCS01 ,Pair01, TEST
MCS02 ,Pair02, TEST
MCS03 ,Pair03, TEST
MCS04 ,Pair04, TEST
MCS05 ,Pair05, TEST
MCS06 ,Pair06, TEST
MCS07 ,Pair07, TEST
MCS08 ,Pair08, TEST
MCS09 ,Pair09, TEST
MCS10 ,Pair10, TEST
MCS11 ,Pair11, TEST
MCS12 ,Pair12, TEST
MCS13 ,Pair13, TEST
MCS14 ,Pair14, TEST
MCS15 ,Pair15, TEST
MCS16 ,Pair16, TEST
MCS17 ,Pair17, TEST
MCS18 ,Pair18, TEST
MCS19 ,Pair19, TEST
MCS20 ,Pair20, TEST
MCS21 ,Pair21, TEST
MCS22 ,Pair22, TEST
MCS23 ,Pair23, TEST
MCS24 ,Pair24, TEST
MCS25 ,Pair25, TEST
MCS26 ,Pair26, TEST
MCS27 ,Pair27, TEST
MCS28 ,Pair28, TEST
MCS29 ,Pair29, TEST
MCS30 ,Pair30, TEST
MCS31 ,Pair31, TEST
MCS32 ,Pair32, TEST
MCS33 ,Pair33, TEST
MCS34 ,Pair34, TEST
MCS35 ,Pair35, TEST
MCS36 ,Pair36, TEST
MCS37 ,Pair37, TEST
MCS38 ,Pair38, TEST
MCS39 ,Pair39, TEST
MCS40 ,Pair40, TEST
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。
 |
1 |
Fault treeの自動生成 (9) |
 |
 |
31 |
Fault treeの自動生成 (8) |
 |
SAPHIREでこれらのMARDファイルをロードすると、図918.1のようなFTが生成されます。

次にSolveで論理圧縮をかけ、View CutSetによりカットセットを表示させます。
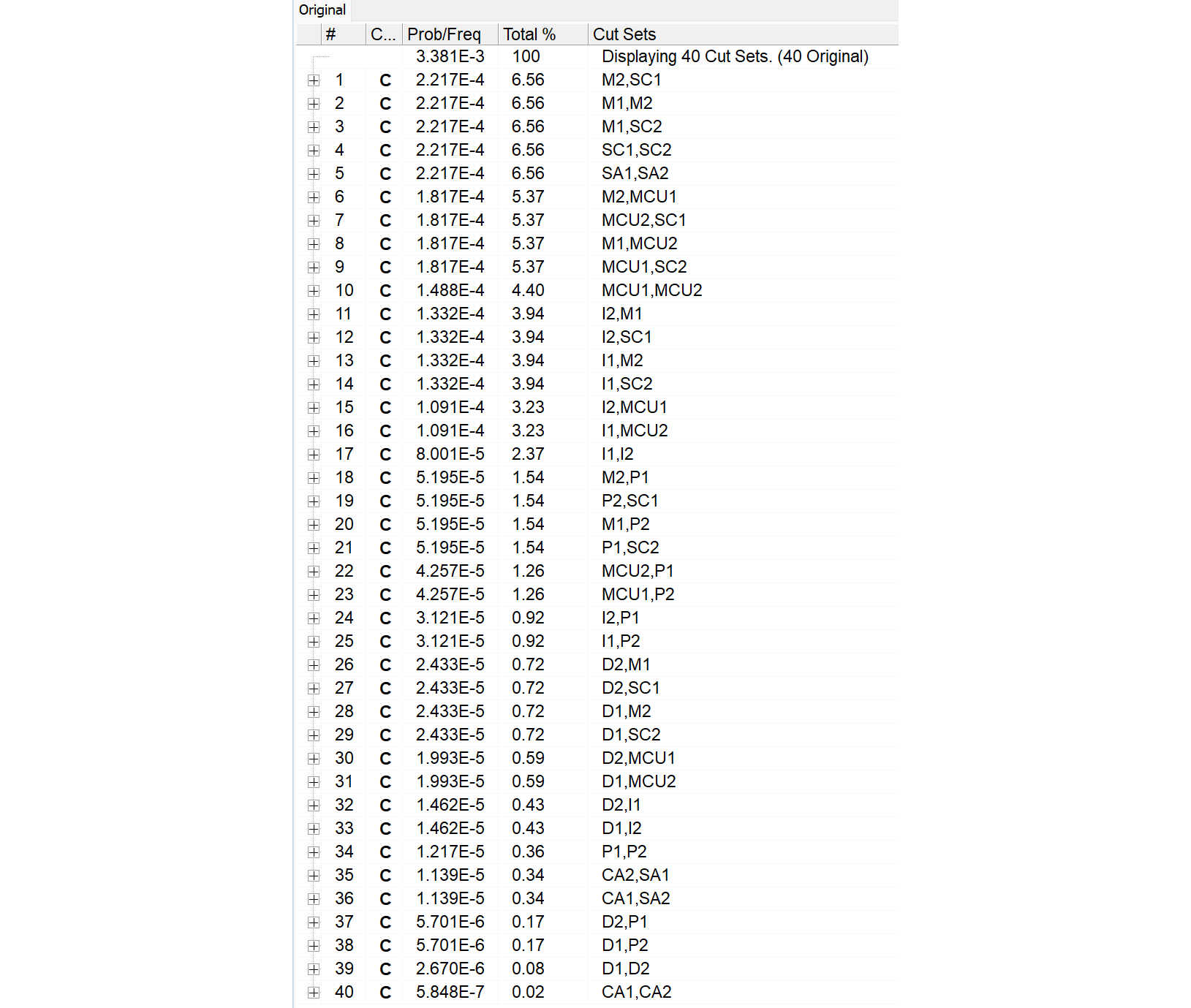
表918.1に示すとおり、頂上事象の確率は $\img[-1.35em]{/images/withinseminar.png}$ となります。
2020年にSaphireを使用した以前の記事では頂上事象の確率は3.380E-03でした。若干異なるのは丸め誤差や内部精度が変わったのかもしれません。
さらにExcelの結果である228.5 [FIT]と異なるのは、Excelは不信頼度を$\lambda T_\text{lifetime}$で計算しましたが、ツールはより正確な式である$1-e^{-\lambda T_\text{lifetime}}$で計算していることと丸め誤差の2つによるもののようです。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です。
 |
30 |
Fault treeの自動生成 (7) |
 |
ChatGPTに前項のRBDを読ませ、頂上事象をMETHOD1としてMARDを生成してもらいました。それを示します。
METHOD1.MARD
TEST_Subs\METHOD1.BED
TEST_Subs\METHOD1.BEI
TEST_Subs\METHOD1.FTD
TEST_Subs\METHOD1.FTL
TEST_Subs\METHOD1.GTD
METHOD1.BED
*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
P1 ,P1desc ,TEST
MCU1 ,MCU1desc ,TEST
D1 ,D1desc ,TEST
I1 ,I1desc ,TEST
M1 ,M1desc ,TEST
SC1 ,SC1desc ,TEST
CA1 ,CA1desc ,TEST
SA1 ,SA1desc ,TEST
P2 ,P2desc ,TEST
MCU2 ,MCU2desc ,TEST
D2 ,D2desc ,TEST
I2 ,I2desc ,TEST
M2 ,M2desc ,TEST
SC2 ,SC2desc ,TEST
CA2 ,CA2desc ,TEST
SA2 ,SA2desc ,TEST
METHOD1.BEI
*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue,Prob,Lambda,Tau,Mission,Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
P1 ,3, , ,0.000E+000,0.000E+000,2.330E-007,0,1.500E+004, , ,0.000E+000,3.495E-003, ,RANDOM,CD,TEST
MCU1,3, , ,0.000E+000,0.000E+000,8.180E-007,0,1.500E+004, , ,0.000E+000,1.227E-002, ,RANDOM,CD,TEST
D1 ,3, , ,0.000E+000,0.000E+000,1.090E-007,0,1.500E+004, , ,0.000E+000,1.635E-003, ,RANDOM,CD,TEST
I1 ,3, , ,0.000E+000,0.000E+000,5.990E-007,0,1.500E+004, , ,0.000E+000,8.985E-003, ,RANDOM,CD,TEST
M1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
SC1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
CA1 ,3, , ,0.000E+000,0.000E+000,5.100E-008,0,1.500E+004, , ,0.000E+000,7.650E-004, ,RANDOM,CD,TEST
SA1 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
P2 ,3, , ,0.000E+000,0.000E+000,2.330E-007,0,1.500E+004, , ,0.000E+000,3.495E-003, ,RANDOM,CD,TEST
MCU2,3, , ,0.000E+000,0.000E+000,8.180E-007,0,1.500E+004, , ,0.000E+000,1.227E-002, ,RANDOM,CD,TEST
D2 ,3, , ,0.000E+000,0.000E+000,1.090E-007,0,1.500E+004, , ,0.000E+000,1.635E-003, ,RANDOM,CD,TEST
I2 ,3, , ,0.000E+000,0.000E+000,5.990E-007,0,1.500E+004, , ,0.000E+000,8.985E-003, ,RANDOM,CD,TEST
M2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
SC2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
CA2 ,3, , ,0.000E+000,0.000E+000,5.100E-008,0,1.500E+004, , ,0.000E+000,7.650E-004, ,RANDOM,CD,TEST
SA2 ,3, , ,0.000E+000,0.000E+000,1.000E-006,0,1.500E+004, , ,0.000E+000,1.500E-002, ,RANDOM,CD,TEST
METHOD1.FTD
TEST =
* Name , Description, SubTree, Alternate, Project
METHOD1 ,Method1TopDef,, ,TEST
METHOD1.FTL
TEST,METHOD1 =
METHOD1 OR MCS01 MCS02 MCS03 MCS04 MCS05 MCS06 MCS07 MCS08 MCS09 MCS10 MCS11 MCS12 MCS13 MCS14 MCS15 MCS16 MCS17 MCS18 MCS19 MCS20 MCS21 MCS22 MCS23 MCS24 MCS25 MCS26 MCS27 MCS28 MCS29 MCS30 MCS31 MCS32 MCS33 MCS34 MCS35 MCS36 MCS37 MCS38 MCS39 MCS40
MCS01 AND P1 P2
MCS02 AND P1 MCU2
MCS03 AND P1 D2
MCS04 AND P1 I2
MCS05 AND P1 M2
MCS06 AND P1 SC2
MCS07 AND MCU1 P2
MCS08 AND MCU1 MCU2
MCS09 AND MCU1 D2
MCS10 AND MCU1 I2
MCS11 AND MCU1 M2
MCS12 AND MCU1 SC2
MCS13 AND D1 P2
MCS14 AND D1 MCU2
MCS15 AND D1 D2
MCS16 AND D1 I2
MCS17 AND D1 M2
MCS18 AND D1 SC2
MCS19 AND I1 P2
MCS20 AND I1 MCU2
MCS21 AND I1 D2
MCS22 AND I1 I2
MCS23 AND I1 M2
MCS24 AND I1 SC2
MCS25 AND M1 P2
MCS26 AND M1 MCU2
MCS27 AND M1 D2
MCS28 AND M1 I2
MCS29 AND M1 M2
MCS30 AND M1 SC2
MCS31 AND SC1 P2
MCS32 AND SC1 MCU2
MCS33 AND SC1 D2
MCS34 AND SC1 I2
MCS35 AND SC1 M2
MCS36 AND SC1 SC2
MCS37 AND CA1 CA2
MCS38 AND CA1 SA2
MCS39 AND SA1 CA2
MCS40 AND SA1 SA2
METHOD1.GTD
TEST=
* Name , Description, Project
METHOD1,Method1TopGate,,TEST
MCS01,PairP1P2,,TEST
MCS02,PairP1MCU2,,TEST
MCS03,PairP1D2,,TEST
MCS04,PairP1I2,,TEST
MCS05,PairP1M2,,TEST
MCS06,PairP1SC2,,TEST
MCS07,PairMCU1P2,,TEST
MCS08,PairMCU1MCU2,,TEST
MCS09,PairMCU1D2,,TEST
MCS10,PairMCU1I2,,TEST
MCS11,PairMCU1M2,,TEST
MCS12,PairMCU1SC2,,TEST
MCS13,PairD1P2,,TEST
MCS14,PairD1MCU2,,TEST
MCS15,PairD1D2,,TEST
MCS16,PairD1I2,,TEST
MCS17,PairD1M2,,TEST
MCS18,PairD1SC2,,TEST
MCS19,PairI1P2,,TEST
MCS20,PairI1MCU2,,TEST
MCS21,PairI1D2,,TEST
MCS22,PairI1I2,,TEST
MCS23,PairI1M2,,TEST
MCS24,PairI1SC2,,TEST
MCS25,PairM1P2,,TEST
MCS26,PairM1MCU2,,TEST
MCS27,PairM1D2,,TEST
MCS28,PairM1I2,,TEST
MCS29,PairM1M2,,TEST
MCS30,PairM1SC2,,TEST
MCS31,PairSC1P2,,TEST
MCS32,PairSC1MCU2,,TEST
MCS33,PairSC1D2,,TEST
MCS34,PairSC1I2,,TEST
MCS35,PairSC1M2,,TEST
MCS36,PairSC1SC2,,TEST
MCS37,PairCA1CA2,,TEST
MCS38,PairCA1SA2,,TEST
MCS39,PairSA1CA2,,TEST
MCS40,PairSA1SA2,,TEST
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。
 |
26 |
Fault treeの自動生成 (6) |
 |
RBD
順に手法1, 手法2, 手法3とFTを自動生成させます。入力はRBD(Reliability Block Diagram)です。まず冗長系EPSの2nd SM無しのモデル(手法1)を作成させます。
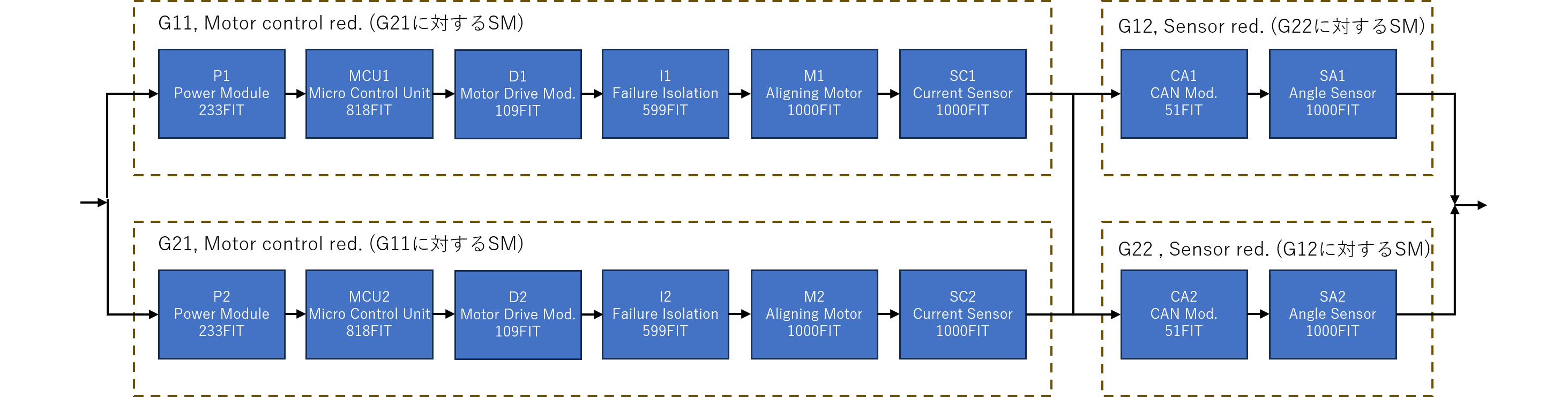
このMCSをとると、上流に関してチャネル1側とチャネル2側の個々の組み合わせが6x6=36通り、下流も同様に2x2=4通り、計40通りとなることが分かります。従ってあらかじめexcelにより正解値を求めておくと、図916.2のように、頂上侵害確率は3.428E-03、PMHFは228.5 [FIT]となります。
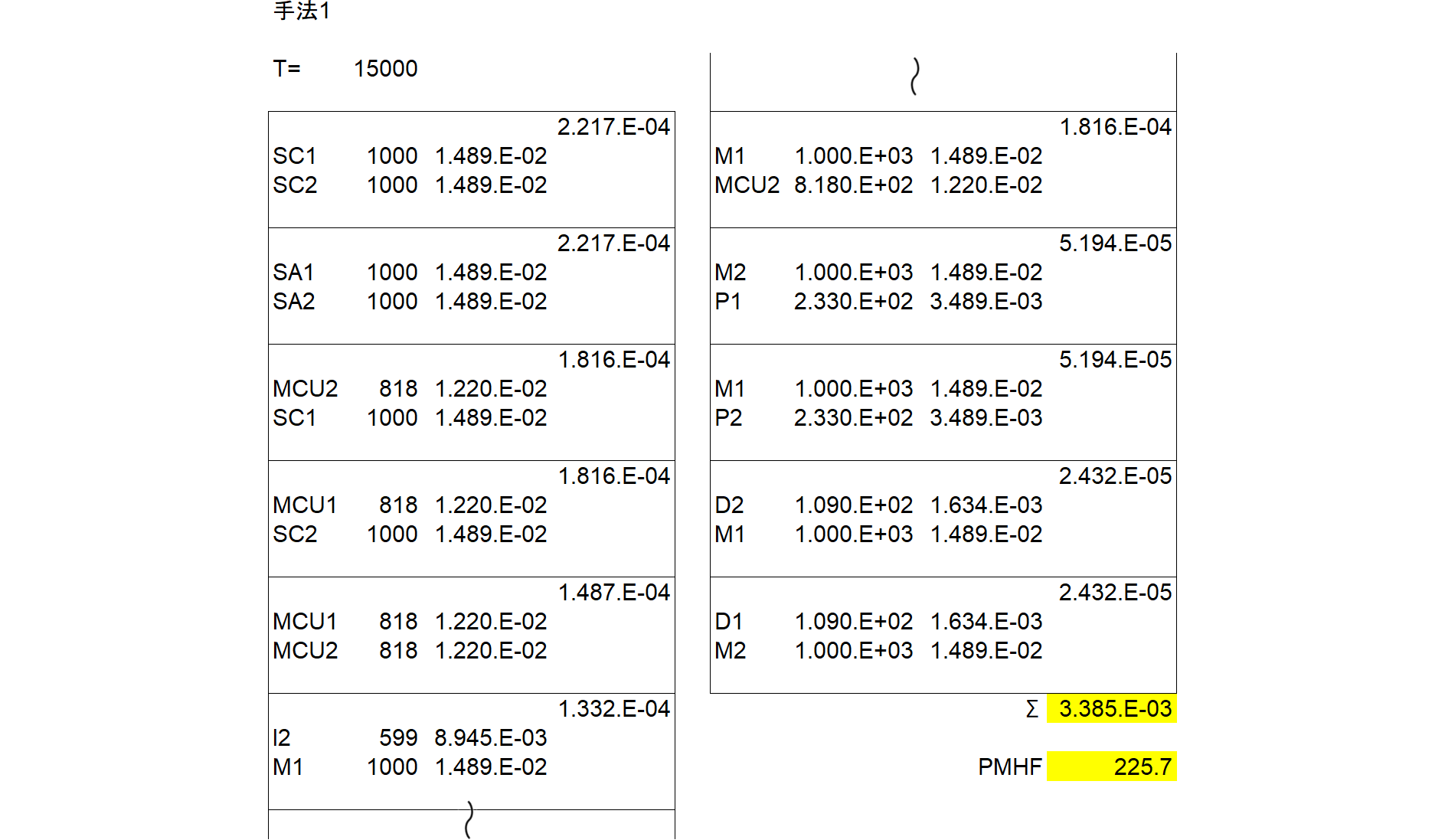
見方の例として、図の左上のSC1(チャネル1側エレメント)とSC2(チャネル2側エレメント)のペアを取ります。SC1とSC2において、それぞれ故障率は1000[FIT]、車両寿命間の不信頼度確率は1.500e-2、それらの積は2.250e-4となります。それらの40個の積項の和が頂上事象侵害確率であり、3.428e-3です。それを車両寿命で割るとPMHFが228.5[FIT]と算出できます。
このexcelによる結果を、検証のために正解値として保持しておきます。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です
 |
25 |
Fault treeの自動生成 (5) |
 |
理論背景
過去記事#213や過去記事#217で記載しましたが、冗長の場合のFT(fault tree)構築方式については以下の3通りが考えられます。
- 手法1: 2nd SM無しのFT
- 手法2: 2nd SM有りのFT
- 手法3: 規格式どおりの$\tau$の効果を入れたFT
弊社論文においては冗長系における2nd SMの効果まで書かれていませんでしたが、過去記事#217を参考にして、冗長の場合の不稼働確率を以下に示します。
$$ \begin{eqnarray} \Pr\{\text{TOP Unavailable}\}=M_\text{PMHF}\cdot T_\text{L}&=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L}) \img[-1.35em]{/images/withinseminar.png}\\ &=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L})C_\text{1, 2} \end{eqnarray} $$ ただし $$ K_\text{MPF}=1-(1-K_\text{E1,MPF})(1-K_\text{E2,MPF}) $$ $C_\text{1, 2}$はE1, E2に依存する定数で、 $$ C_\text{1, 2}\equiv \img[-1.35em]{/images/withinseminar.png} $$ ここで、上記のFT構成方法と対応させれば、
- 手法1: $C_\text{1, 2}=1$--- 2nd SMの効果無し、最悪見積もり
- 手法2: $C_\text{1, 2}=1-K_\text{MPF}=(1-K_\text{E1,MPF})(1-K_\text{E2,MPF})$---- 2nd SMの合成カバレージ分だけ故障率を減少させる
- 手法3: $C_\text{1, 2}=(1-K_\text{MPF})+K_\text{MPF}\cdot \frac{\tau}{T_\text{L}}$---- 2nd SMの合成カバレージ分だけ故障率を減少させるが、一方2nd SMの検査周期内は検査されないためDPFとなる確率が若干存在し、その分を補正する
ここで、ChatGPTからヒントを貰いました。手法2においてはこのように3 ANDを構成するのではなく、E1, E2の故障率をカバレージ残余で割り引けば良いとのこと。以下、これが成り立つことを証明します。
$$ \Pr\{\text{TOP Unavailable}\}=(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L})(1-K_\text{MPF})\\ =(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L})(1-K_\text{E1,MPF})(1-K_\text{E2,MPF})\\ =\left((1-K_\text{E1,MPF})\lambda_\text{E1}T_\text{L}\right) \left((1-K_\text{E2,MPF})\lambda_\text{E2}T_\text{L}\right)\quad(証明終) $$ このように手法2をとれば3 ANDにしなくても故障率を割り引くだけで済みますが、明示的に3 ANDにして2nd SMの効果を入れていることを表す方針とします。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です
 |
24 |
Fault treeの自動生成 (4) |
 |
過去記事ではFTを手で作成しました。その元となる論文を脚注$\dagger$に示します。ここでは生成AIで作成するトライアルを行います。
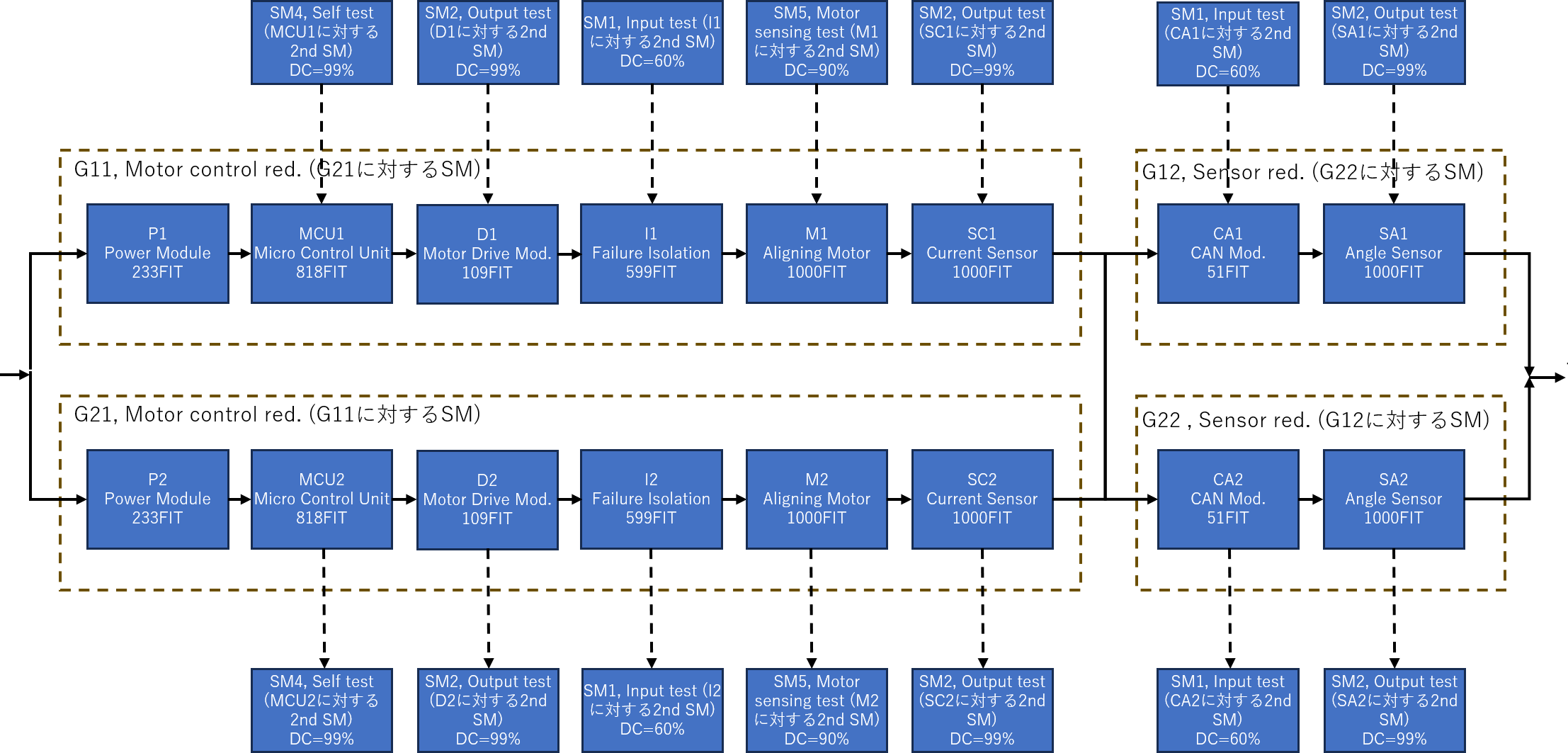
題材は完全冗長系のEPSです。なお本論文において車両寿命は15,000時間、2nd SMの検査時間は3,420時間とします(本来4,320時間=半年間のはずだが過去記事の誤り)。図914.1にEPSシステム構成図を示します。
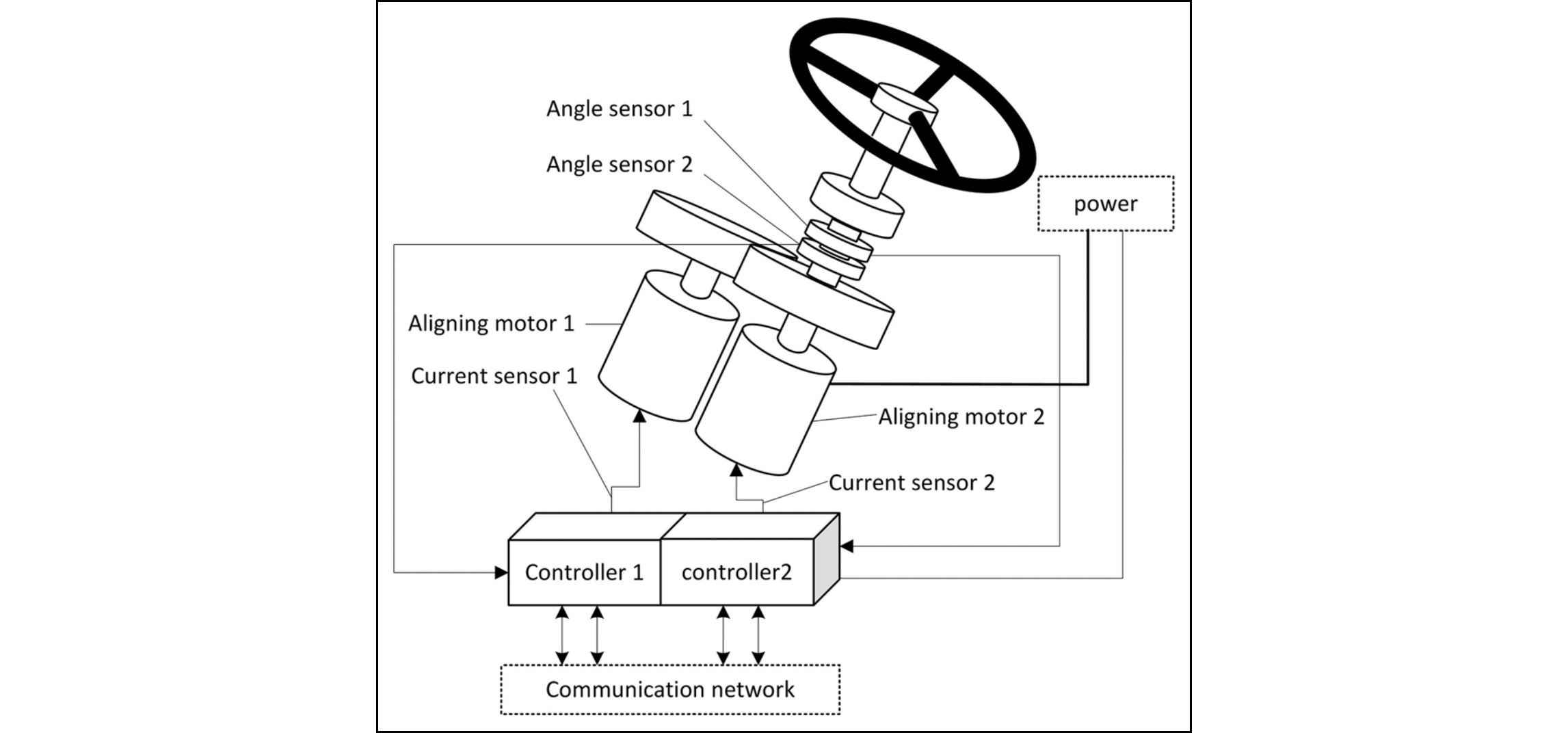
このEPSシステムのRBDを図914.2に示します。

表914.1にRBD中のエレメント記号とエレメント名等を示します。
| エレメント記号 | エレメント名 | 故障率[FIT] | SM記号 | SM名 | DC[%] |
|---|---|---|---|---|---|
| P | Power Module | 233 | None | None | 0 |
| MCU | Micro Control Unit | 818 | SM4 | Self test | 99 |
| D | Motor Drive Module | 109 | SM2 | Output test | 99 |
| I | Failure Isolation Module | 599 | SM1 | Input test | 60 |
| M | Aligning Motor | 1000 | SM5 | Motor sensing test | 90 |
| SC | Current Sensor | 1000 | SM2 | Output test | 99 |
| CA | CAN Communication Module | 51 | SM1 | Input test | 60 |
| SA | Angle Sensor | 1000 | SM3 | Sensor compare | 99 |
 |
28 |
Pongと強化学習 (81) |
 |
PongやBreakoutを観察すると、無駄にパドルが動いています。これはパドル動作にペナルティが無いためでしょうね。そのためにパドル動作(左移動、右移動)自体にペナルティを付加するにはどう改造したら良いですか?
Atariゲーム(例えばBreakoutやPong)においてパドルの動きにペナルティを付けることで、より効率的な動きを促すというアイデアは、特にエージェントが無駄な動きを減らすように学習するのに有効です。こうすることで、エージェントはより戦略的に行動を選択し、必要最小限の動きで最大の効果を達成しようとするでしょう。
ペナルティの実装方法
報酬関数の変更:
- ゲーム環境の報酬関数を変更して、特定の行動(この場合はパドルの左移動や右移動)が行われるたびに小さなペナルティ(例えば-0.01点)を与えます。
環境のカスタマイズ:
gymnasiumやAtari Learning Environment (ALE) を使用している場合、環境のソースコードに手を加える必要があるか、環境をラップするラッパークラスを作成して、報酬を操作します。
カスタム環境ラッパーの実装例
以下はPythonを使用してgymnasiumの環境にペナルティを適用する簡単な例です。この例では、gymnasiumラッパーを使用してBreakoutやPongの環境に介入し、パドルの動きに対してペナルティを適用します。
import gymnasium as gym
class PenalizePaddleMovement(gym.Wrapper):
def __init__(self, env, penalty=-0.01):
super(PenalizePaddleMovement, self).__init__(env)
self.penalty = penalty
self.last_action = None
def step(self, action):
observation, reward, done, info = self.env.step(action)
if action in [LEFT, RIGHT] and action == self.last_action: # 定義に基づく左右の行動
reward += self.penalty
self.last_action = action
return observation, reward, done, info
def reset(self, **kwargs):
self.last_action = None
return self.env.reset(**kwargs)
# 環境の作成とラッパーの適用
env = gym.make('Breakout-v0')
env = PenalizePaddleMovement(env)
# DQNや他の学習アルゴリズムで使用
このコードでは、PenalizePaddleMovementクラスが環境をラップし、パドルの連続した移動行動にペナルティを与える機能を追加しています。ここで、LEFTやRIGHTはゲーム固有の行動コードに置き換える必要があります。このペナルティは、同じ方向に連続してパドルを動かすときにのみ適用されます。
注意点
- ペナルティの値: ペナルティは非常に小さく設定することが重要です。これは、ペナルティが報酬を完全に打ち消さないようにするためです。
- 行動の定義:
LEFTやRIGHTといった具体的な行動は、使用している環境のAPIドキュメントを参照して適切な値に設定してください。 - 実験の検証: 変更を加えた後は、エージェントがまだ適切に学習できるかを確認するために、広範なテストが必要です。
この方法で、パドルの動きにペナルティを適用し、エージェントがより効率的な戦略を学習するよう促すことができます。
 |
27 |
Pongと強化学習 (80) |
 |
env = ClipRewardEnv(env)
env = gym.wrappers.ResizeObservation(env, (84, 84))
env = gym.wrappers.GrayScaleObservation(env)
env = gym.wrappers.FrameStack(env, 4)
を深掘りしてみます。
ご提示いただいたソースコードから、環境のラップ方法として複数の重要な変更が行われていることがわかります。これらは強化学習、特にDQNのようなアルゴリズムを用いる際に一般的に適用される変更です。それぞれのラッパーがどのような機能を果たしているかを以下に説明します。
1. ClipRewardEnv
このラッパーは環境から得られる報酬をクリップ(制限)します。多くの場合、報酬は+1, 0, -1のようにシンプルな形に変換されます。これにより、報酬のスケールが大きく異なる問題を防ぎ、学習プロセスを安定させることができます。
2. ResizeObservation
ResizeObservationラッパーは、環境から得られる観察(画像)を指定されたサイズ(この場合は84x84)にリサイズします。これにより、入力データの次元が減少し、計算負荷が軽減されると同時に、学習がより効率的に行えるようになります。
3. GrayScaleObservation
このラッパーは観察画像をグレースケールに変換します。カラー情報を削除することで、処理するデータ量をさらに削減し、重要な構造的情報にモデルが集中できるようにします。
4. FrameStack
FrameStackは連続する複数のフレーム(この場合は4フレーム)をスタックし、それを一つの観察として扱います。これにより、モデルは単一の画像からではなく、時間にわたる動きの情報を取得できるため、より複雑な環境のダイナミクスを学習することが可能になります。
5. env.action_space.seed(seed)
環境の行動空間にシードを設定して、再現性のあるランダム性を確保します。これは実験の一貫性を保つために重要です。
総合すると
これらのラッパーを組み合わせることで、学習アルゴリズムがより効率的かつ効果的に環境から学ぶことが可能になります。画像のサイズ変更、色の削減、報酬の正規化、そして時間的な情報の統合は、特に視覚的なデータを扱う場合において、モデルのパフォーマンスを大きく向上させることができます。このような準備を施すことで、ニューラルネットワークや他の機械学習モデルが、原始的なピクセルデータから有用な特徴を抽出しやすくなります。
ページ: