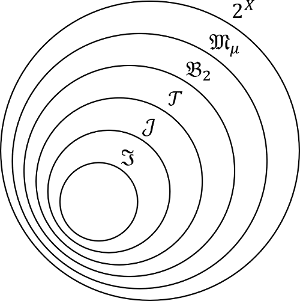
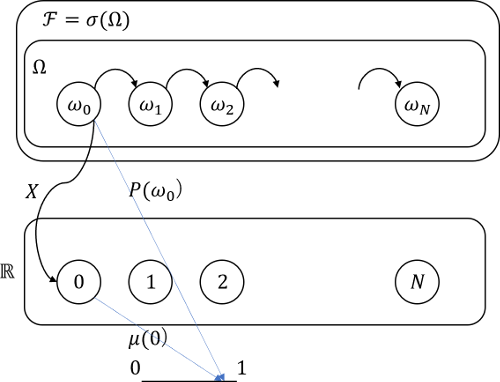
部分$\sigma$加法族の生成
また、Jupyter Notebookで生成された集合を見てみます。
まず、$N=2$のとき、根元事象を$\omega_i(i=1,...,4)$とすれば、確率変数$X$が故障数を表す場合の基本単位は、
$$\omega_1=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_2=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_3=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_4=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png}$$
のとき、
$$e_0=\omega_1, e_1=\{\omega_2, \omega_3\}, e_2=\omega_4$$
対応する故障数は、
$$X(e_0)=0, X(e_1)=1, X(e_2)=2$$
であり、この基本単位から生成される$\sigma$加法族$\mathcal{F}$は、数値を$\omega$のインデックスとして、
generate_sigma_algebra(FiniteSet(1,2,3,4), FiniteSet({1},{2,3},{4}))
F={∅,{1},{4},{1,4},{2,3},{1,2,3},{2,3,4},{1,2,3,4}}
len(generate_sigma_algebra(FiniteSet(1,2,3,4), FiniteSet({1},{2,3},{4})))
8
次に$N=3$のときは、根元事象を$\omega_i(i=1,...,8)$とすれば、確率変数$X$が故障数を表す場合の基本単位は、
$$\omega_1=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_2=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_3=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_4=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_5=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_6=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_7=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png},
\omega_8=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png}
$$
のとき、
$$e_0=\omega_1, e_1=\{\omega_2, \omega_3, \omega_4\}, e_2=\{\omega_5, \omega_6, \omega_7\}, e_3=\omega_8$$
対応する故障数は、
$$X(e_0)=0, X(e_1)=1, X(e_2)=2, X(e_3)=3$$
であり、この基本単位から生成される$\sigma$加法族は、数値を$\omega$のインデックスとして、
generate_sigma_algebra(FiniteSet(1,2,3,4,5,6,7,8), FiniteSet({1},{2,3,4},{5,6,7},{8}))
F={∅,{1},{8},{1,8},{2,3,4},{5,6,7},{1,2,3,4},{1,5,6,7},{2,3,4,8},{5,6,7,8},{1,2,3,4,8},{1,5,6,7,8},{2,3,4,5,6,7},{1,2,3,4,5,6,7},{2,3,4,5,6,7,8},{1,2,3,4,5,6,7,8}}
len(generate_sigma_algebra(FiniteSet(1,2,3,4,5,6,7,8), FiniteSet({1},{2,3,4},{5,6,7},{8})))
16
次に$N=4$のときは、根元事象を$\omega_i(i=1,...,16)$とすれば、確率変数$X$が故障数を表す場合の基本単位は、
$$\omega_1=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_2=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_3=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},
\omega_4=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_5=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_6=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png},\\
\omega_7=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_8=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_9=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_{10}=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_{11}=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png},\\
\omega_{12}=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png},
\omega_{13}=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png},
\omega_{14}=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png},
\omega_{15}=\img[-0.2em]{/images/up.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png},
\omega_{16}=\img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png} \img[-0.2em]{/images/dn.png},
$$
のとき、
$$e_0=\omega_1, e_1=\{\omega_2, \omega_3, \omega_4, \omega_5\}, e_2=\{\omega_6, \omega_7, \omega_8, \omega_9, \omega_{10}, \omega_{11}\}, e_3=\{\omega_{12}, \omega_{13}, \omega_{14}, \omega_{15}\}, e_4=\omega_{16}$$
対応する故障数は、
$$X(e_0)=0, X(e_1)=1, X(e_2)=2, X(e_3)=3, X(e_4)=4$$
であり、この基本単位から生成される$\sigma$加法族は、数値を$\omega$のインデックスとして、
generate_sigma_algebra(FiniteSet(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16), FiniteSet({1},{2,3,4,5},{6,7,8,9,10,11},{12,13,14,15},{16}))
F={∅,{1},{16},{1,16},{2,3,4,5},{12,13,14,15},{1,2,3,4,5},{1,12,13,14,15},{2,3,4,5,16},{12,13,14,15,16},{1,2,3,4,5,16},{1,12,13,14,15,16},{6,7,8,9,10,11},{1,6,7,8,9,10,11},{6,7,8,9,10,11,16},{1,6,7,8,9,10,11,16},{2,3,4,5,12,13,14,15},{1,2,3,4,5,12,13,14,15},{2,3,4,5,12,13,14,15,16},{1,2,3,4,5,12,13,14,15,16},{2,3,4,5,6,7,8,9,10,11},{6,7,8,9,10,11,12,13,14,15},{1,2,3,4,5,6,7,8,9,10,11},{1,6,7,8,9,10,11,12,13,14,15},{2,3,4,5,6,7,8,9,10,11,16},{6,7,8,9,10,11,12,13,14,15,16},{1,2,3,4,5,6,7,8,9,10,11,16},{1,6,7,8,9,10,11,12,13,14,15,16},{2,3,4,5,6,7,8,9,10,11,12,13,14,15},{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16},{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}}
len(generate_sigma_algebra(FiniteSet(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16), FiniteSet({1},{2,3,4,5},{6,7,8,9,10,11},{12,13,14,15},{16})))
32
部品が$N$個ある場合の基本単位数は$N+1$となり、部分$\sigma$加法族の要素数は$2^{N+1}=2\cdot 2^N$となります。
 前のブログ
次のブログ
前のブログ
次のブログ