|
10 |
Kパラメータは条件付き確率か (2) |
(98.1)の定義を用いれば、時刻$t$から$t+dt$において発生するIFのフォールトについて、VSG抑止される確率を求めると、条件付き確率のチェインルールを用いれば、 $$ \Pr\{\mathrm{IF\ prevented}\cap\mathrm{IF\ failed\ in\ }(t, t+dt]\cap\mathrm{IF\ not\ failed\ before\ }t\}\\ =\Pr\{\mathrm{IF\ prevented}\ |\ \mathrm{IF\ failed\ in\ }(t, t+dt]\cap\mathrm{IF\ not\ failed\ before\ }t\}\\ \cdot\Pr\{\mathrm{IF\ failed\ in\ }(t, t+dt]\ |\ \mathrm{IF\ not\ failed\ before\ }t\}\cdot\Pr\{\mathrm{IF\ not\ failed\ before\ }t\}\tag{99.1} $$ ここで、それぞれ $$ \Pr\{\mathrm{IF\ prevented}\ |\ \mathrm{IF\ failed\ in\ }(t, t+dt]\cap\mathrm{IF\ not\ failed\ before\ }t\}=K_{\mathrm{IF,FMC,RF}},\\ \Pr\{\mathrm{IF\ failed\ in\ }(t, t+dt]\ |\ \mathrm{IF\ not\ failed\ before\ }t\}=\lambda_{\mathrm{IF}}dt,\\ \Pr\{\mathrm{IF\ not\ failed\ before\ }t\}=R_{\mathrm{IF}}(t) \tag{99.2} $$ であるから、 $$ (99.1)=K_{\mathrm{IF,FMC,RF}}\lambda_{\mathrm{IF}}R_{\mathrm{IF}}(t)dt\tag{99.3} $$ と、IFに関する故障率や信頼度関数で表すことができます。
問題1
しかしながら、Kパラメータ($K_{\mathrm{FMC,MPF}}$及び$K_{\mathrm{FMC,RF}}$)が条件付き確率として一定だと矛盾が起きます。抑止条件が確率的に作用することにより、例えば1回目にはVSG抑止されたフォールトが、2回目にはVSG抑止されないことが起こりえます。あるいは1回目にはリペアされたフォールトが2回目にはリペアされないことが起こりえます。検出が確率的になされるからとはいえ、同じ故障が検出されたりされなかったりするのは、合理性がありません。
問題2
次に、例えば故障検出率$K_{\mathrm{FMC,MPF}}$について考えると、長時間が経ち故障検出を長く続ける場合を考えます。検出されるフォールトは全量リペアされるのに比べて、検出されないフォールトはどんどん溜まって行き、不信頼度は上昇し続けます。従って、新たにフォールトするうちの検出される部分の比率が高まりそうであるのに、条件付き確率として一定値であると感覚に反します。
フォールト検出のたびにサイコロで検出を決めているならそのようになりますが、一般的には診断カバレージ(Diagnostic Coverage; DC)はSMのアーキテクチャにより決定され、確率的には検出されないとここでは考えることにします。そうすれば、上記の問題点は解消されます。
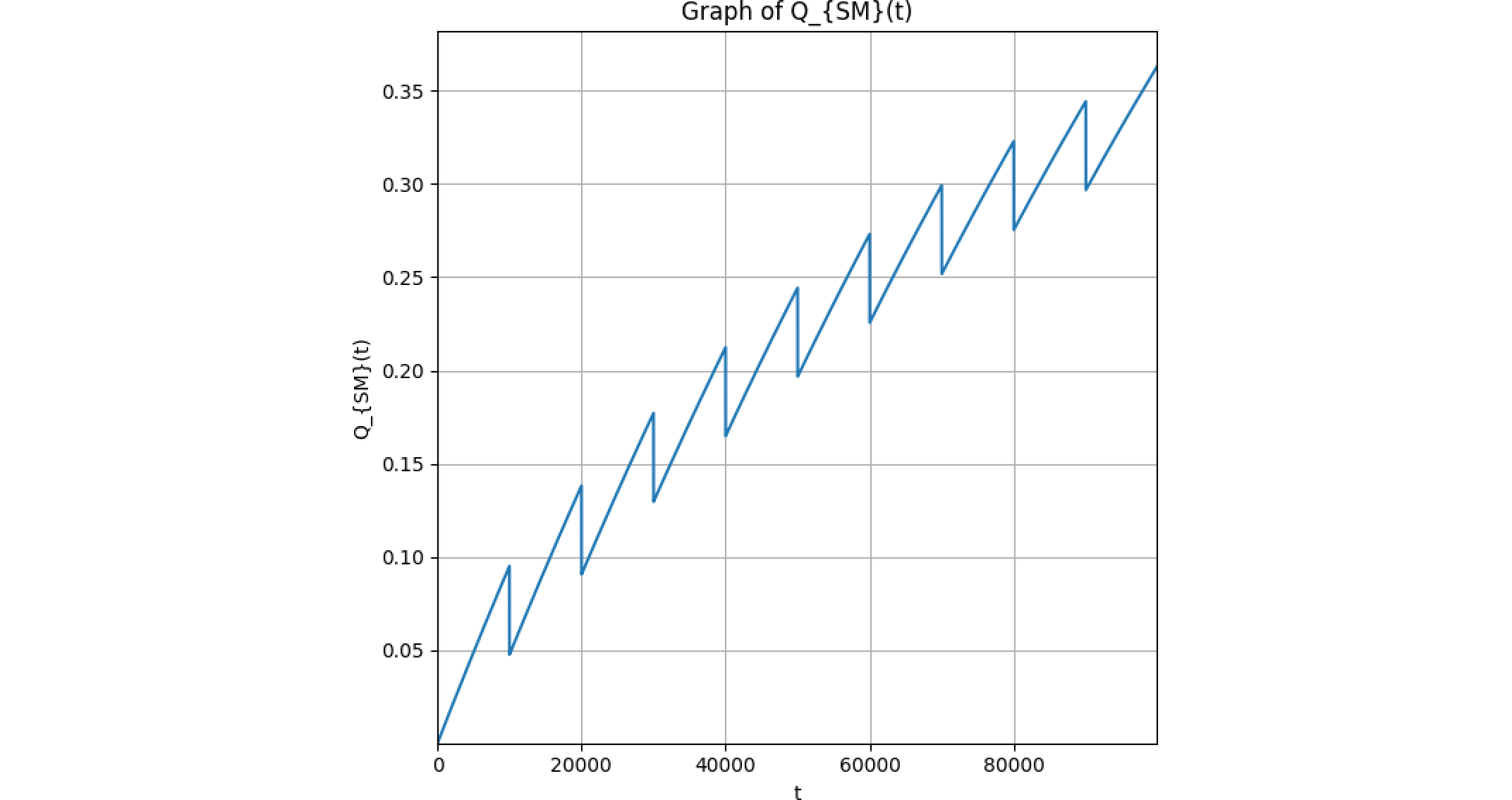
問題1
確率的に一定ではなく、アーキテクチャ的に一定量を必ず検出できるとした場合のグラフです。これであれば、$\tau$毎に必ず検出分は修理され、問題はありません。
問題2
これに関しても、アーキテクチャ的に一定量を必ず検出できるとした場合、グラフから見られるように、不信頼度は時間と伴に上昇していきます。

Leave a Comment