|
1 |
新方式によるPUDの導出 |
過去記事のPUAのグラフの続きです。
過去記事において、新方式$\dagger$による正確なPUA(758.4)である$Q_{\text{exact},n}(t)$を導出しましたが、本稿では正確なPUDである$q_{\text{exact},n}(t)$を導出します。これは $$ q_{\text{exact},n}(t)=\frac{dQ_{\text{exact},n}(t)}{dt} $$ であるため、過去記事におけるPUA(758.4)を時間微分するだけです(ただし、微分不可能な時刻$t=i\tau, i=1, 2, 3...$を除く)。従って、正確なPUDは、 $$ q_{\text{exact},n}(t)=f(t)+\img[-1.35em]{/images/withinseminar.png},\\ t\notin \{i\tau; i=1, 2, 3,...,n\},\ n=\lfloor t/\tau\rfloor\ge1\tag{766.1} $$ 一方、近似PUDは、同様に近似PUA(759.2)である$Q_\text{approx}(t)$を時間微分して、 $$ q_\text{approx}(t)=\frac{dQ_\text{approx}(t)}{dt}=(1-K_\text{MPF})f(t)+K_\text{MPF}f(u),\\ \ u=t\bmod\tau,\ t\notin \{i\tau; i=1, 2, 3,...,n\},\ n=\lfloor t/\tau\rfloor\tag{766.2} $$
正確なPUD及び近似PUDのグラフの$\lambda=0.1$、$0.01$、$0.001$の3例をChatGPTに書かせてみます。
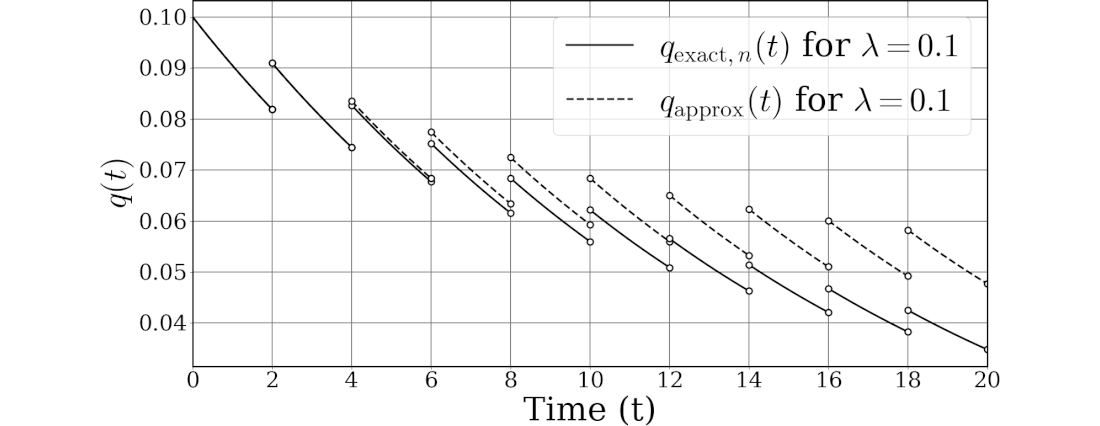
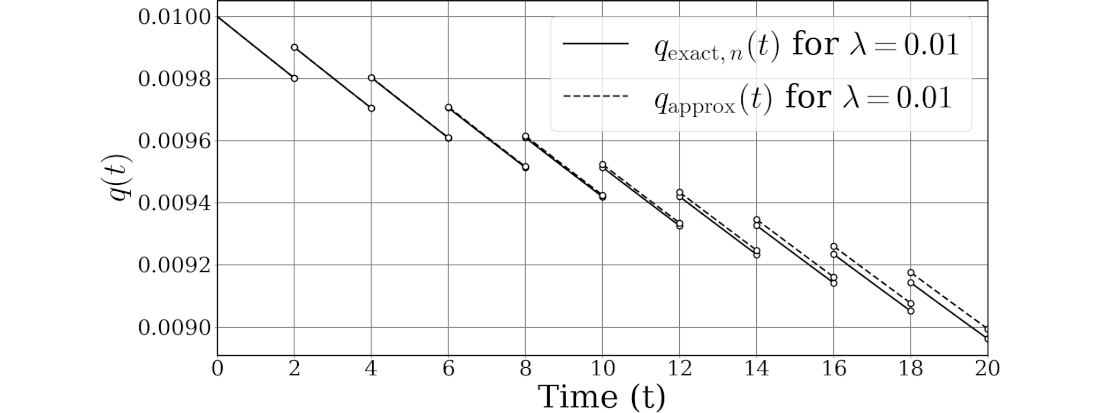
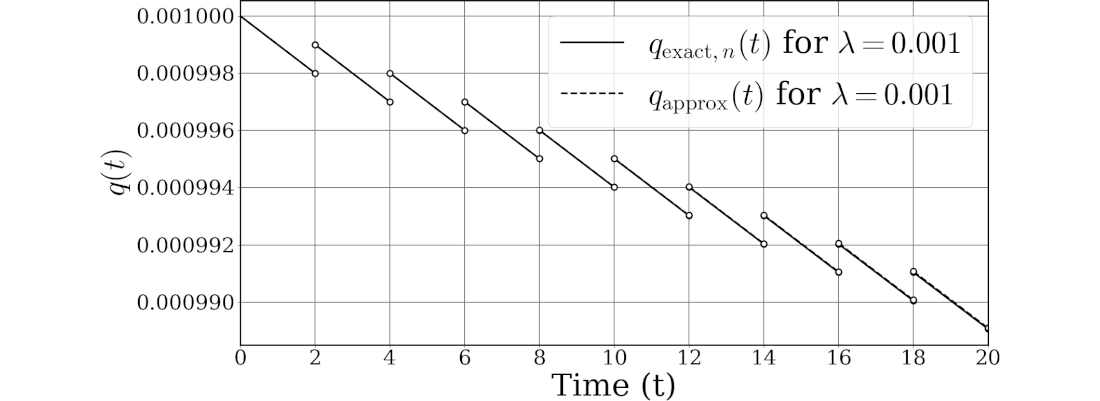
PUDもPUAと同様に$\lambda$が小さければカーブは直線に近づき、誤差が少なくなります。
なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。
$\dagger$2nd SMのDCである$K_\text{MPF}$を条件付き確率と変更する方式

Leave a Comment