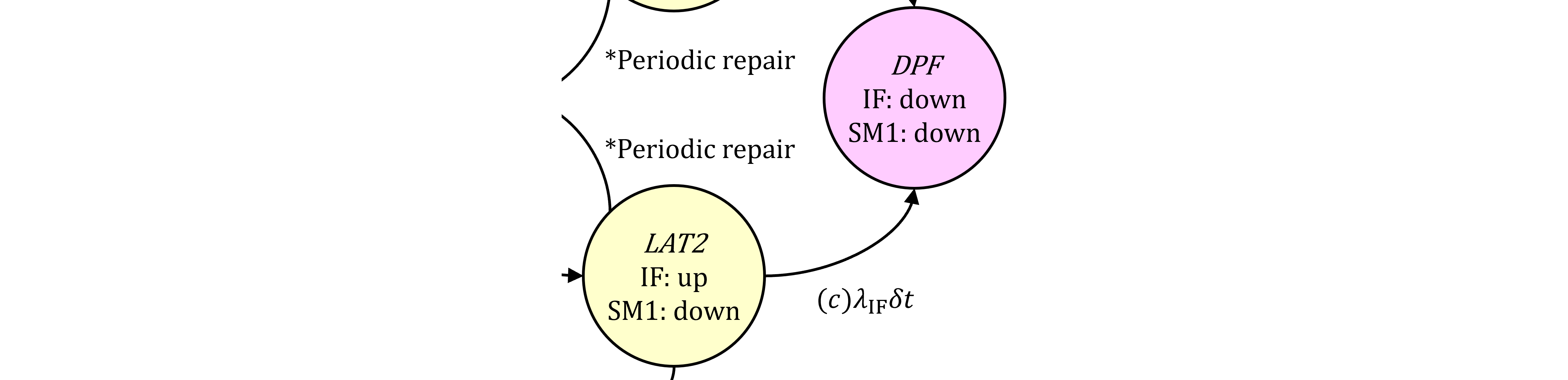
LAT1⇒DPFの平均PUDの計算

最後にLAT1からDPFへの平均PUDを計算します。

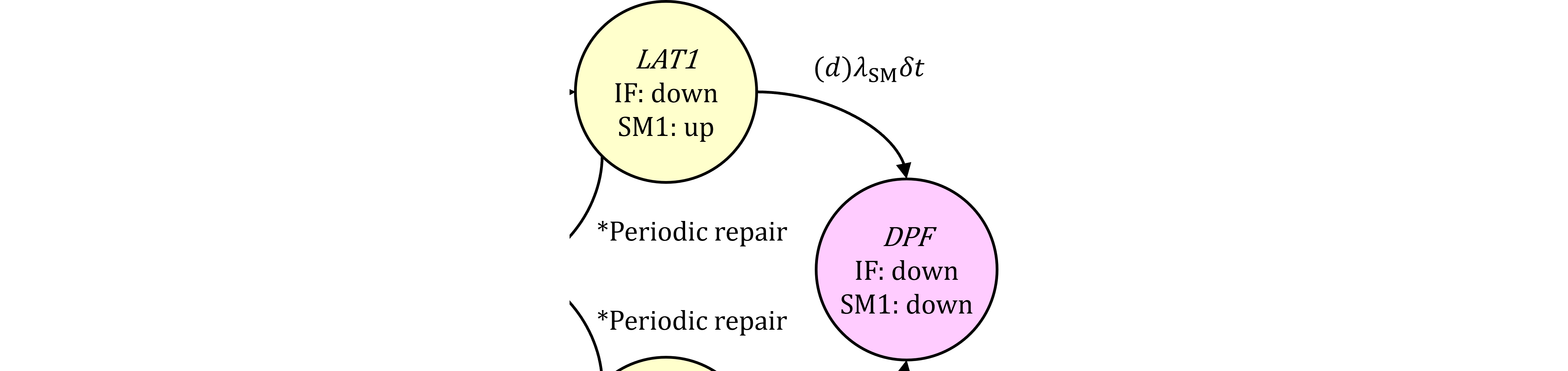
LAT1からDPFへの遷移(d)の平均PUDは、 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF(d),IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF\ via\ (d)\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT1\ at\ }t\cap\mathrm{SM\ down\ in\ }(t, t+dt)\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT1\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT1\ at\ }t\} \end{eqnarray} \tag{372.1} $$ 同様に表368.1より、IF preventableのdown状態は(5)及び(7)であることから、 $$ \Pr\{\mathrm{IF^R_\text{prev}\ down\ at\ }t\}\\ =K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\left[(1-K_\text{IF,MPF})F_\text{IF}(t)+K_\text{IF,MPF}F_\text{IF}(u)\right]\\ =K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}Q_\text{IF}(t) \tag{372.2} $$ となります。よって、 $$ \Pr\{\mathrm{LAT1\ at\ }t\}=\Pr\{\mathrm{IF^R_{prev}\ down\ at\ }t\cap\text{SM up at }t\}\\ =K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\left[(1-K_\text{IF,MPF})F_\text{IF}(t)+K_\text{IF,MPF}F_\text{IF}(u)\right]A_{\mathrm{SM}}(t)\\ =K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}Q_\text{IF}(t)A_{\mathrm{SM}}(t) \tag{372.3} $$ と書けます。

一方、 $$ \require{cancel} \Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT1\ at\ }t\}\\ =\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{SM\ up\ at\ }t\cap\bcancel{\mathrm{IF^R_{prev}\ down\ at\ }t}\}\\ =\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{SM\ up\ at\ }t\}=\lambda_{\mathrm{SM}}dt\tag{372.4} $$ であるから、(372.1)は、(106.4)を用いて、 $$ \begin{eqnarray} (372.1)&=&\frac{K_{\mathrm{IF,RF}}\color{red}{(1-K_\text{IF,det})}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_{\mathrm{IF,MPF}})F_{\mathrm{IF}}(t)+K_{\mathrm{IF,MPF}}F_{\mathrm{IF}}(u)\right]\\ & &\cdot\left[(1-K_\text{SM,MPF})f_\text{SM}(t)+K_\text{SM,MPF}f_\text{SM}(u)\right]dt\\ &\approx&\frac{K_{\mathrm{IF,RF}}\color{red}{(1-K_\text{IF,det})}}{2}\lambda_{\mathrm{SM}}\lambda_{\mathrm{IF}}\left[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau\right]\\ &=&K_{\mathrm{IF,RF}}\color{red}{(1-K_\text{IF,det})}\beta, \end{eqnarray}\tag{372.5} $$

$$ ただし、\begin{cases} \begin{eqnarray} u&:=&t\bmod\tau,\\ \beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau],\\ K_{\mathrm{MPF}}&:=&K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}}\\ \end{eqnarray}\end{cases} $$

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ

LAT2⇒DPFの平均PUDの計算

LAT2⇒DPFの遷移(c)の平均PUDを計算します。

LAT2の状態のうち、(VSG of)IF preventable部分について考えます。 $$ \begin{eqnarray} \overline{q_\mathrm{DPF(c),IFR}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF\ via\ (c)\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2_\text{prev}\ at\ }t\cap\mathrm{IF^R\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^R\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2_\text{prev}\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2_\text{prev}\ at\ }t\} \end{eqnarray} \tag{371.1} $$ 同様に、表368.1よりIF preventableのup状態は従来 (4),(6)及び(8)でしたが、新たに(3)がfaultlessとして加わる ことにより、 $$ \Pr\{\mathrm{IF^R_\text{prev}\ up\ at\ }t\}\\ =K_\text{IF,RF}\color{red}{K_\text{IF,det}}\left[R_\text{IF}(t)+F_\text{IF}(t)\right]+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\left[(1-K_\text{IF,MPF})R_\text{IF}(t)+K_\text{IF,MPF}R_\text{IF}(u)\right]\\ =K_\text{IF,RF}\color{red}{K_\text{IF,det}}+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}A_\text{IF}(t) \tag{371.2} $$ となります。よって、SM1のdownも含めれば、 $$ \Pr\{\mathrm{LAT2_\text{prev}\ at\ }t\}=\Pr\{\mathrm{IF^R_\text{prev}\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\}\\ =\left[K_\text{IF,RF}\color{red}{K_\text{IF,det}}+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}A_\text{IF}(t)\right]Q_\text{SM}(t)\tag{371.3} $$ となります。

一方、(107.7)より、 $$ \require{cancel} \Pr\{\mathrm{IF^R\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ =\Pr\{\mathrm{IF^R\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^R_\text{prev}\ up\ at\ }t\cap\bcancel{\text{SM down at }t}\}\\ =\Pr\{\mathrm{IF^R\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^R\ up\ at\ }t\}=\lambda_\mathrm{IF}dt\tag{371.4} $$ (371.3)、(371.4)を(371.1)に用いれば、 $$ \begin{eqnarray} (371.1)&=&\frac{K_\mathrm{IF,RF}\color{red}{K_\text{det}}\lambda_\text{IF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_\mathrm{SM,MPF})F_\mathrm{SM}(t)+K_\mathrm{SM,MPF}F_\mathrm{SM}(u)]dt,\\ & &+\frac{K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_\mathrm{SM,MPF})F_\mathrm{SM}(t)+K_\mathrm{SM,MPF}F_\mathrm{SM}(u)]\\ & &\cdot\left[(1-K_\mathrm{IF,MPF})f_\mathrm{IF}(t)+K_\mathrm{IF,MPF}f_\mathrm{IF}(u)\right]dt\\ & &ただし、u:=t\bmod\tau\\ \end{eqnarray}\tag{371.5} $$ よって、積分公式(5)及び(107.8)より $$ \begin{eqnarray} (371.5)&\approx& K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha+K_{\text{IF,RF}}\color{red}{(1-K_\text{IF,det})}\beta,\\ ただし、& &\alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau],\\ & &\beta:=\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{MPF})T_\text{lifetime}+K_\mathrm{MPF}\tau],\\ & &K_\mathrm{MPF}:=K_\mathrm{IF,MPF}+K_\mathrm{SM,MPF}-K_\mathrm{IF,MPF}K_\mathrm{SM,MPF} \end{eqnarray} \tag{371.6} $$

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ

LAT2⇒SPFの平均PUDの計算

次にLAT2からSPFの遷移(b)の平均PUDを計算します。この確率積分も、non preventable部分であるため、MPF detectedの変更の影響を受けません。

LAT2の状態のうち、(VSG of)IF non preventable部分について考えます。 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF(b),IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF\ via\ (b)\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2_\overline{prev}\ at\ }t\cap\mathrm{IF^U\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2_\overline{prev}\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2_\overline{prev}\ at\ }t\} \end{eqnarray} \tag{370.1} $$ ここで、表368.1より、IFについてはIF non preventableのupは(2)であるため(369.2)を用い、SMのdownについては(9)+(11)は $$ Q_\text{SM}(t):=(1-K_\text{SM,MPF})F_\text{SM}(t)+K_\text{SM,MPF}F_\text{SM}(u), \\ s.t.\ \ u:=t\bmod\tau $$ を用いれば、 $$ \Pr\{\mathrm{LAT2_\overline{prev}\ at\ }t\}=\Pr\{\mathrm{IF^U_\overline{prev}\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\}\\ =(1-K_\text{IF,RF})R_{\mathrm{IF}}(t)Q_{\mathrm{SM}}(t)\tag{370.2} $$ 一方、(103.4)より、 $$ \require{cancel} \Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2_\overline{prev}\ at\ }t\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U_\overline{prev}\ up\ at\ }t\cap\bcancel{\text{SM down at}t}\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}\\ =\lambda_{\mathrm{IF}}dt\tag{370.3} $$ よって、(370.1)式は、 $$ \begin{eqnarray} (370.1)&=&\frac{1-K_{\text{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt\\ &=&\frac{1-K_{\text{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\text{SM}(t)f_\mathrm{IF}(t)dt\\ \end{eqnarray} \tag{370.4} $$ これに(104.5)の結果を利用すれば、 $$ (370.4)\approx\frac{1-K_{\text{IF,RF}}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}\left[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau\right]\\ \approx(1-K_{\text{IF,RF}})\alpha,\\ ただし、\alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\tag{370.5} $$

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ