|
9 |
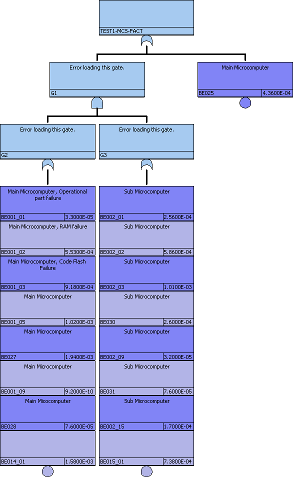
FTAのtree logic (5) |
図903.1のTreeをFault Tree Logic構文で記述したものが以下の表です。
| Fault Tree | Gate | Type | Inputs |
|---|---|---|---|
| ESL | *ESL | OR | GT1, EV2 |
| GT1 | AND | C1, C2, C3 | |
| C1 | OR | TRUE | |
| C2 | OR | GT12, EV166 | |
| GT12 | OR | GT131, GT122, GT130 | |
| GT131 | OR | GT31, GT32 | |
| GT31 | AND | C16, GT35, GT132 | |
| C16 | OR | BE001_23, BE012 | |
| BE001_23 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| GT121 | OR | BE001_09, BE028 | |
| GT1201 | OR | BE027, BE025 | |
| GT35 | OR | BE001_20, GT93 | |
| BE001_20 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| GT93 | OR | C21, GT94 | |
| C21 | OR | EV162, BE008 | |
| EV162 | OR | FALSE | |
| GT94 | OR | GT95, BE001_16 | |
| GT95 | OR | GT97, BE011G, BE010_02 | |
| GT97 | OR | BE002_18, BE002_16 | |
| BE002_18 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_05 | |
| GT118 | OR | BE025, BE030 | |
| GT119 | OR | BE002_09, BE031 | |
| BE002_16 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_05 | |
| BE011G | OR | EV164, BE011 | |
| EV164 | OR | FALSE | |
| BE001_16 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| GT132 | OR | GT117, GT123 | |
| GT117 | OR | GT110, GT124, GT125, GT126 | |
| GT110 | AND | EV188, EV72 | |
| EV188 | OR | FALSE | |
| EV72 | OR | FALSE | |
| GT124 | OR | BE005_02, BE005_01 | |
| BE005_02 | OR | FALSE | |
| GT125 | OR | BE001_18_01, BE001_18_02, BE001_18_03 | |
| BE001_18_01 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_11 | |
| BE001_18_02 | OR | FALSE | |
| BE001_18_03 | OR | FALSE | |
| GT126 | OR | BE005_02, BE005_03 | |
| GT123 | OR | BE001_22_01, BE001_22_02, BE001_22_03 | |
| BE001_22_01 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02 | |
| BE001_22_02 | OR | FALSE | |
| BE001_22_03 | OR | FALSE | |
| GT32 | AND | C16, GT37, GT38, GT133 | |
| GT37 | OR | GT101, BE009 | |
| GT101 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| GT38 | OR | BE001_19, GT103, GT104 | |
| BE001_19 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| GT103 | OR | EV182, BE006 | |
| EV182 | OR | FALSE | |
| GT104 | OR | EV183, BE007 | |
| EV183 | OR | FALSE | |
| GT133 | OR | GT127, GT128 | |
| GT127 | OR | BE013_02, BE013_01 | |
| BE013_02 | OR | FALSE | |
| GT128 | OR | BE001_24_01, BE001_24_02, BE001_24_03 | |
| BE001_24_01 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| BE001_24_02 | OR | FALSE | |
| BE001_24_03 | OR | FALSE | |
| GT122 | OR | BE001_25_01, BE001_25_02, BE001_25_03 | |
| BE001_25_01 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_05 | |
| BE001_25_02 | OR | FALSE | |
| BE001_25_03 | OR | FALSE | |
| GT130 | OR | BE014_02, BE014_01 | |
| BE014_02 | OR | FALSE | |
| EV166 | OR | FALSE | |
| C3 | OR | GT19, EV3, EV185 | |
| GT19 | OR | GT107, GT134, GT135 | |
| GT107 | AND | C11, C13, C14 | |
| C11 | OR | GT87, BE023 | |
| GT87 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_05 | |
| C13 | OR | BE002_18_01, GT91 | |
| BE002_18_01 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_05 | |
| GT91 | AND | BE011G, BE189 | |
| C14 | OR | GT111, GT136 | |
| GT111 | AND | GT109, GT113 | |
| GT109 | OR | GT110, GT137, GT138, GT139 | |
| GT137 | OR | BE002_17_01, BE002_17_02, BE002_17_03 | |
| BE002_17_01 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_15 | |
| BE002_17_02 | OR | FALSE | |
| BE002_17_03 | OR | FALSE | |
| GT138 | OR | BE005_02, BE005_01 | |
| GT139 | OR | BE005_02, BE005_03 | |
| GT113 | OR | GT132, BE002_16_01, BE001_16_01, BE010_01 | |
| BE002_16_01 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_15 | |
| BE001_16_01 | OR | GT121, GT1201, BE001_01, BE001_03, BE001_02, BE001_11 | |
| GT136 | OR | BE002_20_01, BE002_20_02, BE002_20_03 | |
| BE002_20_01 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02 | |
| BE002_20_02 | OR | FALSE | |
| BE002_20_03 | OR | FALSE | |
| GT134 | OR | BE015_02, BE015_01 | |
| BE015_02 | OR | FALSE | |
| GT135 | OR | BE002_21_01, BE002_21_02, BE002_21_3 | |
| BE002_21_01 | OR | GT118, GT119, BE002_01, BE002_03, BE002_02, BE002_15 | |
| BE002_21_02 | OR | FALSE | |
| BE002_21_3 | OR | FALSE | |
| EV3 | OR | FALSE | |
| EV185 | OR | FALSE | |
| EV2 | OR | FALSE | |