|
13 |
Pongと強化学習 (72) |
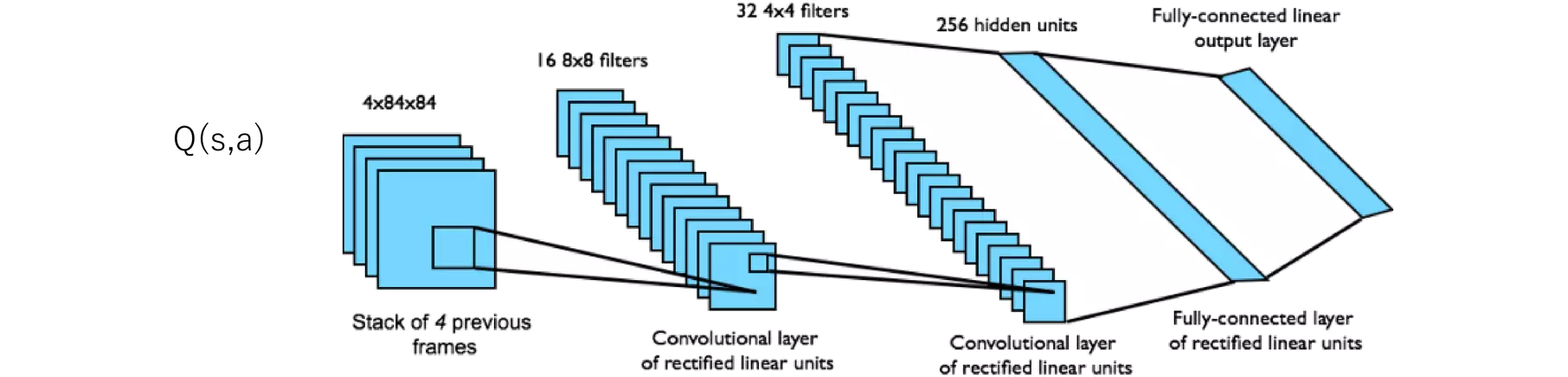
Deep Q-Network (DQN) for Atari GamesというGithubリポジトリがあったので、それに基づいてPongのDQNによるトレーニングをやってみました。
https://github.com/adhiiisetiawan/atari-dqn?tab=readme-ov-file#installation
図893.1は始めたばかりで、緑の学習機のパドルはほとんど打ち返すことができません。ランダムにパドルを動かすだけなので、偶然に打ち返すことはあるものの一点も取れませんでした。

図893.2は約26H経過した後で、緑の学習機のパドル操作は上手になっており、あまりボールを逸らすことはなくなりました。コンピュータ相手に大差で勝てるまで上達しています。

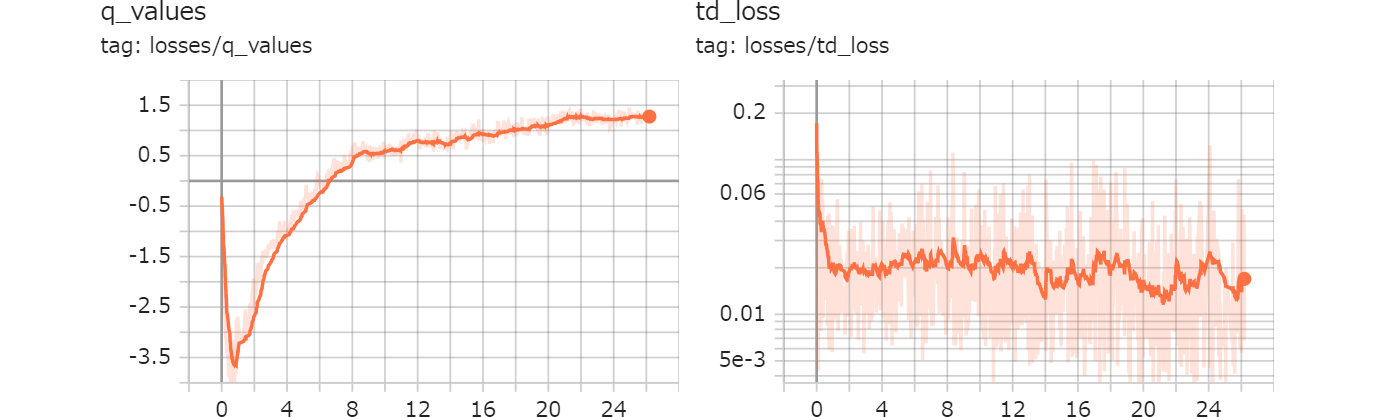
図893.3は約26H経過した後のQ値とTD損失の推移グラフです。横軸の単位は時間です。Q値は報酬と関係しているため、大きいほうが良く、TD損失は誤差であるため、小さいほうが良い行動ということができます。