|
18 |
Pongと強化学習 (64) |
 |
前記事からの続きです。
エージェントという言葉は環境以外の総体を指すようなので聞いててみます。
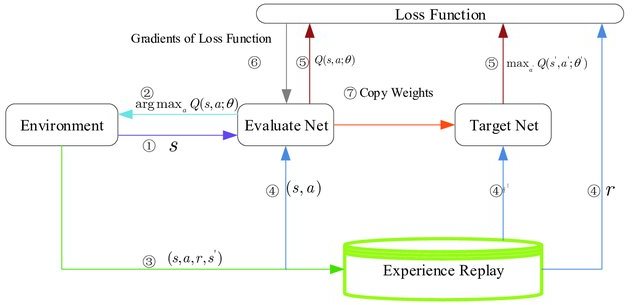
はい、その理解は正しいです。強化学習において、「エージェント」という用語は、学習アルゴリズム、意思決定プロセス、およびその他の学習を支援するメカニズム(Q-network、Target Q-network、Replay Memory、ハイパーパラメータ管理など)を含む総体を指します。環境を除くこれらすべてのコンポーネントが、一般的にエージェントの一部と見なされます。
エージェントの定義
エージェントは、以下を行うシステムまたはエンティティです:
- 環境からの入力(観測)を受け取る:エージェントは環境の現在の状態や、その状態に至るまでの履歴などの情報を受け取ります。
- 行動を選択し、実行する:エージェントは選択した行動を環境に対して実行し、その結果として状態が変化したり報酬を受け取ったりします。
- 学習を行う:エージェントは経験を通じて、より良い行動選択を行うための学習を行います。これには、獲得した報酬を最大化するようなポリシーを見つけるプロセスが含まれます。
- ポリシー(行動選択戦略)を改善する:エージェントは学習プロセスを通じて、ポリシーを継続的に改善し、最終的には目標を達成することを目指します。
環境との区別
エージェントと環境は、強化学習システムの二つの主要な要素です。環境はエージェントが操作し、その操作に対して報酬や新しい状態情報を提供する外部のシステムまたはプロセスです。エージェントと環境は相互作用を通じて互いに影響し合いますが、環境はエージェントによって制御されるわけではなく、そのダイナミクスはエージェントにとって与えられたものとなります。
結論
したがって、「エージェント」という用語は、環境以外の、学習と意思決定に関わるシステム全体を指すのに適切な言葉です。エージェントは、環境との相互作用を通じて、目的を達成するための最適なまたは満足のいく行動戦略を学習する役割を担います。