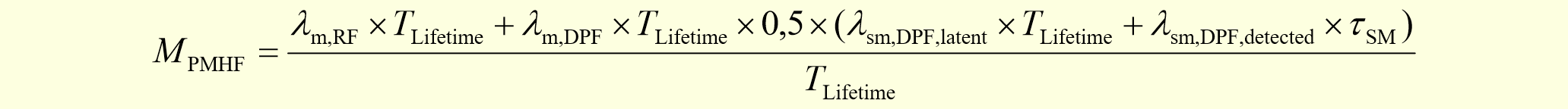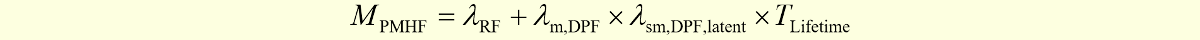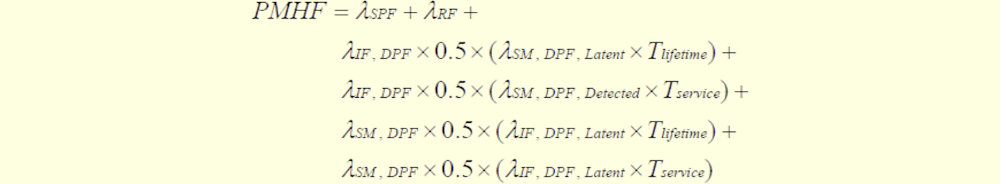|
21 |
ISO 26262のFTAに関する論文 (6) |
 |
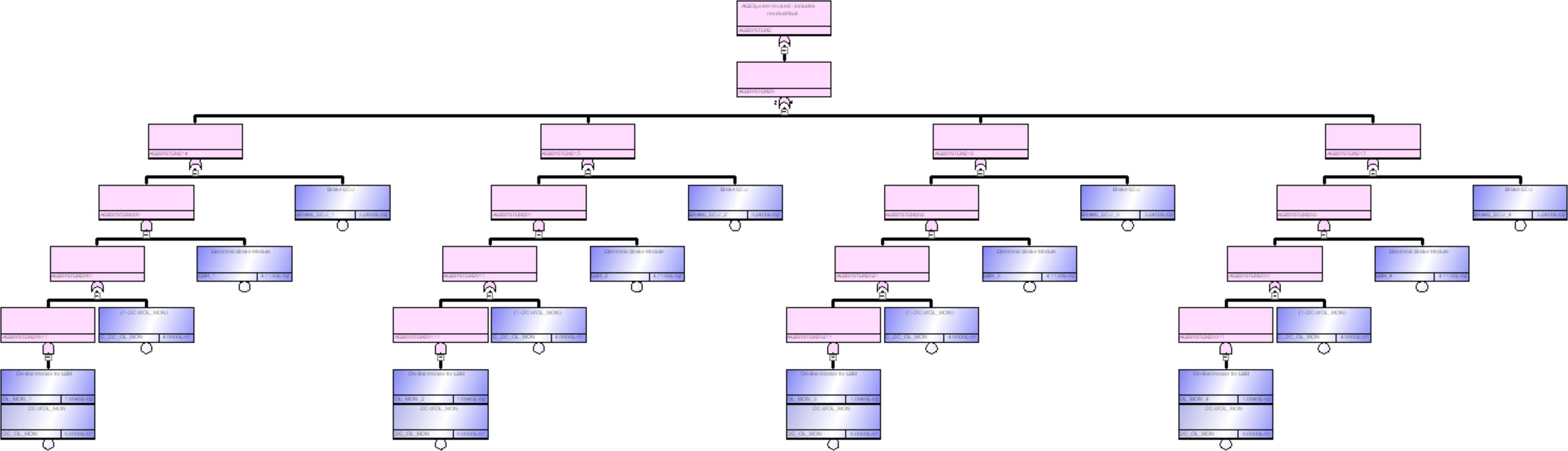
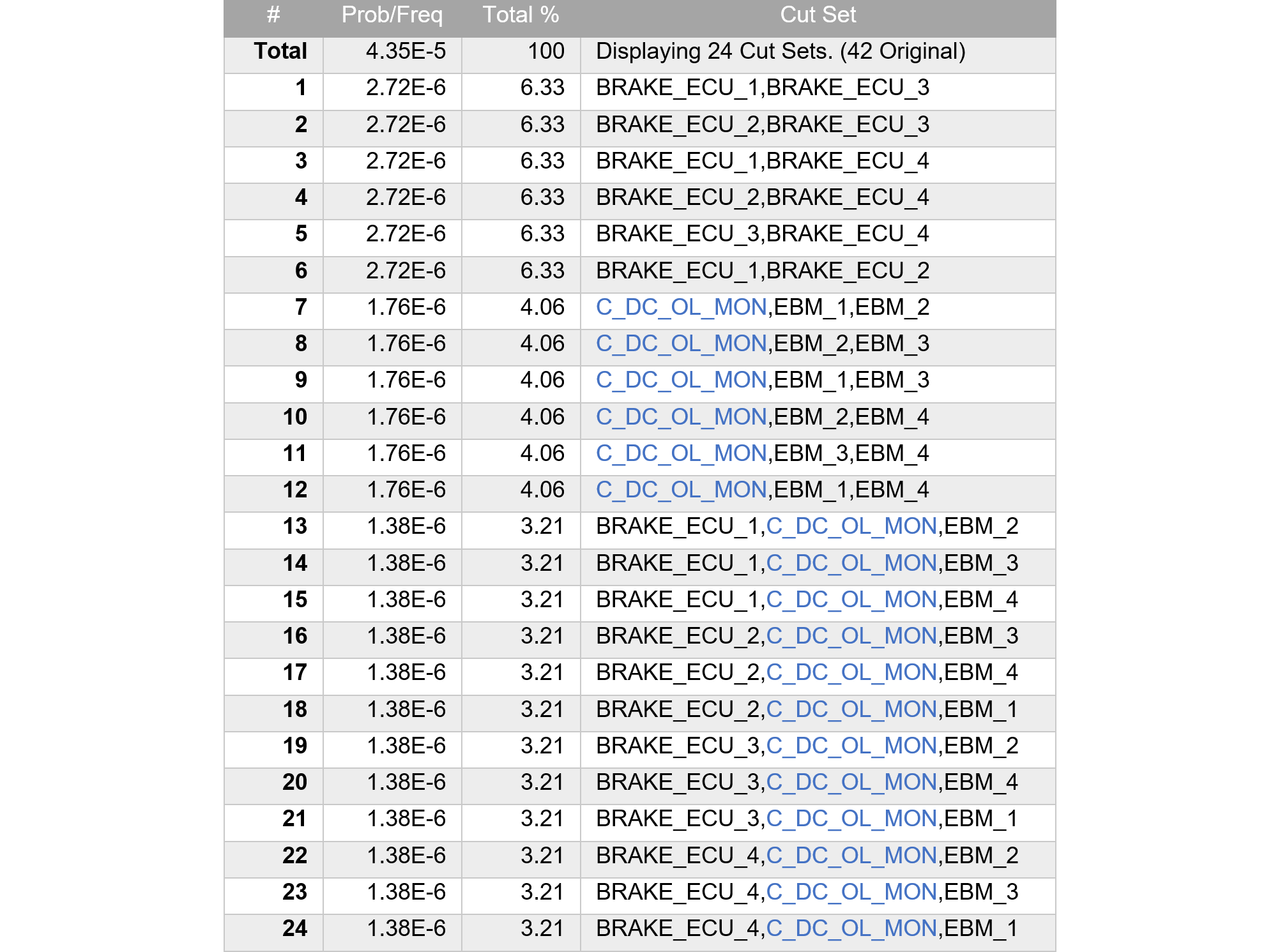
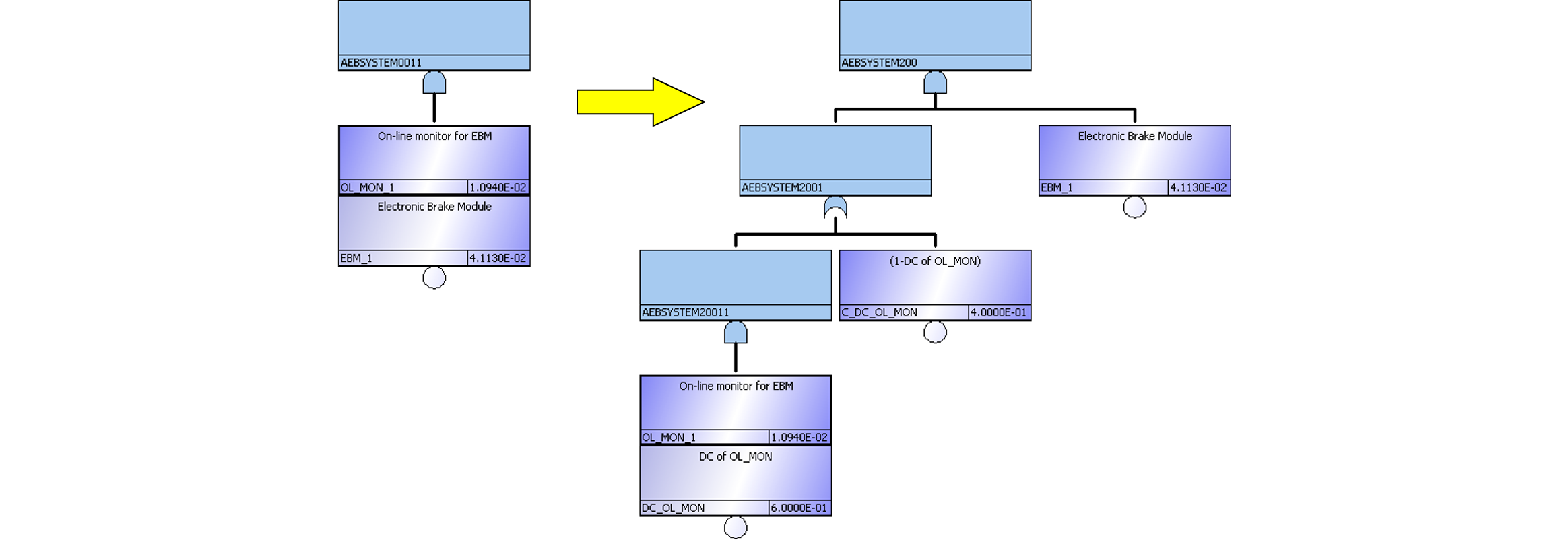
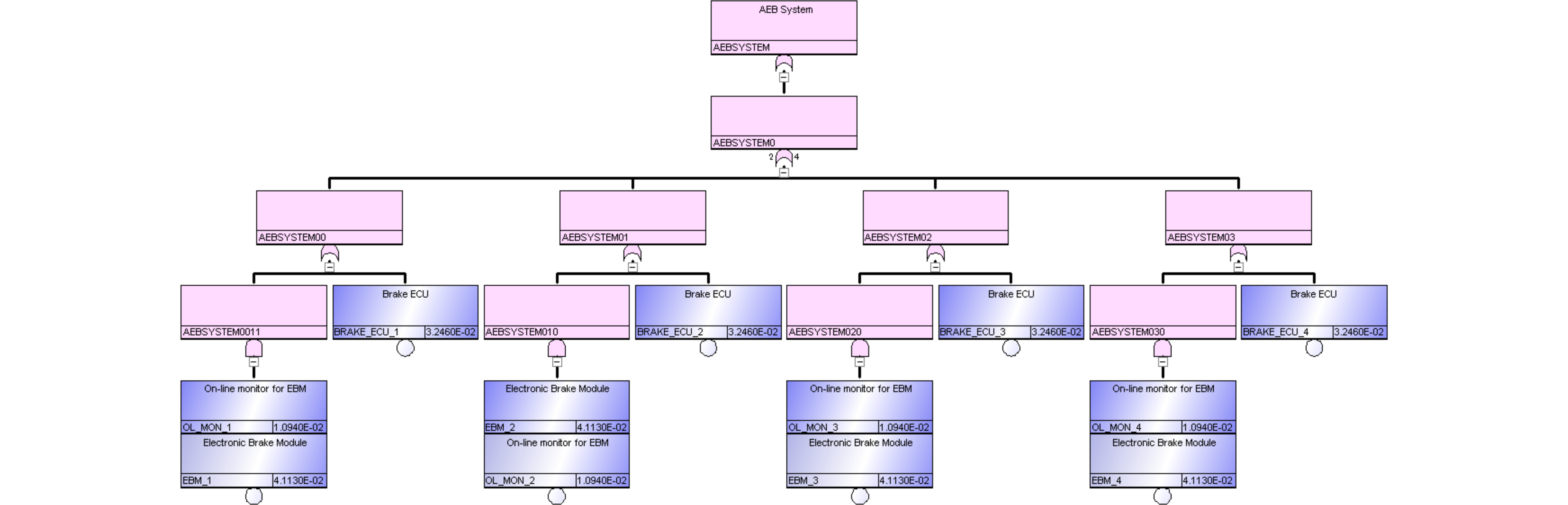
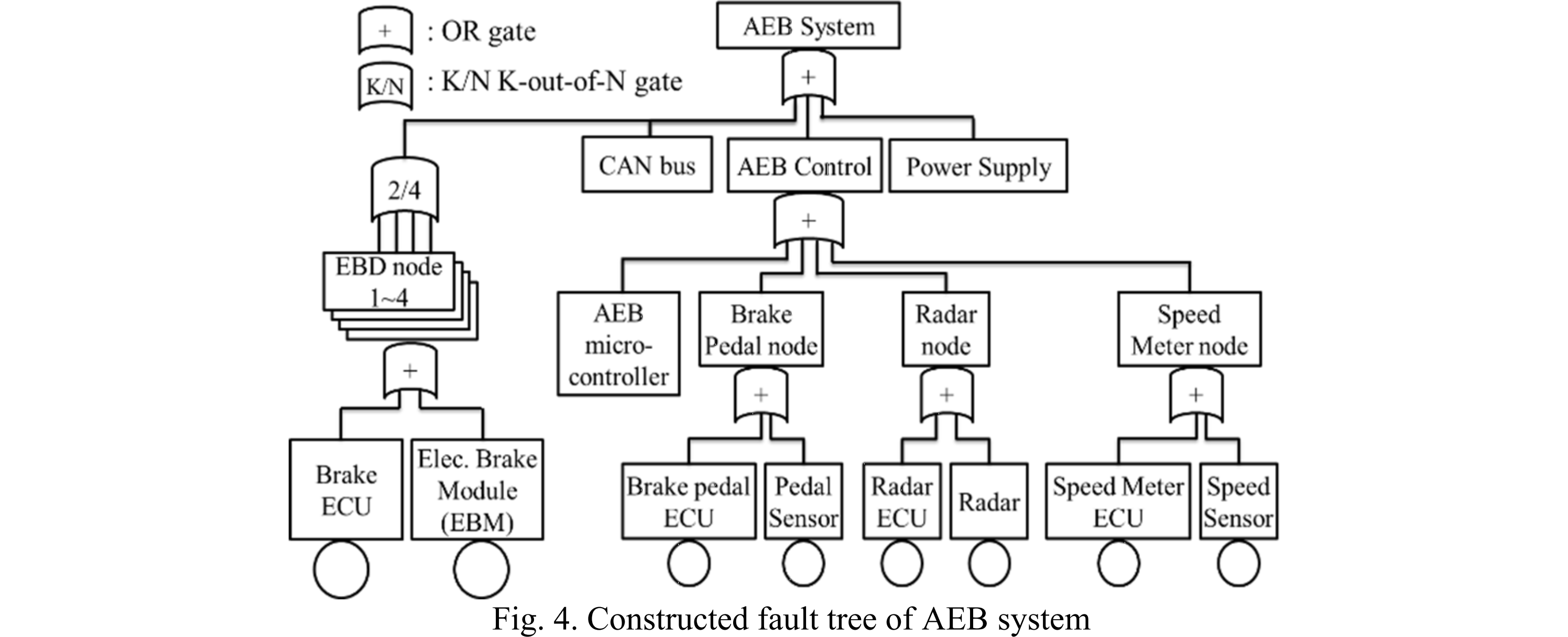
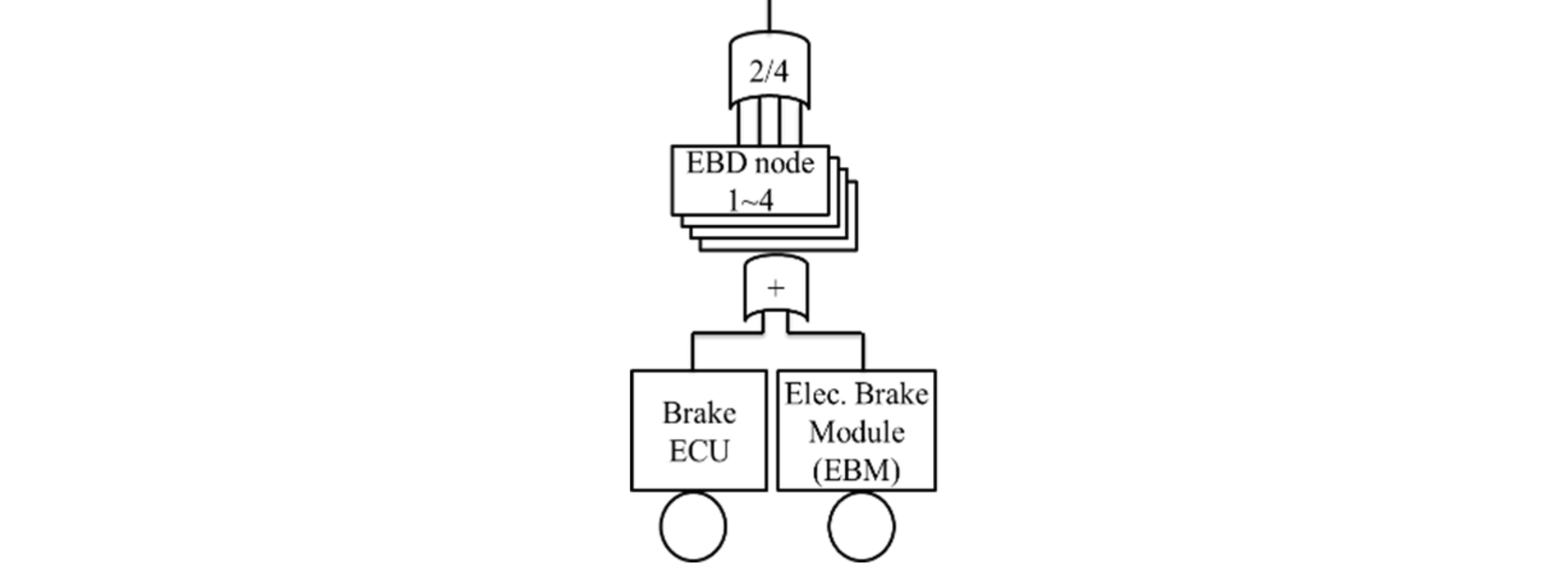
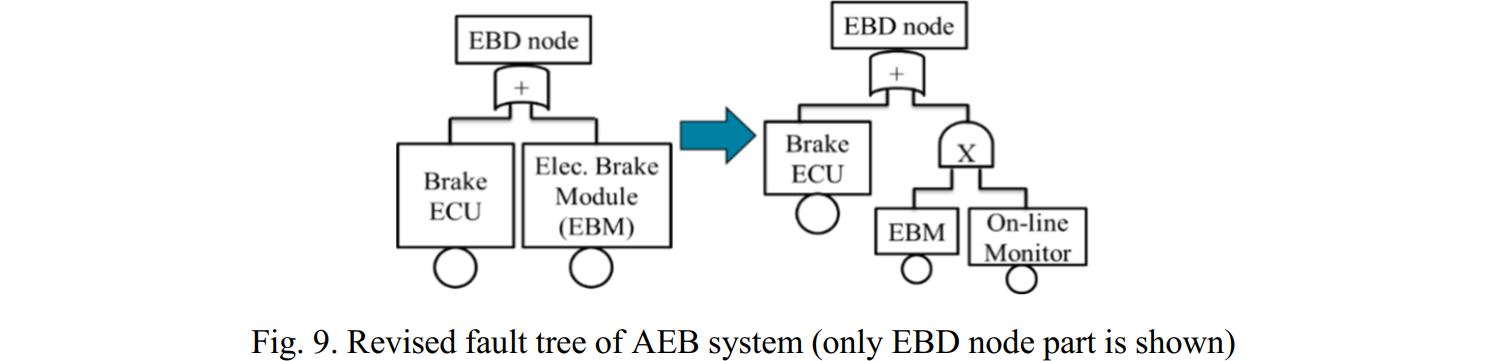
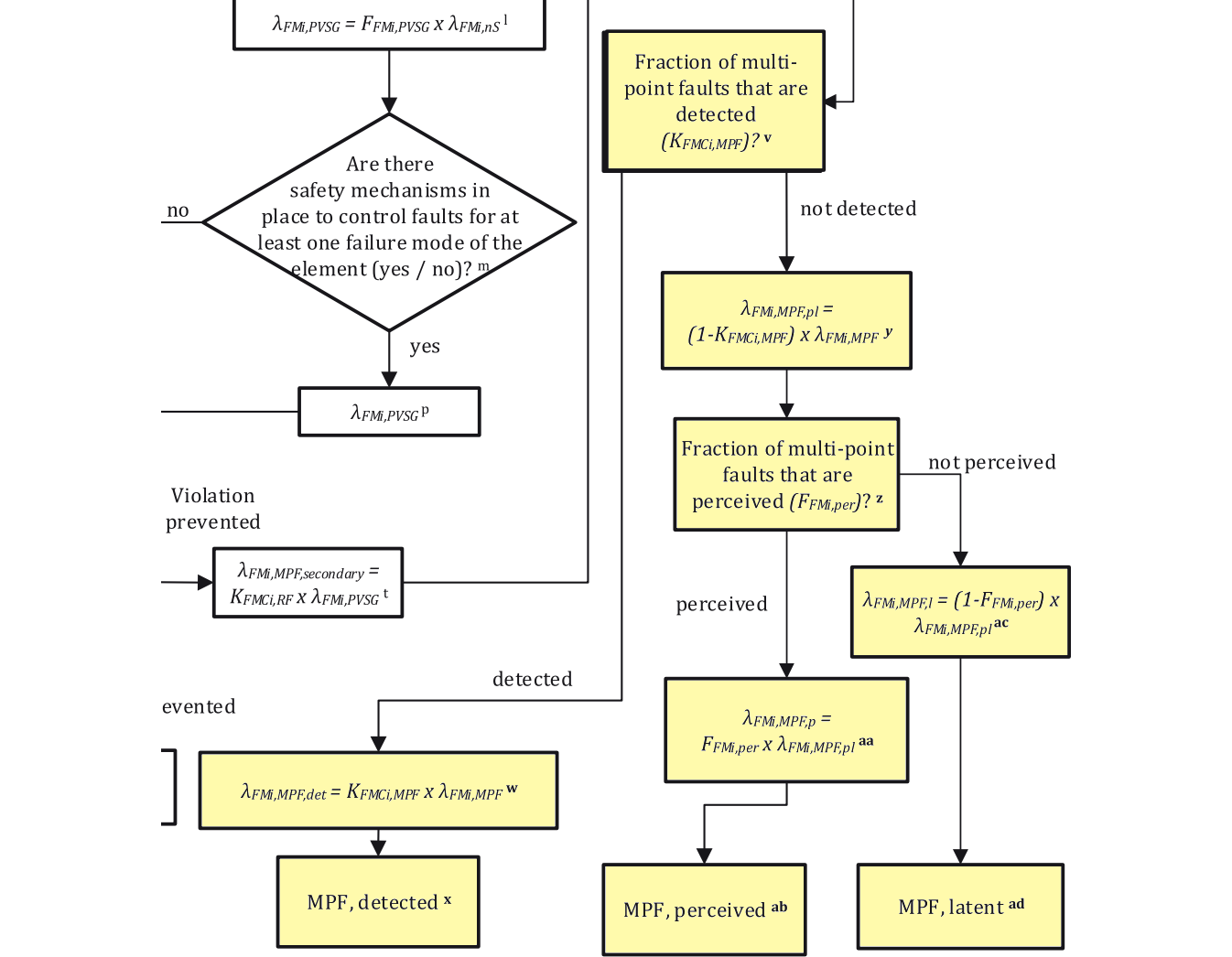
この論文でも、ターゲットの目標値はPMHFとなっていますが、算出において規格のPMHF式を尊重していません。サブシステムの不信頼度を $$F(t)=1-e^{-\lambda t}$$ との式で計算しており、これは修理可能性を考慮していないことを表しています。ただし、前論文とは異なり図206.1の赤で示すように、$\lambda_{RF}=(1-DC)\lambda$は計算に入っているのでましです。ただし、RFと書かれていますが、後で説明するように、これはLFです。1点故障は全て冗長相手チャネルによりVSG抑止されるので、100%レイテントとなるためです。
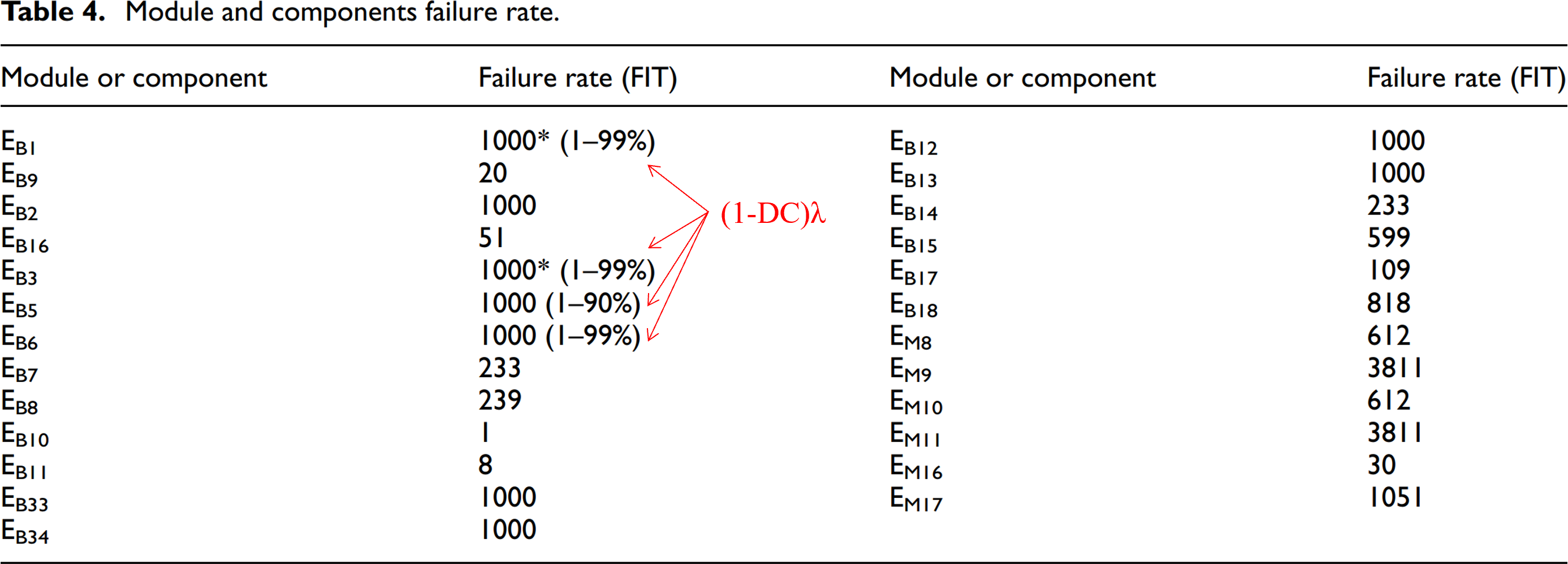
再度整理すると、正しい考え方は、
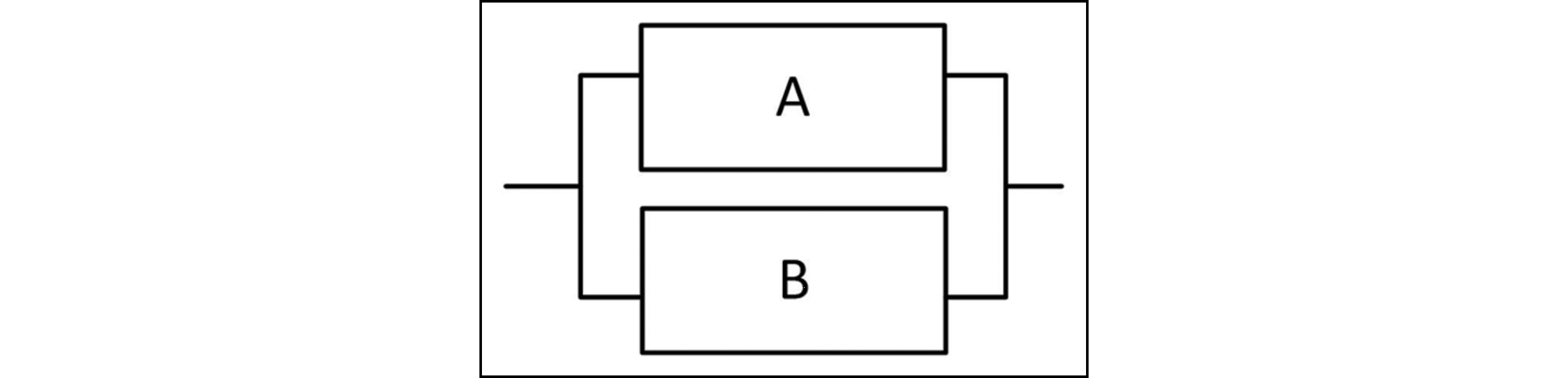
- E1及びE2の2つのエレメントにより構成される冗長系は、マルコフ連鎖で表される。
- E1、E2それぞれのエレメントは修理可能(つまり不信頼度$F(t)$ではなく、不稼働度$Q(t)$となる)
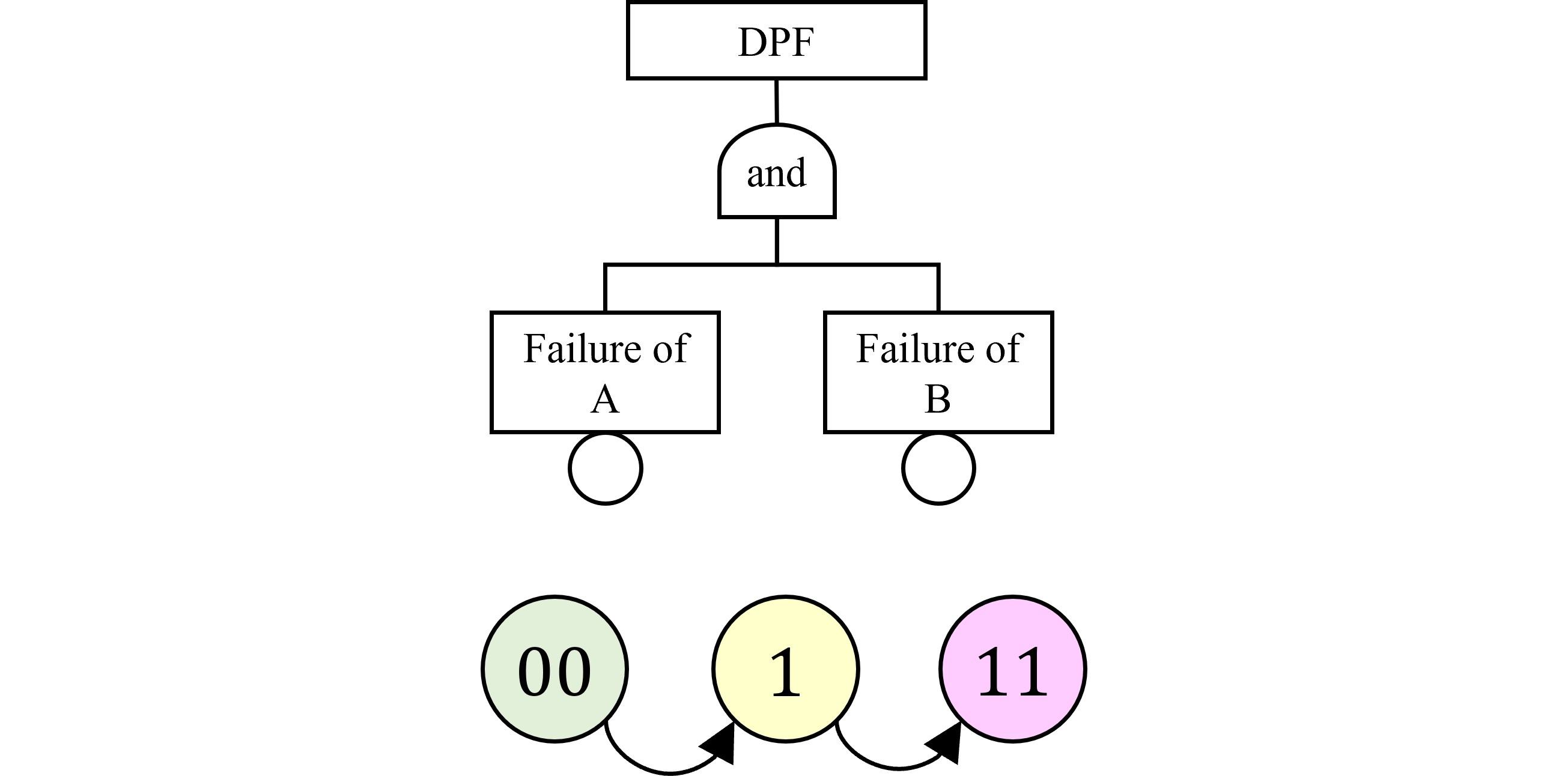
- PMHF式はこれらを考慮し、系の車両寿命における平均不稼働確率Q(T)を表したものであり、 PMHF式に基づきFault Treeを構成する
でなくてはなりませんが、参照論文はこのうち、2.及び3.が満足されていません。
このように専門家であっても同じような誤りを起こす原因は、規格が理解しやすく書かれていないためだと考えます。ただ、規格屋さんに言わせれば、「規格は論文でもなければ教科書でもない」とのことなので、分かりやすさは追究していないようです。そのためこのような解説ブログの存在意義があります。