|
24 |
DPF |
信頼度と故障率の関係式
DPF(Dual Point Failure; 2点故障)を説明する前に、時刻$t$から時刻$t+\Delta t$までの時間にエレメント$A$に関して起こる故障について、図13.1に示します。
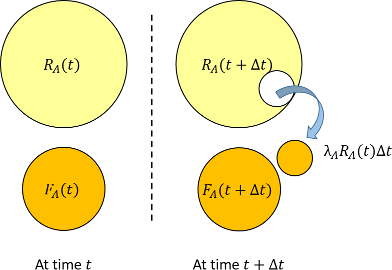
時刻$t$において、故障していない確率が$R_A(t)$であり、時刻$t+\Delta t$までの$\Delta t$時間における信頼度$R_A(t)$の減少分は、(2.6)から$\lambda_A R_A(t) \Delta t=f_A(t)\Delta t$となることから、
\[ R_A(t+\Delta t)=R_A(t)-\lambda_A R_A(t) \Delta t\tag{13.1} \]
DPFを考えるためにエレメント$A$とエレメント$B$の故障を考えます。エレメント$A$,$B$の故障は独立して起こるので、以下のようになります。
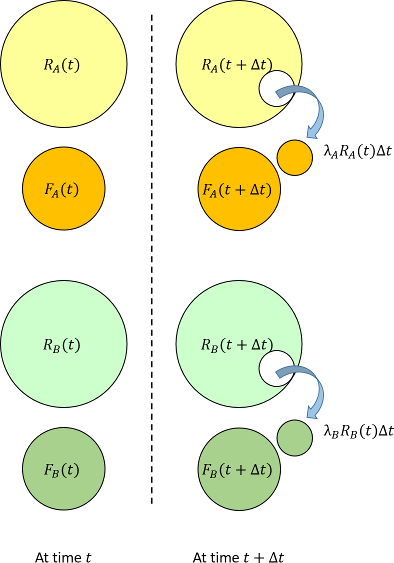
DPF
さて、次にエレメント$A$,$B$が有り、$A$が主機能の場合は$B$はそれに関する安全機構、$A$が安全機構の場合は$B$はそれに関する主機能であるとします。DPFの定義は
「主機能または安全機構が故障してレイテント状態であるときに、それに関する安全機構または主機能の故障が起きること」
であるため、「エレメントAが故障してレイテント状態であるときに、エレメントBの故障が起きること」を$A\Rightarrow B$で表し、「エレメントBが故障してレイテント状態であるときに、エレメントAの故障が起きること」を$B\Rightarrow A$で表すとき、以下の図13.3のように、どちらが先に故障するかによって、$A\Rightarrow B$または$B\Rightarrow A$の2つの場合となります。また、それらは排他であるため確率は和で表されます。


Leave a Comment