測度論に戻り、集合の包含関係を確認します。この記事は応用のための確率論から引用しています。

集合族$\mathfrak{I}$

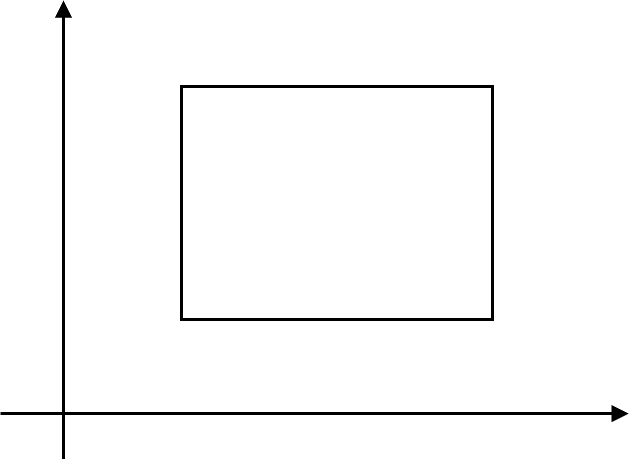
長方形の面積を考えます。平面を集合と考えると、平面に属する点の集合は、$\mathbb{R}^2$で表されます。これを全体の集合$X(=\mathbb{R}^2)$とすると、長方形は$X$上の4点で定義されます。その全ての集合を$\mathfrak{I}$とすると、 $$\mathfrak{I}\subset X$$

集合族$\mathcal{J}$

次に、$\mathfrak{I}$から有限個の長方形を取り出し和を取った図形全体の集合を$\mathcal{J}$とすると、明らかに $$\mathfrak{I}\subset\mathcal{J}\subset X$$

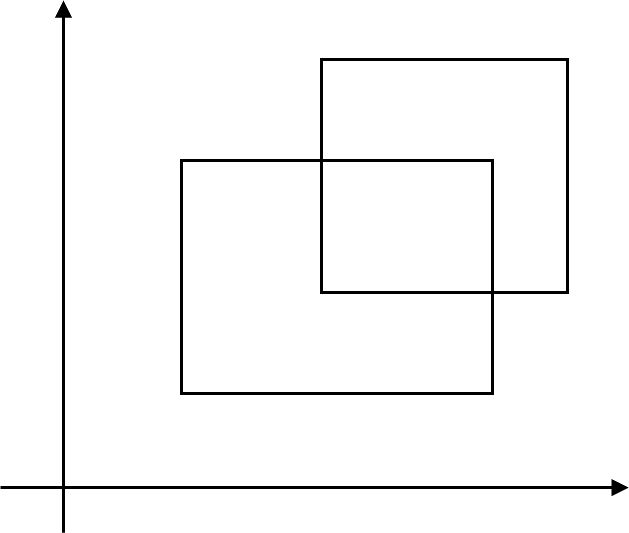
オーバーラップしていますが、互いに背反(ノンオーバーラップ)な長方形を用いて等価変換できます。

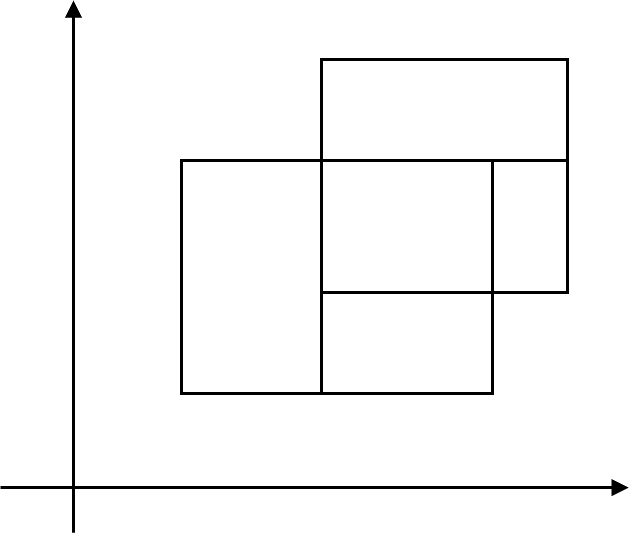
集合族$\mathcal{T}$

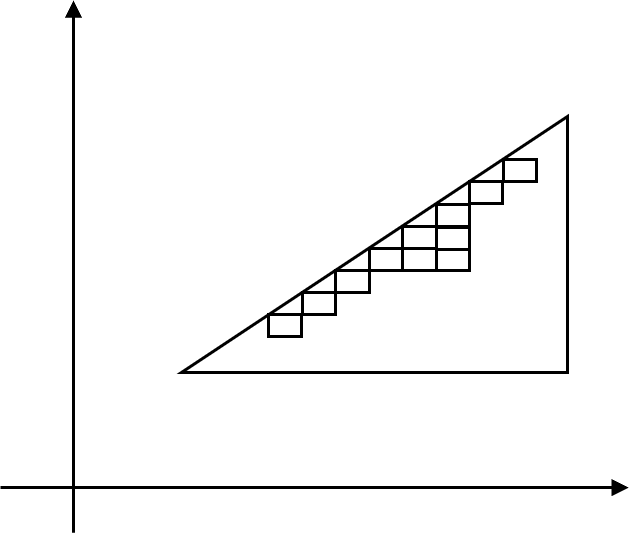
一方、円や三角形等の図形は有限個の長方形では表せないため、高々加算個の背反な長方形$E_i$を用いて、 $$\sum_{i=1}^\infty E_i$$ で表される図形全体の集合を$\mathcal{T}$とすると、 $$\mathfrak{I}\subset\mathcal{J}\subset\mathcal{T}\subset X$$

集合族$\mathfrak{B}_2$

次に$\sigma$代数$\mathcal{F}$を考え、以下の性質を持つものとします。

長方形は全て$\mathcal{F}$に含まれる。

$E\in\mathcal{F}$ならば$E^c=X-E\in\mathcal{F}$

$E_i\in\mathcal{F}\ (i=1,2,...)$ならば$\bigcup_{i=1}^\infty E_i\in\mathcal{F}$

この性質を持つ$\mathcal{F}$は、この性質から $$\mathcal{T}\subset\mathcal{F}$$ となります。この性質を持つ様々な$\mathcal{F}_{\alpha}$の共通部分を

$$\mathfrak{B_2}=\bigcap_\alpha\mathcal{F}_\alpha$$ とし、これをボレル集合族と呼びます。あきらかにこれは$\mathcal{F}$の集合族の中で最小の集合族です。

集合族$\mathfrak{M}_\mu$

ボレル集合族は$\sigma$加法族として加法性が成立しているため、使いやすいものの、ボレル集合族に含まれる集合$A\in\mathfrak{B_2}$に対して測度$\mu(A)=0$となる$A$の部分集合が必ずしも$\mathfrak{B_2}$に含まれないため、これを全て加え拡張した集合族を$\mathfrak{M}_\mu$とします。

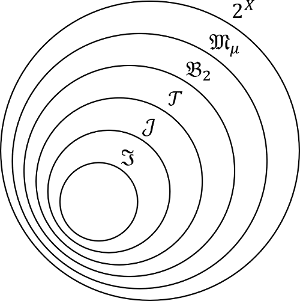
これらの集合族の包含関係を図示すると、図197.1のようになります。

前のブログ 次のブログ