|
23 |
PUAの再検討 |
記事ではChatGPTにグラフを3本書いて貰いました。区間差分をどのように取るかの違いの3種類のグラフです。
- 修理対象=区間内の累積分布=区間不稼働度の差分: $Q_\text{exact}(t)$においては$Q(i\tau)-Q((i-1)\tau)$
- 修理対象=区間内の累積分布=区間不信頼度が一定: $Q_\text{approx1}(t)$においては$-F(\tau)$
- 修理対象=区間内の累積分布=区間不信頼度の差分: $Q_\text{approx2}(t)$においては$F(i\tau)-F((i-1)\tau)$
再考したところ、区間内での不信頼度の増分に対して修理するのはいかにも不自然に思えてきました。SMは区間内で不信頼度の増加を認識せず、区間内での全ての故障に対してK倍で修理を行うためです。 そこで、区間内修理対象(K倍したら修理度になる数値)を以下のように定義します。
- 修理対象=区間不稼働度そのもの: $Q_\text{exact2}(t)$においては$Q(i\tau)$
そしてこのようなPUAのグラフを描いたところ、他のグラフとは様相が異なりました。図の赤がexact2です。
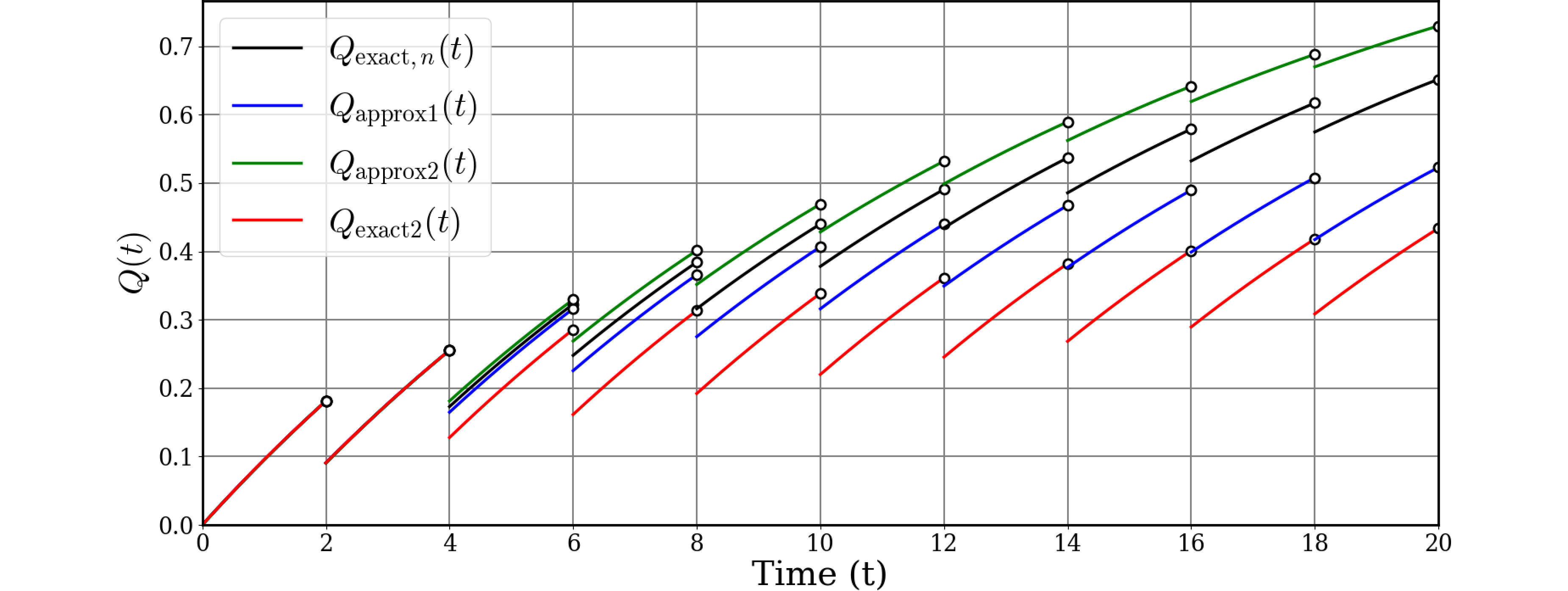
これではバラバラで分かりにくいので、故障率$\lambda$を0.005に下げてみました。
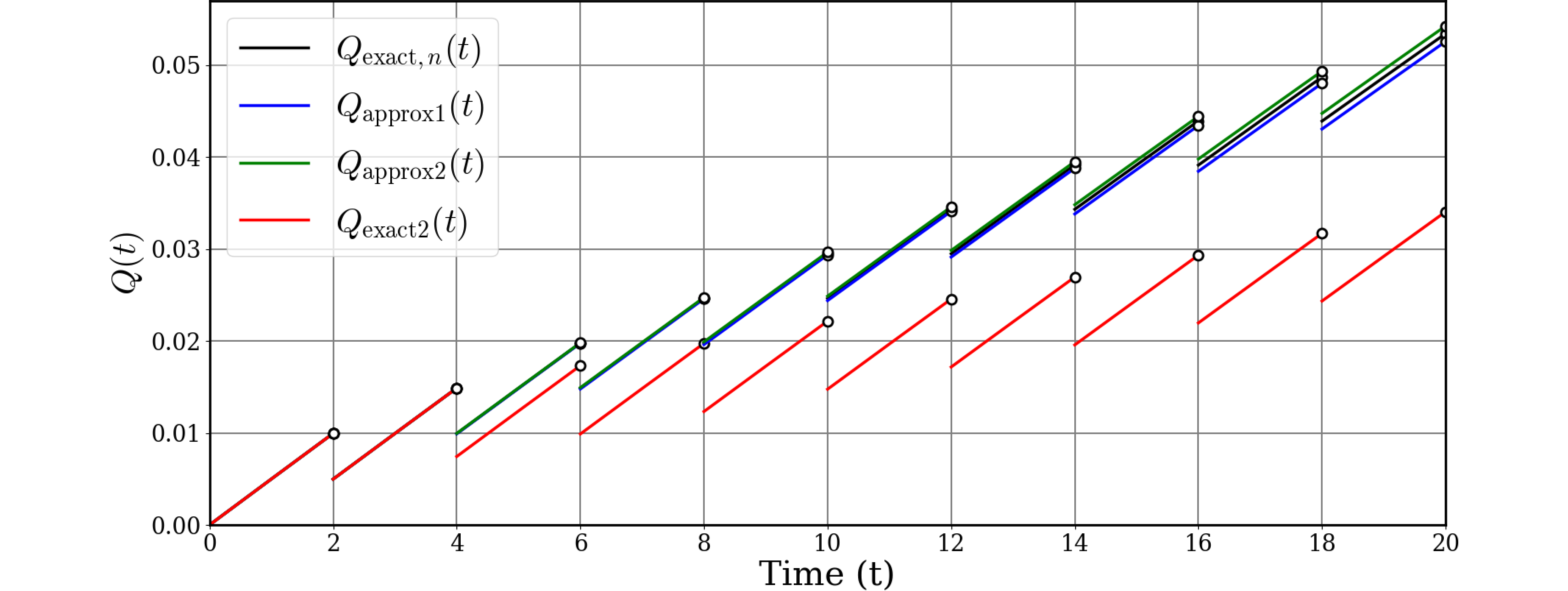
このように、故障率が低い場合は他の3つは収束するのに比べて今回のPUAはかなり低い値を取ります。

Leave a Comment