和文は英文の後に続きます。
(English text comes here.)
信頼度と故障率の関係
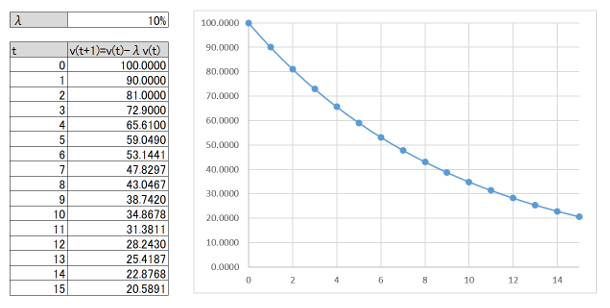
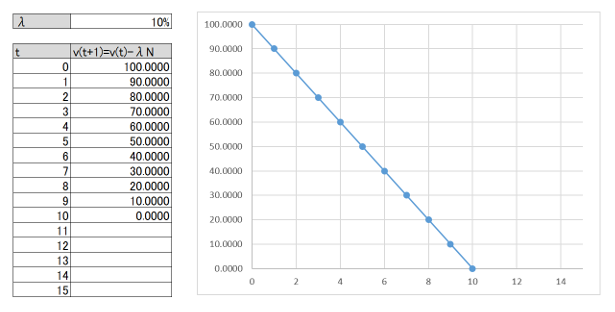
前回は簡単にするために平均故障率は定数としましたが、一般的には故障率は時間の関数であるため、(1.1)は(2.1)と表されます。
\[
v(t+1)-v(t)=-\hat{\lambda}(t)\cdot v(t) \tag{2.1}
\]
さて、「信頼度」はJISにより、「アイテムが、与えられた条件で規定の期間中, 要求された機能を果たす確率」と定義されています。これにより、時刻$t$において、アイテムとしての機能を果たす確率=信頼度$R(t)$は、良品数$v(t)$を$t=0$のときの部品数$v(0)=N$で割ったもので定義され、(2.2)と表されます。
信頼度の定義式:
\[
R(t) \stackrel{def}=\frac{v(t)}{v(0)}=\frac{v(t)}{N} \tag{2.2}
\]
(2.1)の両辺を$N$で割ると(2.3)となります。
\[
\frac{v(t+1)}{N}-\frac{v(t)}{N}=-\hat{\lambda}(t)\cdot \frac{v(t)}{N} \tag{2.3}
\]
この(2.3)に、信頼度$R(t)$の(2.2)を適用すれば、(2.4)が求められます。
\[
R(t+1)-R(t)=-\hat{\lambda}(t)\cdot R(t) \tag{2.4}
\]
さて、ここで1から信頼度$R(t)$を引いた値は不信頼度$F(t)$と呼ばれ、時刻$t$においてアイテムが故障している確率を意味します。
不信頼度の定義式:
\[
F(t) \stackrel{def}{=} 1-R(t) \tag{2.5}
\]
「信頼性」は一般的に良く知られている言葉ですが、信頼度や不信頼度は耳慣れない用語かもしれません。しかし、不信頼度はアイテムが故障している状態を表す大変重要な用語ですので、ぜひ慣れて頂きたいと思います。不信頼度は累積故障確率、故障関数、累積分布関数(Cumulative Distribution Function, CDF)等、いろいろな名前で呼ばれることがあります。
信頼度と不信頼度の導出
(2.4)から平均故障率と信頼度との関係が見えてきました。ここで、一時間後ではなく、$\Delta t$時間後を考えます。この$\Delta t$は微小時間間隔を意味します。これにより、時間間隔$[t, t+\Delta t)$において(2.4)左辺は(2.6)となります。
\[
\frac{1}{\Delta t}\cdot[R(t+\Delta t)-R(t)]=-\hat{\lambda}(t)\cdot R(t) \tag{2.6}
\]
(2.6)において$\Delta t \rightarrow 0$という極限をとれば、平均故障率$\hat{\lambda}(t)$は瞬間故障率$\lambda(t)$となり、(2.7)となります。
\[
\lim_{\Delta t \to 0} \frac{1}{\Delta t}\cdot[R(t+\Delta t)-R(t)]=\frac{dR(t)}{dt}=-\lambda(t)\cdot R(t) \tag{2.7}
\]
(2.7)は$R(t)$に関する微分方程式です。これは信頼度と故障率の関係を示しているため、移項して故障率の式に変形すれば、(2.8)となります。
\[
-\lambda(t)=\frac{1}{R(t)} \frac{dR(t)}{dt}=\frac{d}{dt}\ln R(t) \tag{2.8}
\]
よって、(2.8)の両辺を$t$で積分すれば、(2.9)が求められます。
$$
-\int\lambda(t)dt=\ln R(t)+C \tag{2.9}
$$
さらにこれを指数の形に変形すれば、$R(t)$に関する(2.10)となります。
\[
R(t)=e^{-\int\lambda(t)dt-C} \tag{2.10}
\]
初期状態$t=0$では故障は無いと仮定していることから、$R(0)=1$です。これを(2.10)に適用すると、積分定数$C$は$C=0$と求められます。これを(2.10)に戻せば、(2.11)が得られます。
信頼度の式:
\[
R(t)=e^{-\int\lambda(t)dt} \tag{2.11}
\]
以上から信頼度$R(t)$を求めることができました。これにより、(2.11)を(2.5)に代入すれば不信頼度$F(t)$が(2.12)のように求められます。
不信頼度の式:
\[
F(t)=1-R(t)=1-e^{-\int\lambda(t)dt} \tag{2.12}
\]
 前のブログ
次のブログ
前のブログ
次のブログ