|
8 |
従来手法のPMHF式のまとめ |
PMHFの導出の前提には2通りあります。具体的には、1st SMによって検出され、VSG抑止されたフォールト(MPF detected fault)に関して、
- MPF detected faultをlatent faultとする
- MPF detected faultを直ちに修理する
の2通りの立場があります。規格にはMPF detected faultの処置について明確に書かれていないので、従来はLFとするとしていました。この前提に基づき2020 RAMS論文を投稿しています。
ところが、これだとLFMの定義と矛盾するので、その矛盾の解消のため、2番目の立場を採用した2022 RAMS論文(IEEE未収録)を投稿しました。
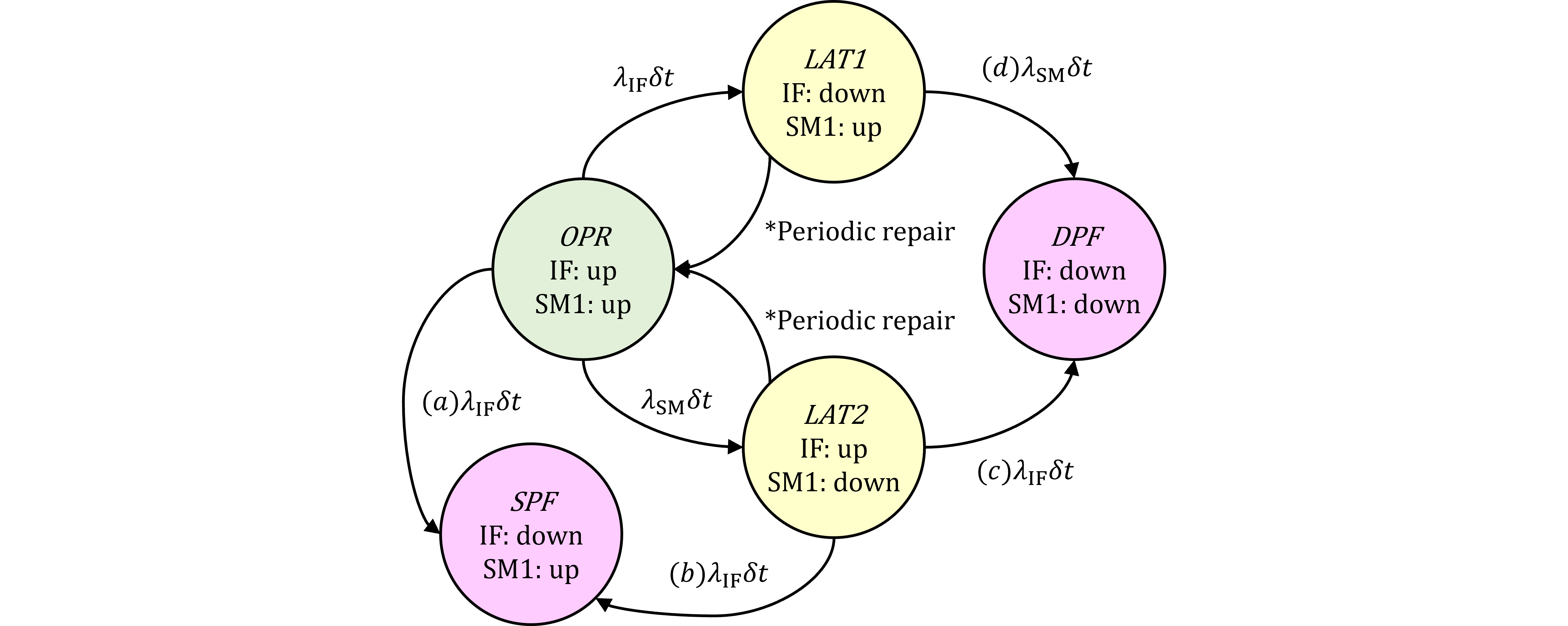
後者のまとめの記事は記事#374に書きましたが、前者をまとめていませんでしたので、以下に表を用いてまとめます。元になる表と導出法は、それぞれ表375.1及び表368.2と記事#376です。
| (a)SPF | (b)SPF | (c)DPF | (d)DPF | |
|---|---|---|---|---|
| LAT2分離 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$(376.1) | $(1-K_\text{IF,RF})\alpha$ (376.2) |
$K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha\\\ +K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta$(376.3) | $K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha\\\ +K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta$(376.4) |
| SPF/DPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $2K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha+2K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta$ | ||
| 規格式1$\dagger\text{SM1}⇒\text{IF}$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha+K_{\mathrm{IF,RF}}\color{red}{(1-K_\text{IF,det})}\beta$ | |||
| 規格式3$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+2K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha+2K_{\mathrm{IF,RF}}\color{red}{(1-K_\text{IF,det})}\beta$ | |||
$$ \text{ただし、} \begin{cases} \alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ \beta:=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \end{cases}\\ \begin{cases} \begin{eqnarray} 非冗長系の時は\color{red}{K_\text{IF,det}}&=&1\\ 冗長系の時は\color{red}{K_\text{IF,det}}&=&0, K_\text{IF,RF}=1\\ \end{eqnarray} \end{cases} $$
表492.1に対して、非冗長系、冗長系のKパラメータを上記に示すとおり代入した表を表492.2及び表492.3に示します。
非冗長系
| (a)SPF | (b)SPF | (c)DPF | (d)DPF | |
|---|---|---|---|---|
| LAT2分離 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$ | $(1-K_\text{IF,RF})\alpha$ | $K_{\text{IF,RF}}\alpha$ | $K_{\text{IF,RF}}\alpha$ |
| SPF/DPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $2K_{\text{IF,RF}}\alpha$ | ||
| 規格式1$\dagger\text{SM1}⇒\text{IF}$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\alpha$ | |||
| 規格式3$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+2K_{\text{IF,RF}}\alpha$ | |||
$$ M_\text{PMHF,NRD}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+2K_{\text{IF,RF}}\alpha}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau] \tag{492.1}$$
(492.1)に関しては後者の記事、#374との違いは係数2の違いとなります。
冗長系
| (a)SPF | (b)SPF | (c)DPF | (d)DPF | |
|---|---|---|---|---|
| LAT2分離 | $0$ | $0$ | $\beta$ | $\beta$ |
| SPF/DPF統合 | $0$ | $2\beta$ | ||
| 規格式1$\dagger$ | $\beta$ | |||
| 規格式3$\dagger$ | $2\beta$ | |||
$$M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}=\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\tag{492.2}$$
(492.2)に関しては後者の記事、#374との違いはありません。その理由は、冗長系においてはMPF detected faultが存在しないためです。
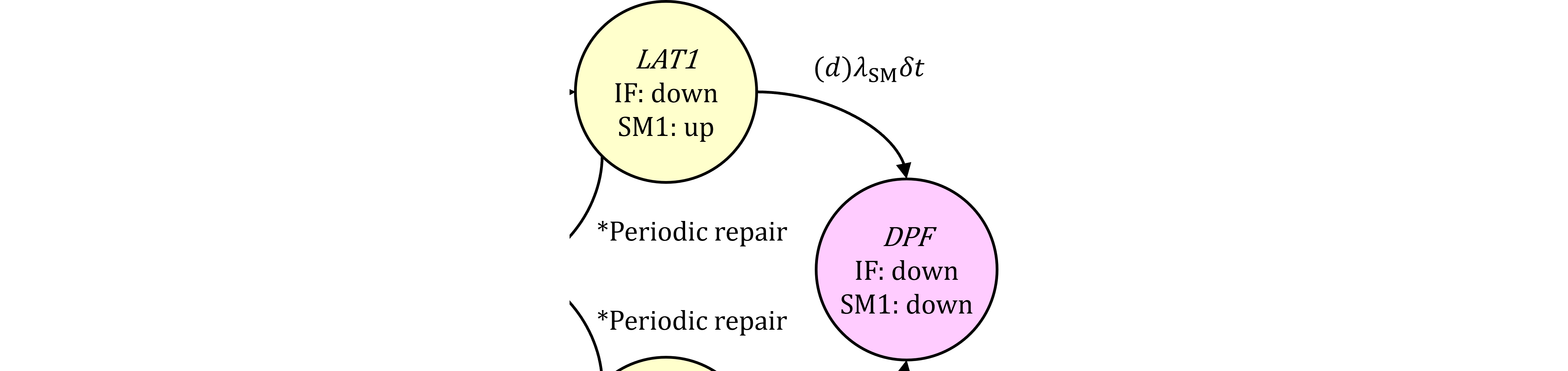
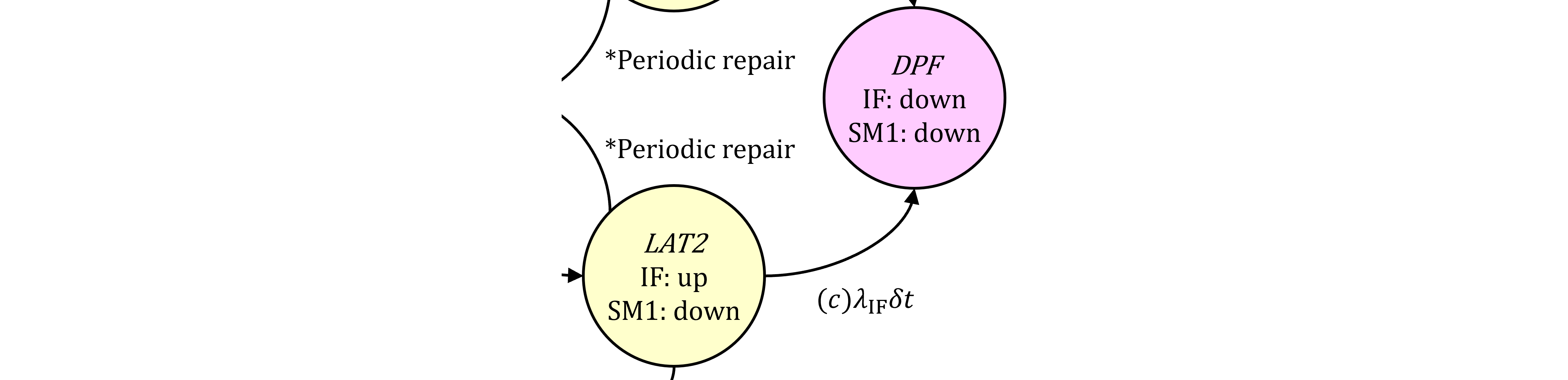
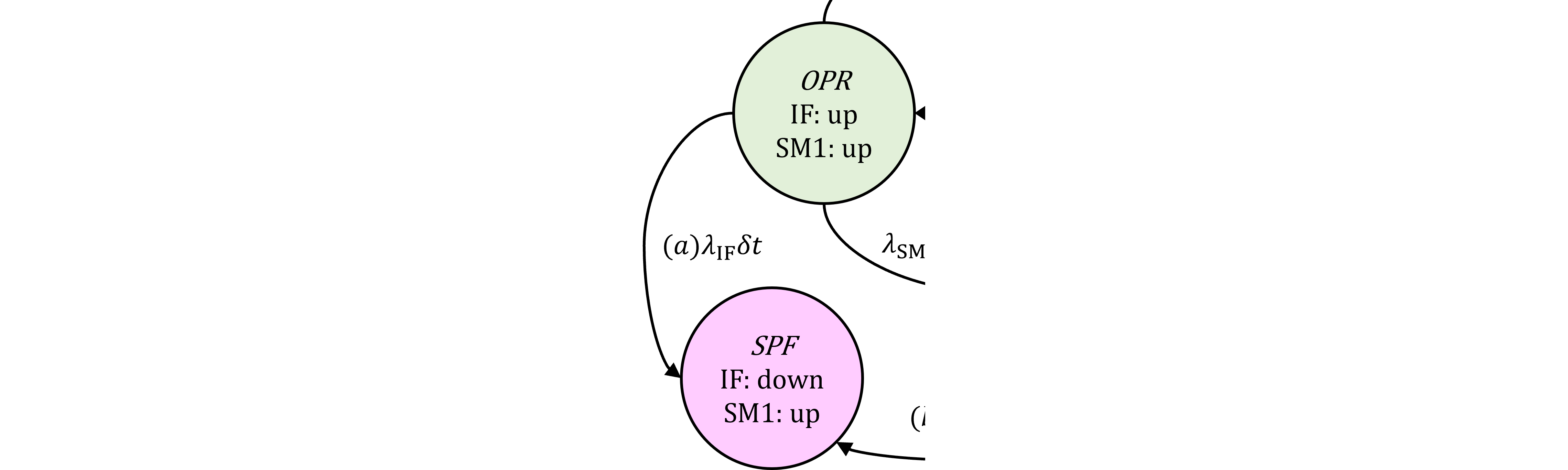
$\dagger$規格式1: 規格第1版 Part 10-8.3.3の第1式の条件。ブログの図367.1)において、IFが後にフォールトする場合=(a)SPF、(b)SPF及び(c)DPF。(d)DPFはSMが後にフォールトする場合なので対象外
$\dagger$規格式3: 規格第1版 Part 10-8.3.3の第3式の条件。ブログの図367.1)において、IF, SMのフォールトの順を問わない場合=(a)SPF、(b)SPF、(c)DPF及び(d)DPF。
RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。