|
31 |
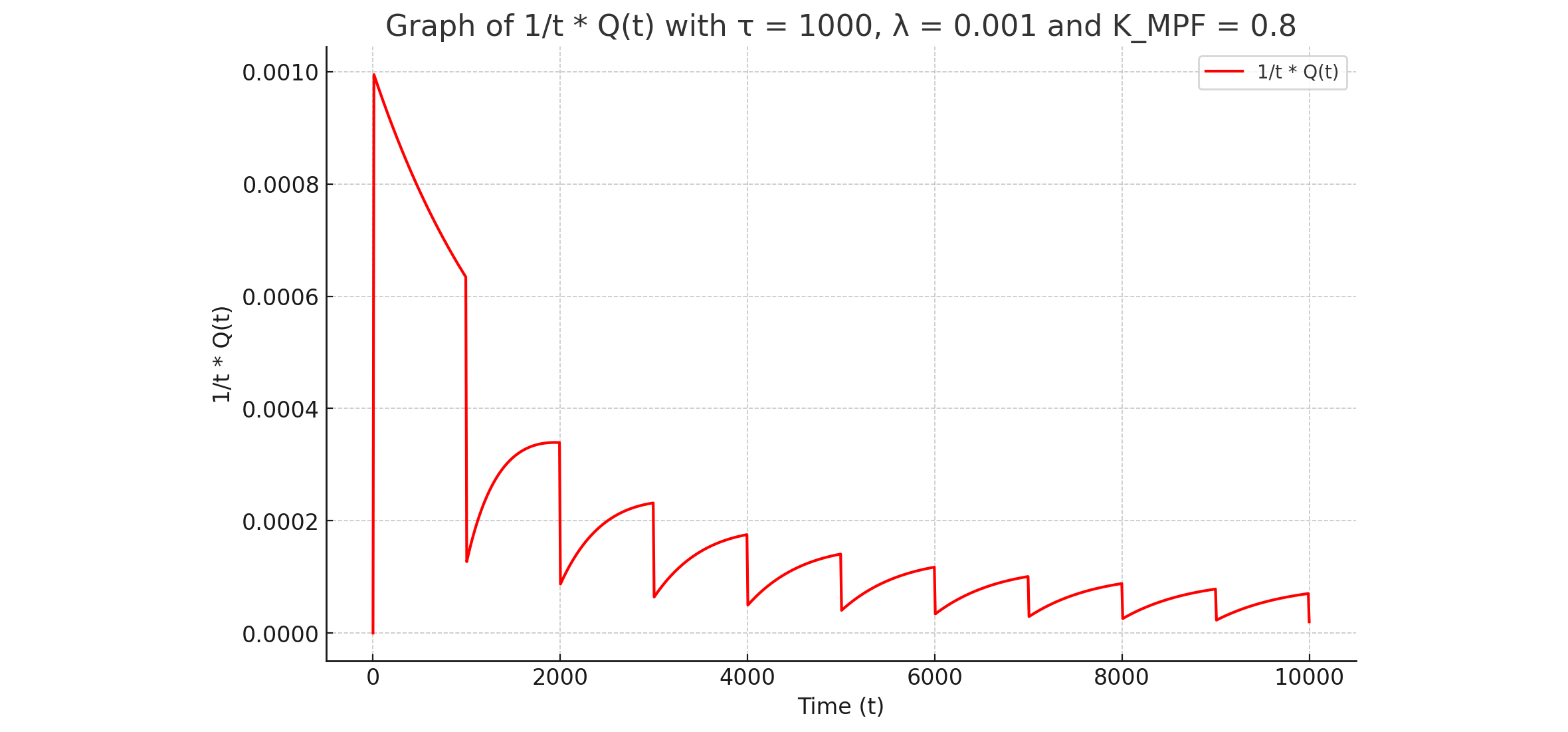
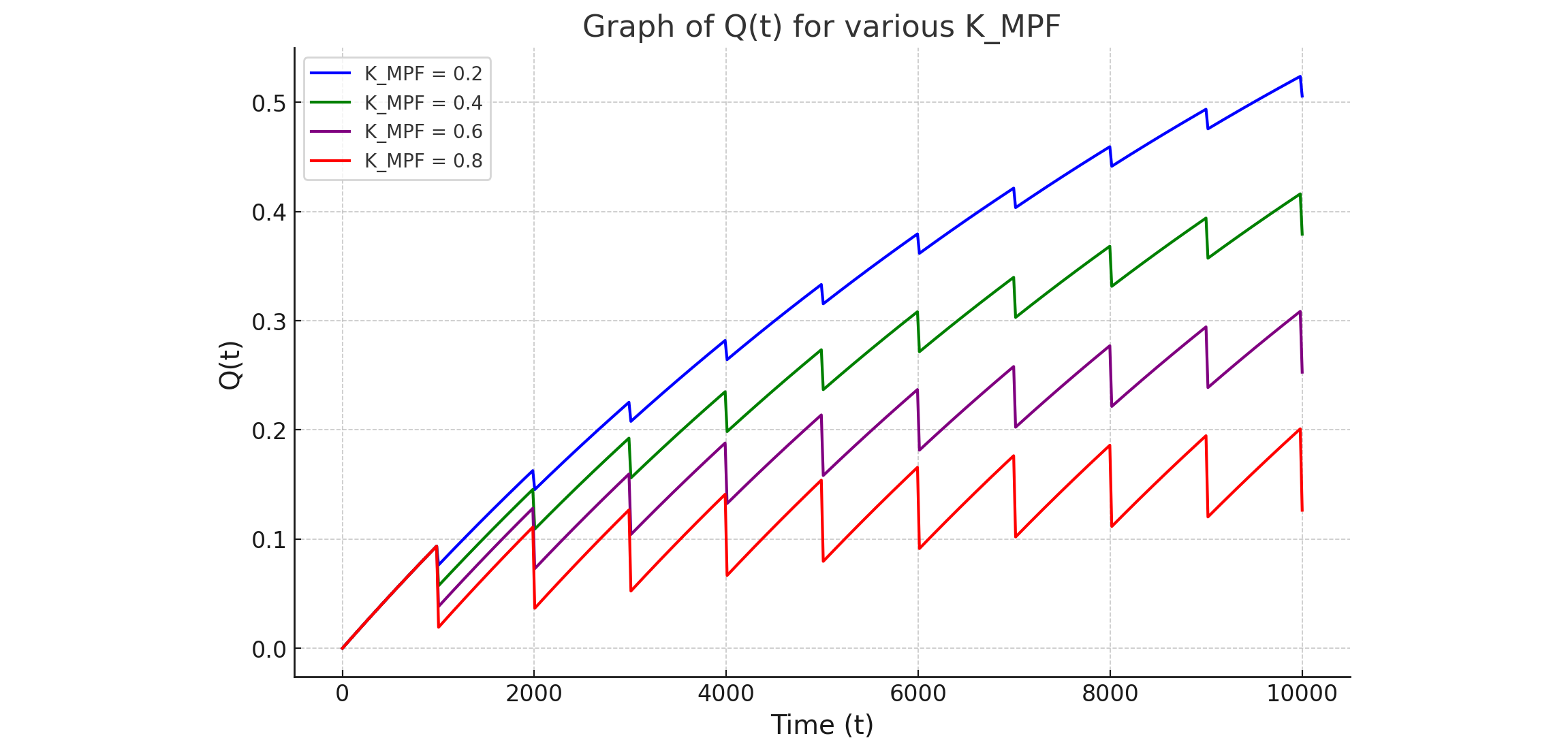
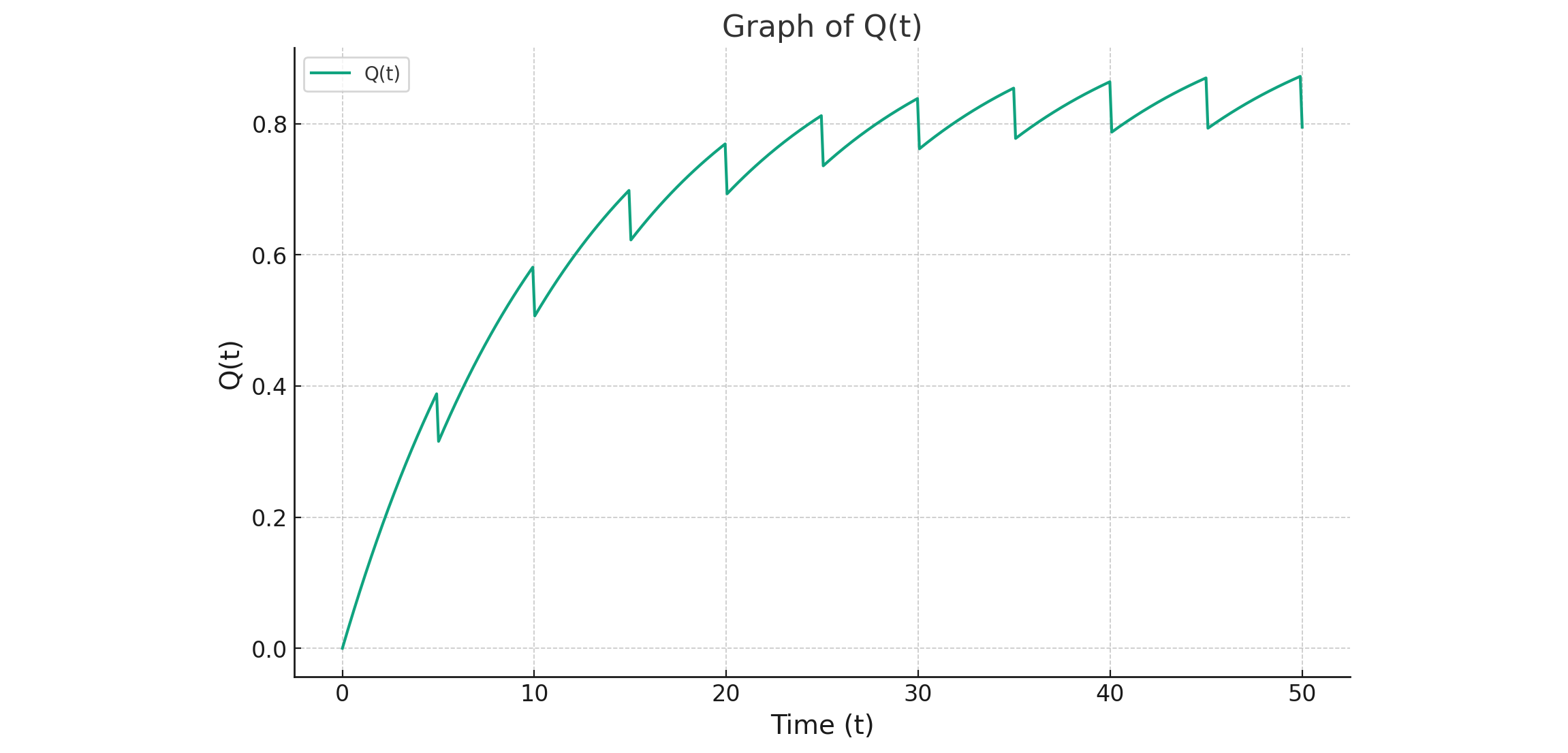
$Q(t)$とChatGPT (24) |
 |
さらに、過去記事で8通りの事象の分類からの$Q_\text{SM}(t)$導出を実施しましたが、これをChatGPT-4に実行させてみます。
人間:
ISO 26262の範囲では故障率λは一定値をとると考える。従って、フォールトの分布は指数分布となります。
一般にはSM (Safety Mechanism)にフォールトが起きても直ちにVSG(Violation of a safety goal)とならないため、意図機能が動作している間に修理が可能であり、これをリペアラブルエレメントと言います。SMの故障率は$\lambda_\text{SM}$です。
定期検査修理スキームは以下のとおりです。2nd SMによるSMに対する定期検査が、周期$\tau$で行われます。 i番目の検査時刻は$\tau i, i=1,...,n$とするとき、最近の検査時刻を$τ_n$とすれば、$τ_n=nτ=\lfloor\frac{t}{\tau}\rfloor\tau$
定期検査により検出されたフォールトは全て、瞬時に修理されるものとします。ここで検査は確定的に実施されるため、区間$[(i-1)\tau, i\tau)$で生起した検出されるフォールトは全てiτにおいて修理されます。
SMのフォールト生起について、((0から$\tau_n$までの生起の有/無),($\tau_n$での検出の可/不可),($\tau_n$から$t$までの生起の有/無)) の8通りについて考え、$t$において不稼働の事象を洗い出してください。
なお、$\tau_n$での故障検出可とは、故障の有無を問わないものとします。一例として、故障が無いから検出できないとするのではなく、SMのうち検出可部分の故障が無いと読みます。この場合は故障の生起は無し、検出は有りとします。
ChatGPT: (中略)
指定されたシステムについて、フォールトの生起と検出に関連する8つの異なる事象を考えます。以下の条件を考慮して、不稼働の事象を洗い出します。
- $ 0 \leq t < \tau_n $: この区間では故障の検出は行われません。
- $ \tau_n \leq t < \tau_{n+1} $: この区間では故障が発生しても、次の検査時刻まで検出されません。
以下の8通りの事象を考えます。
- $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起なし
- $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起あり
- $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出可、$ (\tau_n,t) $での故障生起なし
- $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出可、$ (\tau_n,t) $での故障生起あり
- $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起なし
- $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起あり
- $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出可、$ (\tau_n,t) $での故障生起なし
- $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出可、$ (\tau_n,t) $での故障生起あり
したがって、不稼働の事象は以下の5つとなります。
- 事象2: $ (0,\tau_n) $での故障が生起しないものの、$ (\tau_n,t) $で故障が生じ、そのまま不稼働となる。
- 事象4: $ (0,\tau_n) $での故障が生起しないものの、$ (\tau_n,t) $で故障が生じる。この故障は$ \tau_n $で検出可能であったにも関わらず、次の検査まで検出されない。
- 事象5: $ (0,\tau_n) $での故障が検出されず、$ \tau_n $での検出もなく、そのまま不稼働となる。
- 事象6: $ (0,\tau_n) $での故障が検出されず、$ (\tau_n,t) $でさらに故障が生じ、不稼働となる。
- 事象8: $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出可(瞬時に修理される)、$ (\tau_n,t) $での新たな故障生起あり(不稼働へ)
ご指摘いただいた内容を踏まえて、不稼働の事象は上記の5つとなります。再度ご確認いただけますでしょうか。
人間:
正解です。$t$においてSMが不稼働になる条件について、検出の可・不可にで大分類し、検出の可否とフォールトの生起区間の2つの事象の積にそれぞれ分解してください。 これはフォールトの生起と検出の可否が独立であるため可能です。 さらにフォールト生起区間を合成してください。合成とは、例えばフォールト生起区間$[t1, t2)$または$[t2, t3)$の事象を$[t1, t3)$とすることを意味します。
ChatGPT:
指定された条件に基づき、SMが不稼働になる条件を検出の可・不可によって大分類し、それぞれの事象を分解します。その後、フォールト生起区間を合成します。
検出不可の場合
検出不可の場合の不稼働事象は以下の3つでした。
- 事象2: $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起あり
- 事象5: $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起なし
- 事象6: $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出不可、$ (\tau_n,t) $での故障生起あり
フォールト生起区間の合成
- $ (0,\tau_n) $または$ (\tau_n,t) $の区間での故障生起
検出可の場合
検出可の場合の不稼働事象は以下の2つでした。
- 事象4: $ (0,\tau_n) $での故障生起なし、$ \tau_n $での検出可、$ (\tau_n,t) $での故障生起あり
- 事象8: $ (0,\tau_n) $での故障生起あり、$ \tau_n $での検出可(瞬時に修理)、$ (\tau_n,t) $での新たな故障生起あり
フォールト生起区間の合成
- $ (\tau_n,t) $の区間での故障生起
結論
- 検出不可の場合:フォールト生起区間が$ (0,\tau_n) $または$ (\tau_n,t) $であれば、SMが不稼働になる可能性がある。
- 検出可の場合:フォールト生起区間が$ (\tau_n,t) $であれば、SMが不稼働になる可能性がある。
以上が、指定された条件に基づく不稼働の事象の分析です。
人間:
結論の時間区間を簡略化してください。
ChatGPT:
もちろんです。結論の時間区間を簡略化すると、以下のようになります。
- 検出不可の場合:フォールト生起区間が $ (0,t) $ であれば、SMが不稼働になる可能性がある。
- 検出可の場合:フォールト生起区間が $ (\tau_n,t) $ であれば、SMが不稼働になる可能性がある。
検出不可の場合では、検出が行われないため、全体の時間区間 $ (0,t) $ での故障生起が不稼働の条件となります。検出可の場合は、検出されれば修理されるため、$ \tau_n $ 以降の新たな故障生起が不稼働の条件となります。
うまく誘導した結果、正解の条件を導出しました。