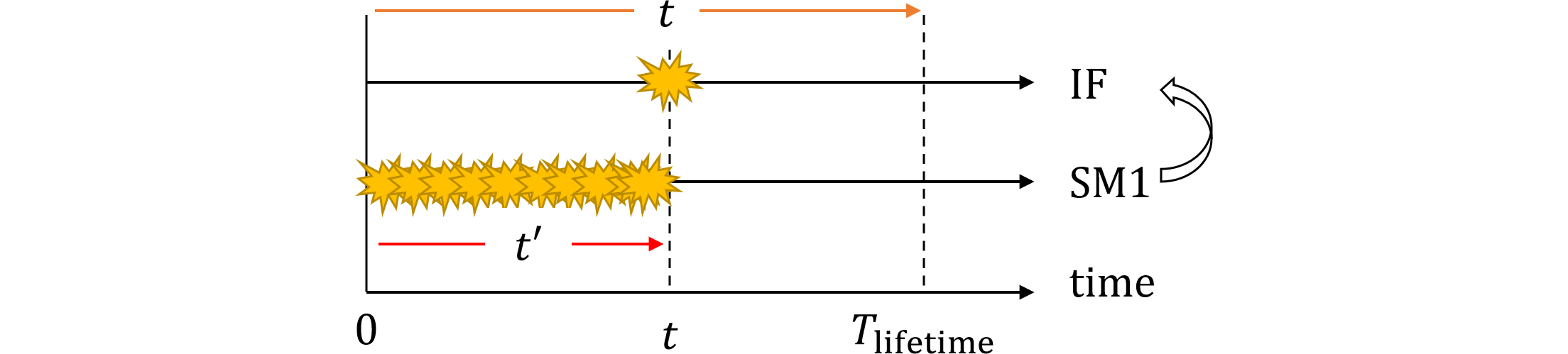
ここまでで規格解説書方式と弊社CTMCベースでは積分順序に違いがあることがわかります。パターン1はフォールトの生起はSM1⇒IFの順であり、かつSM1のフォールトはSM2により検出されず、全量レイテントとなる場合です。表479.1に示すように規格解説書の方式は、積分順序がフォールト生起とは逆順です。
表479.1
| パターン1 |
フォールト
生起順序 |
積分順序 |
| 規格解説書方式 |
SM1⇒IF |
IF⇒SM1 |
| 弊社CTMC方式 |
SM1⇒IF |
規格解説書方式
規格解説書によればPoF(Probability of Failure)は、
$$
PoF_\text{SM1,lat⇒IF}=\int_0^{T_\text{lifetime}}f_\text{SM1,DPF,lat}(t)\left[\int_t^{T_\text{lifetime}}f_\text{IF,DPF}(t')dt'\cdot R_\text{IF}(t)\right]dt
\tag{479.1}
$$
と記載されています。その意味は図479.1で示すように、時刻$t$から車両寿命まで、後フォールトであるIFに関する積分を先に実行し、後から先フォールトであるSM1の積分を実行しています。
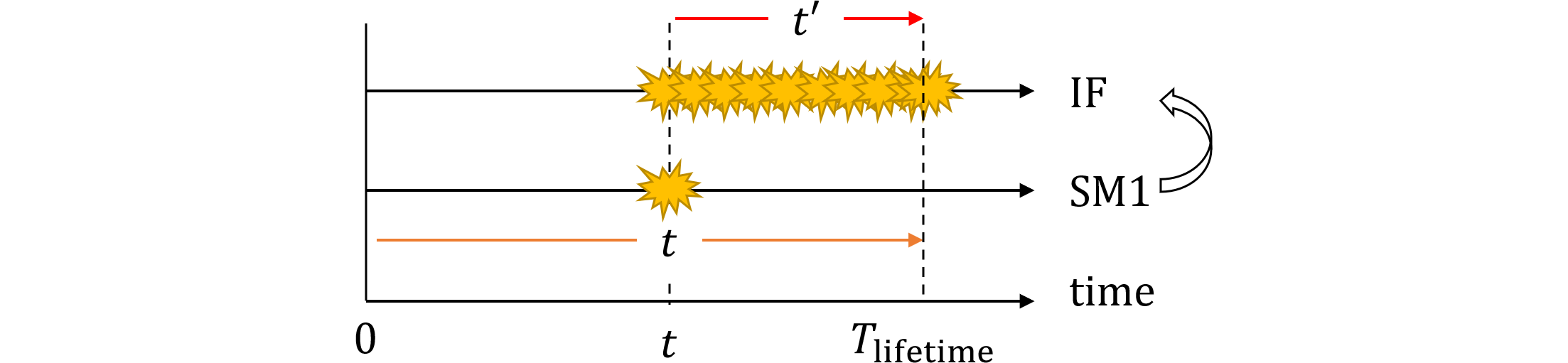図479.1 規格解説書方式
2つの定数
$$
\begin{eqnarray}\begin{cases}
f_\text{SM1,DPF,lat}(t)=(1-K_\text{SM1,DPF})f_\text{SM1}(t)\\
f_\text{IF,DPF}(t')=K_\text{IF,DPF}f_\text{IF}(t')
\end{cases}\end{eqnarray}\tag{479.2}
$$
を用いて書き換えます。まず(479.1)を車両寿命で時間平均したものがPMHFであるから
$$
M_\text{PMHF,com,P1}=\frac{1}{T_\text{lifetime}}PoF_\text{SM1,lat⇒IF}\\
=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})
\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\cdot R_\text{IF}(t)\right]dt
\tag{479.3}
$$
と書き換えられます。規格解説書の導出において条件付き確率を用いていない誤りがあるため、まずそれを修正した上でPMHF式を導出します。
第1の誤り
(479.3)は[]内のIFについての積分に2か所誤りが有ります。まず、「IFが時刻$t$までup」という条件
$R_\text{IF}(t)$がかけられていますが、IFのフォールト時刻は図479.1より時刻$t'$であるため、IFは$t'$までupでなければなりません。従って、
$$R_\text{IF}(t)⇒R_\text{IF}(t')$$
と修正します。
$R_\text{IF}(t)$を用いることもできますが、さらに「IFが時刻$t$までupという条件下で時刻$t'$までup」という条件付き確率をかける必要があります。そうしないと時刻$t$から$t'$までの変化を無視してしまいます。条件付き確率の公式
$$
\Pr\{A|B\}=\frac{\Pr\{A\cap B\}}{\Pr\{B\}}
$$
を用れば、
$$
\require{cancel}
\Pr\{\text{IF up at }t\}\cdot\Pr\{\text{IF up at t'}|\text{IF up at }t\}=\bcancel{R_\text{IF}(t)}\cdot \frac{R_\text{IF}(t')}{\bcancel{R_\text{IF}(t)}}=R_\text{IF}(t’)
$$
となり、前述のように$R_\text{IF}(t)$⇒$R_\text{IF}(t')$と修正したのと同じことになります。
第2の誤り
2点目は$f_\text{IF}(t')$が誤りです。IFのupとdownの事象は独立ではないので、これは「IFが時刻$t'$までupという条件下で$t'$から$t'+dt'$までの間にIFがフォールトする」という条件付き確率でなければなりません。
そのため、(66.4)の確率密度関数ではなく(66.8)の故障率をかける必要があります。従って、
$$
f_\text{IF}(t')dt'⇒\lambda_\text{IF}dt'
$$
と修正します。
パターン1のPMHFの導出
上記の誤り2点を修正すれば(479.3)は、
$$
M_\text{PMHF,com,P1}=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})
\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[\int_t^{T_\text{lifetime}}R_\text{IF}(\color{red}{t'})\cdot\color{red}{\lambda_\text{IF}}dt'\right]dt\\
=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})
\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\right]dt\\
=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})
\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[F_\text{IF}(T_\text{lifetime})-F_\text{IF}(t)\right]dt\\
=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})\left[F_\text{IF}(T_\text{lifetime})F_\text{SM}(T_\text{lifetime})-
\int_0^{T_\text{lifetime}}f_\text{SM1}(t)F_\text{IF}(t)dt\right]\quad\quad\color{red}{※}\\
\approx K_\text{IF,DPF}(1-K_\text{SM1,DPF})\left[\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}-
\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_\text{SM1}(t)F_\text{IF}(t)dt\right]\\
=\img[-1.35em]{/images/withinseminar.png}
\tag{479.4}
$$
と求められます。導出には公式(60.6)を使用しました。
若干気持ち悪いのは、フォールト順がSM1⇒IFであるのに対して、積分順序が逆順になっていることです。(479.4)$\color{red}{※}$行を見ても、SM1⇒IFの確率を求めるのにあたり、DPF確率全体$F_\text{IF}(T_\text{lifetime})F_\text{SM}(T_\text{lifetime})$から逆順であるIF⇒SM1の確率を引いており、straight forwardではありません。
本稿では上記2点の誤りを修正しましたが、結果として解説書の方式でも結果は変わりません。従って、これらはマイナーな誤りと判定します。
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。
前のブログ
次のブログ
