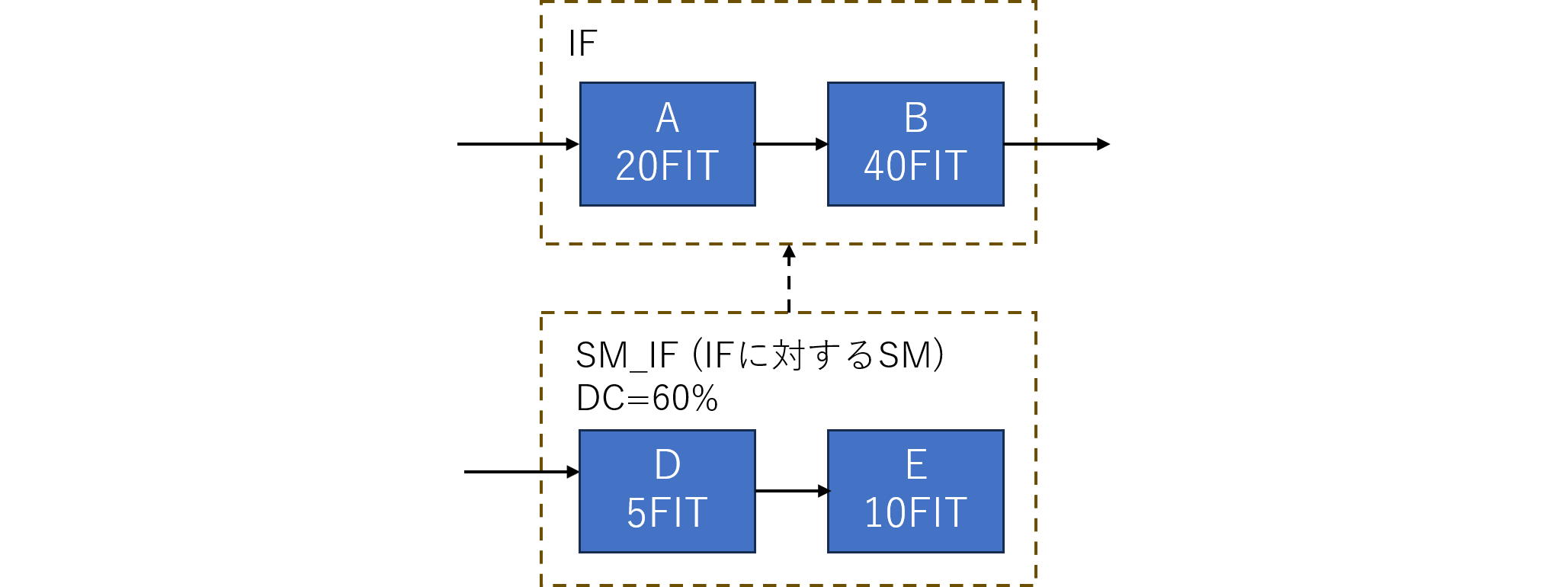
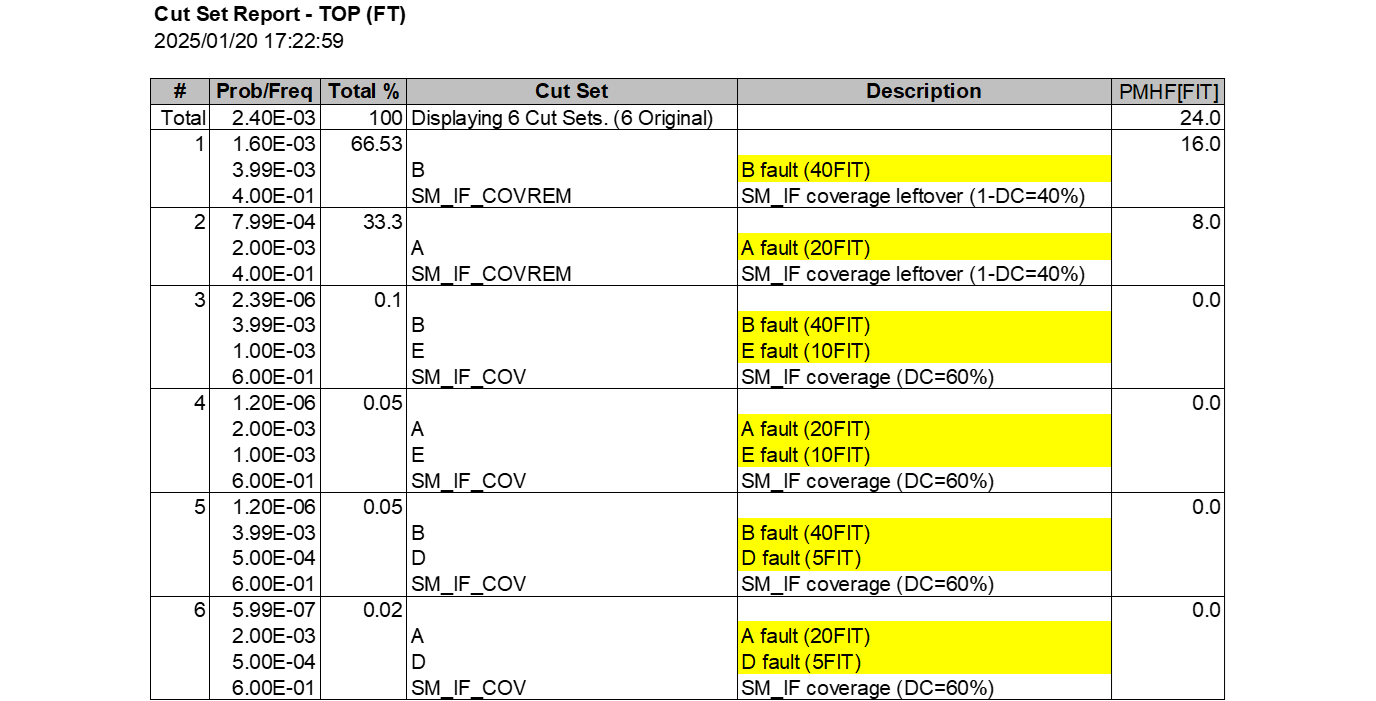
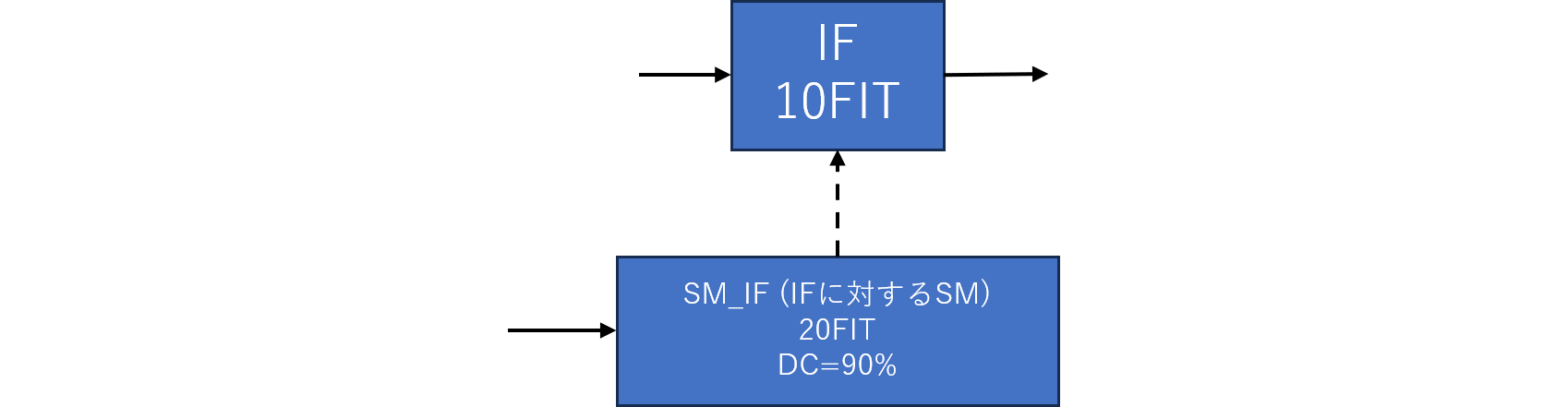
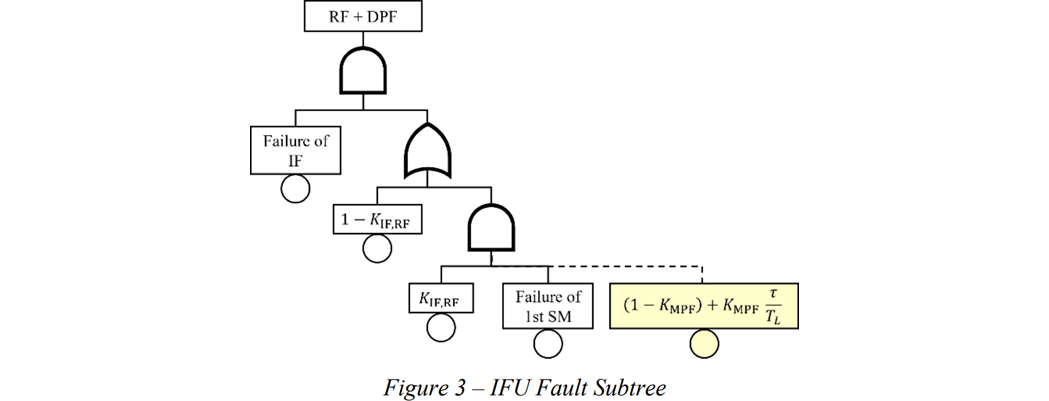
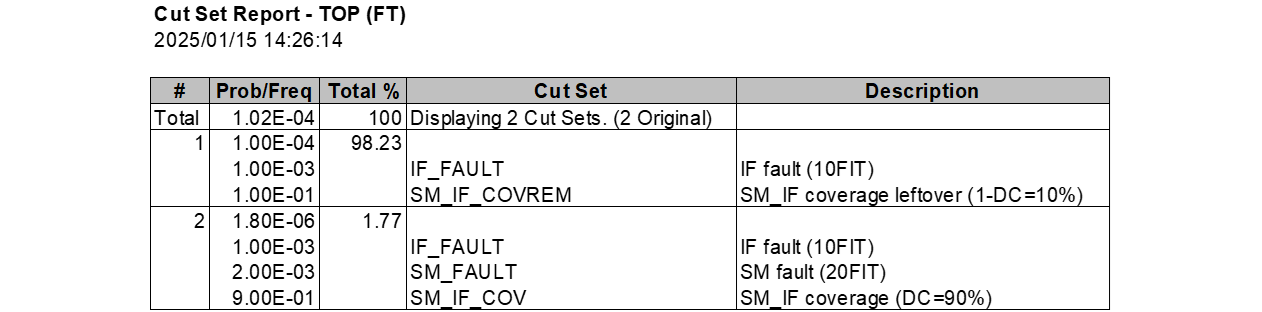
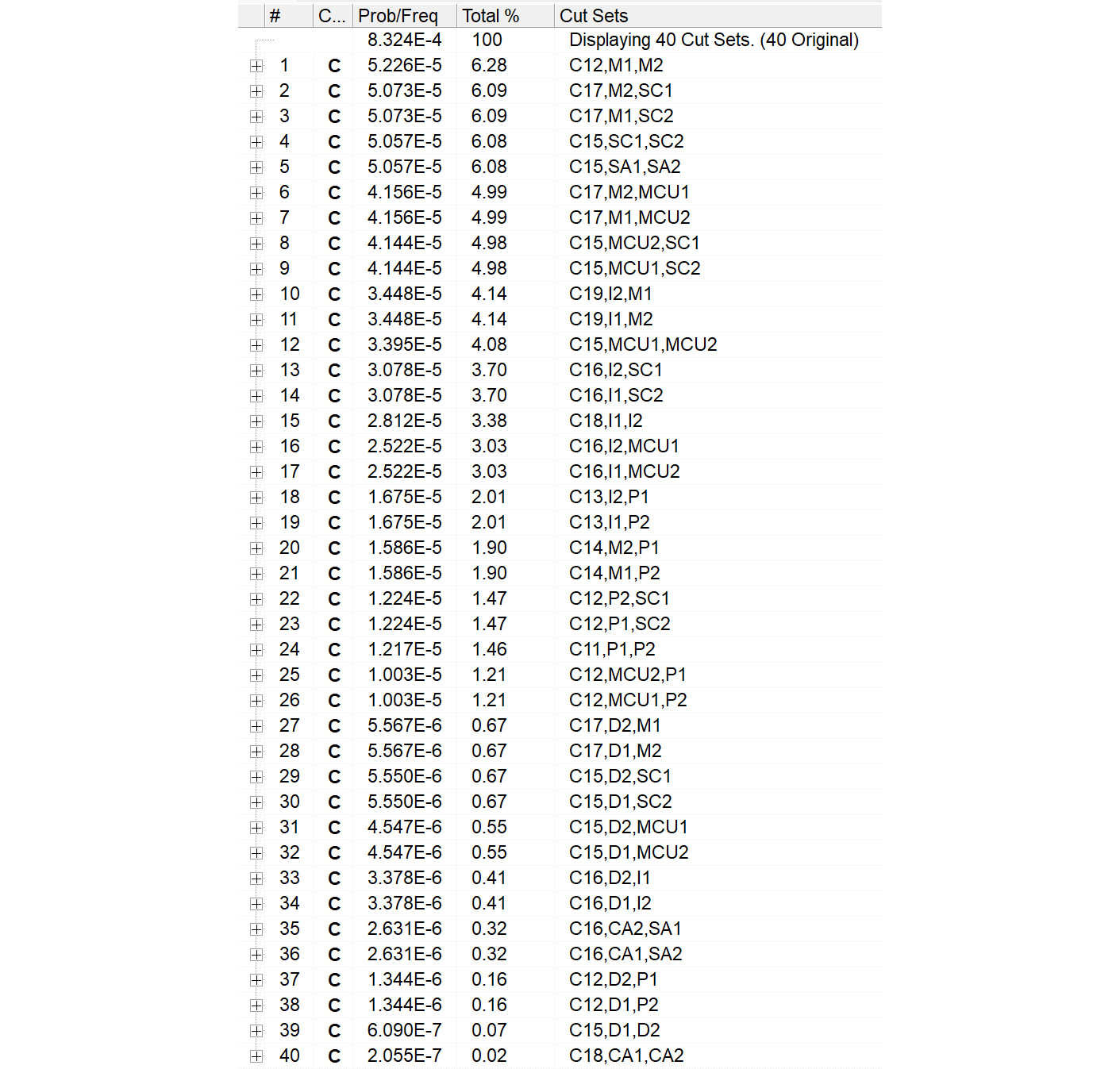
Method 3に向けてChatGPT-o1 proに作成させたpythonプログラムを示します。これは各エレメントの故障率及び2nd SMによるカバレージに基づき、FTを構成するファイル群MARDを生成するプログラムです。
#!/usr/bin/env python3
import math
# 1) 各要素のFIT(λ)およびカバレッジDC
FIT_map = {
"P": 2.33e-7,
"MCU": 8.18e-7,
"D": 1.09e-7,
"I": 5.99e-7,
"M": 1.00e-6,
"SC": 1.00e-6,
"CA": 5.10e-8,
"SA": 1.00e-6,
}
DC_map = {
"P": 0.00,
"MCU": 0.99,
"D": 0.99,
"I": 0.60,
"M": 0.90,
"SC": 0.99,
"CA": 0.60,
"SA": 0.99,
}
# 上流G11,G21 => 36ペア, 下流G12,G22 => 4ペア 合計40
G11 = ["P1","MCU1","D1","I1","M1","SC1"]
G21 = ["P2","MCU2","D2","I2","M2","SC2"]
G12 = ["CA1","SA1"]
G22 = ["CA2","SA2"]
T_mission = 1.5e4 # 15000h
tau_over_TL = 3420.0/15000.0 # 0.228
def lam(e):
""" Return FIT value (lambda) for e (e.g. 'M1' -> base 'M'). """
return FIT_map[e[:-1]]
def DC(e):
""" Return DC coverage for e. """
return DC_map[e[:-1]]
def factor_method3(e1,e2):
""" Compute factor(4桁丸め前) for handout(手法3):
base = (1-DC(e1))*(1-DC(e2))
factor = base + (1-base)*tau_over_TL
"""
base = (1 - DC(e1)) * (1 - DC(e2))
return base + (1.0 - base)*tau_over_TL
def all_pairs():
""" 全40ペア: 上流36 + 下流4 """
idx=0
for x in G11:
for y in G21:
idx+=1
yield idx,x,y
for x in G12:
for y in G22:
idx+=1
yield idx,x,y
# 2) 40ペアの計算
pairs = []
for (i,e1,e2) in all_pairs():
pairs.append((i,e1,e2))
pairs.sort(key=lambda x:x[0])
# coverage factorを 4桁丸めでユニーク管理し、C11 から順番付与
coverage_map = {} # dict: factor_4 -> coverage_name
coverage_list = [] # list to store (coverage_name, factor_4)
def coverage_name_for(f4):
""" 4桁丸めした factor f4 に対応する coverage 名を割当。
最初に出たfactorにはC11、その次C12…
"""
if f4 in coverage_map:
return coverage_map[f4]
# 次のインデックス
idx = len(coverage_map) # 0-based
cname = f"C{idx+11}" # e.g. if idx=0 => 'C11', idx=1 => 'C12', ...
coverage_map[f4] = cname
coverage_list.append( (cname, f4) )
return cname
results = []
for (i,e1,e2) in pairs:
raw_factor = factor_method3(e1,e2) # not rounded yet
f4 = round(raw_factor,4) # 4桁丸め
c_name = coverage_name_for(f4)
results.append( (i,e1,e2,raw_factor,f4,c_name) )
results.sort(key=lambda x:x[0])
# 各BasicEvent
basic_events = [
"P1","MCU1","D1","I1","M1","SC1","CA1","SA1",
"P2","MCU2","D2","I2","M2","SC2","CA2","SA2"
]
def lam_str(e):
""" return lam in 3E format """
l = lam(e)
return f"{l:.3E}"
def unreli(e):
""" 1-exp(-lam*T_mission) """
l= lam(e)
import math
return 1.0 - math.exp(-l*T_mission)
# 3) 5ファイルを出力
# METHOD3.BED, METHOD3.BEI, METHOD3.FTD, METHOD3.FTL, METHOD3.GTD
bed_lines = []
bei_lines = []
ftd_lines = []
ftl_lines = []
gtd_lines = []
# 3.1 BED
bed_lines.append("*Saphire 8.2.9\nTEST =")
bed_lines.append("* Name , Descriptions , Project")
for be in basic_events:
bed_lines.append(f"{be} , {be}desc , TEST")
for (cn,f4) in coverage_list:
bed_lines.append(f"{cn} , CoverageFactor_{cn} , TEST")
# 3.2 BEI
bei_lines.append("*Saphire 8.2.9\nTEST =")
bei_lines.append("* Name ,FdT,UdC,UdT,UdValue,Prob,Lambda,Tau,Mission,Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project")
# basic events
for be in basic_events:
l = lam(be)
l_str = f"{l:.3E}"
un = unreli(be)
un_str = f"{un:.3E}"
# FdT=3 => exp. dist, prob => un
line = f"{be} ,3, , ,0.000E+000,0.000E+000,{l_str},0,1.500E+004, , ,0.000E+000,{un_str}, ,RANDOM,CD,TEST"
bei_lines.append(line)
# coverage
for (cn,f4) in coverage_list:
f_str = f"{f4:.4E}"
line = f"{cn} ,1, , ,0.000E+000,{f_str},0.000E+000,0,0.000E+000, , ,0.000E+000,{f_str}, ,RANDOM,CD,TEST"
bei_lines.append(line)
# 3.3 FTD
ftd_lines.append("TEST =")
ftd_lines.append("* Name , Description, SubTree, Alternate, Project")
ftd_lines.append("METHOD3 ,Method3TopDefinition, , ,TEST")
# 3.4 FTL
ftl_lines.append("TEST,METHOD3 =")
mcsnames = [f"MCS{i:02d}" for i in range(1,41)]
mcs_line = " ".join(mcsnames)
ftl_lines.append(f"METHOD3 OR {mcs_line}")
for (i,e1,e2,rawf,f4,cname) in results:
mcs = f"MCS{i:02d}"
ftl_lines.append(f"{mcs} AND {e1} {e2} {cname}")
# 3.5 GTD
gtd_lines.append("TEST=")
gtd_lines.append("* Name , Description, Project")
gtd_lines.append("METHOD3 ,Method3TopGate, TEST")
for i in range(1,41):
gtd_lines.append(f"MCS{i:02d} ,Pair{i:02d}, TEST")
# ---- Write out actual files ----
def write_file(fname, lines):
with open(fname, "w", encoding="utf-8") as f:
for ln in lines:
f.write(ln+"\n")
write_file("METHOD3.BED", bed_lines)
write_file("METHOD3.BEI", bei_lines)
write_file("METHOD3.FTD", ftd_lines)
write_file("METHOD3.FTL", ftl_lines)
write_file("METHOD3.GTD", gtd_lines)
print("Created METHOD3.BED, METHOD3.BEI, METHOD3.FTD, METHOD3.FTL, METHOD3.GTD successfully.")
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です。
 前のブログ
次のブログ
前のブログ
次のブログ