|
3 |
Pipeline processorの設計 (2) |
機械の場合
人間であれば器用に3つの処理を一人で実行することができますが、コンピュータは機械なので一つのことしかできません。つまり、A専用、B専用、C専用の3つの機械を並べて処理することになります。
- 社内メール封筒を取りに行く ----- A専用機
- 宛名を書いて書類を入れて封をする ----- B専用機
- 社内メール投函箱に投函しに行く ----- C専用機
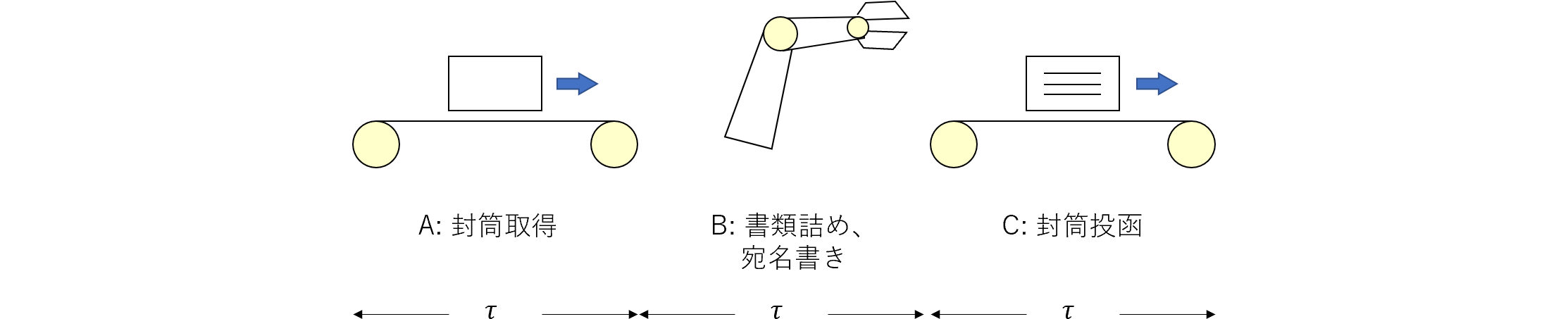
レイテンシは前稿の3人がかりと同じように$3\tau$で、スループットはその逆数である$\frac{1}{3\tau}$です。これを表452.1にまとめます。
| 個別/全体 | レイテンシ | スループット |
|---|---|---|
| A, B, C個別 | $\tau$ | $\frac{1}{\tau}$ |
| A+B+C全体 | $3\tau$ | $\frac{1}{3\tau}$ |
パイプライン化
さて、ここでシステムのスループット(システム性能)は$\frac{1}{3\tau}$ですが、その向上を考えてみます。
性能向上のためレイテンシ短縮を考えると、$3\tau$以下にするのは困難です。ところが、AとB、BとCの間に箱を置いて、$3\tau$ではなく、$\tau$毎に処理を入力したらどうでしょうか。ちょうどバケツリレーのように$\tau$毎に処理が可能です。
スループットから見てみましょう。元々A, B, Cの機械単体でのスループットは$\frac{1}{\tau}$だったのですが、システムで組み合わせると$\frac{1}{3\tau}$のように33%に低下していました。
例えばA機械は、BとCが働いているときには遊んでいたわけです。これを間に箱を入れて切り離すようにした結果、レイテンシはほとんど変わらずに、スループットは3倍の100%に向上しました。つまり、A, B, Cそれぞれの機械の能力を100%出し切ることができたわけです。
| 個別/全体 | レイテンシ | スループット |
|---|---|---|
| A+B+C全体をパイプライン化 | $3\tau$ | $\frac{1}{\tau}$ |
このように、パイプライン化はあまりコストをかけることなく、性能を大幅に向上できる特長があります。一般的には、全体を$n$ステージのパイプラインで構成すれば、レイテンシはあまり変わらず$n\tau+\alpha$と若干増加するだけです。一方、スループット(性能)を$n$倍のように大幅に引き上げることができます。
