共通原因故障(CCF)

前稿では冗長制御方式を取り上げて、メインマイコンとサブマイコンがお互いに主機能とSMの関係になっており、SPFを防止していることを説明しました。共通原因故障(Common Cause Failure, CCF)が無い理想的な場合にはこれが成立します。一方、メインマイコンとサブマイコンにCCFを持つ場合にはどうなるか、MCSを取得してみましょう。

CCFの例

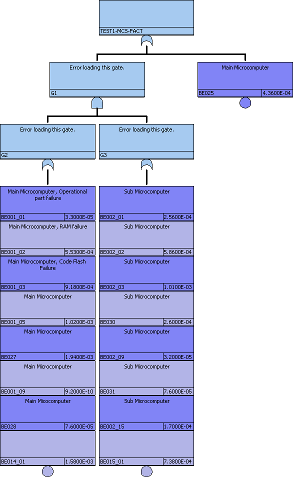
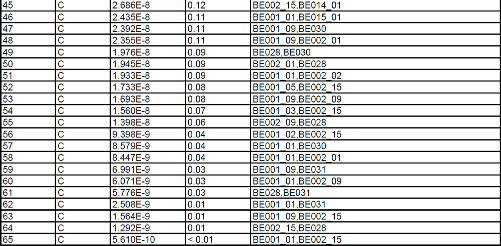
メインマイコンとサブマイコンに共通の発振回路からクロックを供給している場合はどうでしょうか？ メインマイコン発信回路の故障をBE028、サブマイコン発振回路の故障をBE031としていたもとのツリーを変更してBE031をBE028に置き換えてみます。こうすると冗長系の両側に共通の故障原因BE028を持つことになり、MCSを取得すると以下のようにANDの下だったものが上位のORに接続され、SPFの原因となります(図29.1)。

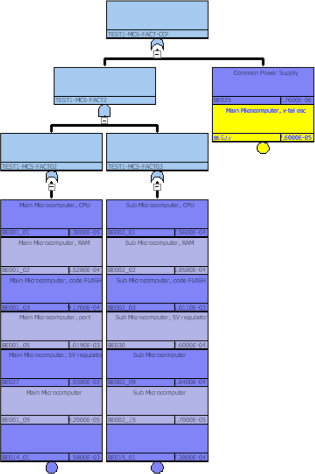
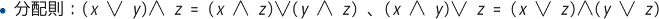
図29.2はブール代数の分配則であり、これにより上記論理変換が行われます。

これは何を意味するかというと、共通の電源、クロック源、あるいは共通の型番を持つと、単一のランダムハードウェア故障ないしはシステマティック故障により、メインマイコンとサブマイコンのお互いの安全機構の構造が崩れて、単一原因により安全目標が侵害されるとことになり、重要な故障となることを意味します。

ISO26262はこのCCFを定量的に計算する手段を規定していないため、ISO26262のベース規格であるIEC61508に記述されているCCFのβファクタを援用することになります。また、ISO26262の発展規格であるISO19451において、従属故障分析(DFA, Dependent Failure Analysis)として詳述されていますので、ご参照ください。

前のブログ 次のブログ

因数分解

前稿のMCSにおいて因数分解を行います。このステップは必須のステップではありません。論理的には前のツリーと等価なツリーなのですが、冗長構成となっていることをひとめで明らかにするために因数分解を行います。上記のMCS論理式を因数分解したものを以下のFTに示します。因数分解はAND-OR形式をOR-AND形式に変換するものですが、残念ながら自動的には困難であるため、人力で行います。

論理等価なのでMCSは上記MCSと同じです。メインマイコン各部(8箇所)の故障とサブマイコン各部(8箇所)の故障が互いに主機能・安全機構の関係となりSPFを防止しており、共通部分の回路のみがSPFとなっていることがひとめでわかります。MCの数は前と同じく8×8+1=65項となります。

ISO26262の目的は安全に関する論証なので、このようにアセッサー等の第三者が見てわかりやすいドキュメントを生成することが重要です。マイコンやLSIのように比較的故障率の大な部品を使用する際に、マイコン単体でASIL-Dを達成するのは困難ですが、このような冗長構成をとればSPF/RFが冗長部分で微小となるため、ASIL-D対応が可能となります。

前のブログ 次のブログ

実際の例

システムFTAの実例をご紹介します。これはあるECUの安全分析を実施したもので、メインマイコンとサブマイコンによる冗長制御を行っているECUの例です。電源回路は共通で、共通の信号が両マイコンに入力され、両マイコンの出力が揃って初めて動作するという回路構成となっています。主機能としてはマイコンはひとつで成立するのですが、ECUがASIL-D対応をする必要があるため、冗長構成をとり故障率を低減しています。

システムFTAと称する理由は、基事象が部品の故障モードではなく、エレメントの故障モードとなっているためです。

トップ事象を侵害する分析は、このように一般的に非常に複雑になり、マイコンの故障が複数個所に出てくることになります。以下はFTの図です。

MCSの導出

この例のMCSを取得したものが以下の図です。SAPHIREにより155個の積項(ミニマルカット=MC)が得られました。カラムは順番に、その事象の「連番」、「ケース」、「確率」、「確率のパーセント表記」、「ミニマルカット」です。

3次以上の次数項の省略

次にSAPHIREの分析の際に、3次以上の積項を省略したMCSを取得してみます。3次以上の積項を省略する理由は、ISO26262において3点故障はセーフフォルトとして良いとあるためであり、3次以上の積項は一般的に確率的に非常に小さいので省略可能なためです。

これを行うにはSAPHIREにおいて、Fault Treeを選択しSolveコマンドを実行する際に、Sizeに2を設定します。すると155個得られた積項が65個と減少します。以下のMCSの論理式を確認すると1次と2次の積項のみであることがわかります。今回はTOP事象の侵害確率は、155項の積算でも65項の積算でも2.218E-5と変わりませんでした。これからも3次以上の積項を省略することが可能と言えます。

これを論理式として出力し、FTL(Fault Tree Language)に(手で)変換してからSAPHIREに取り込むと、SAPHIREがツリーを構成してくれます。その図を以下に示します。

前のブログ 次のブログ