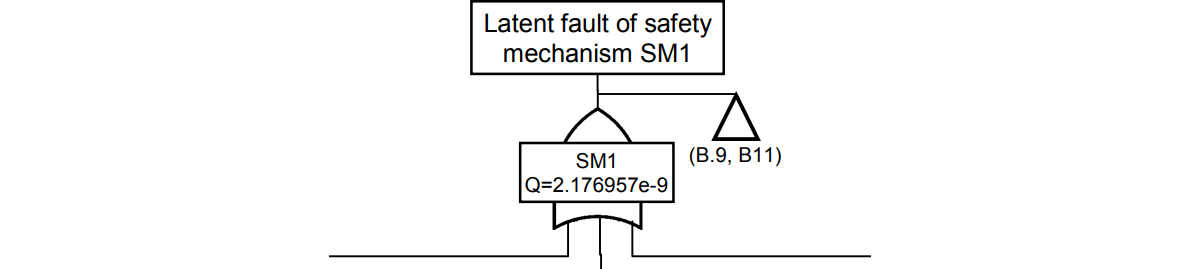
次にSM1のフォールトが、2nd SMであるSM2により検出可能にもかかわらずLFとなる確率を示すANDゲートです。

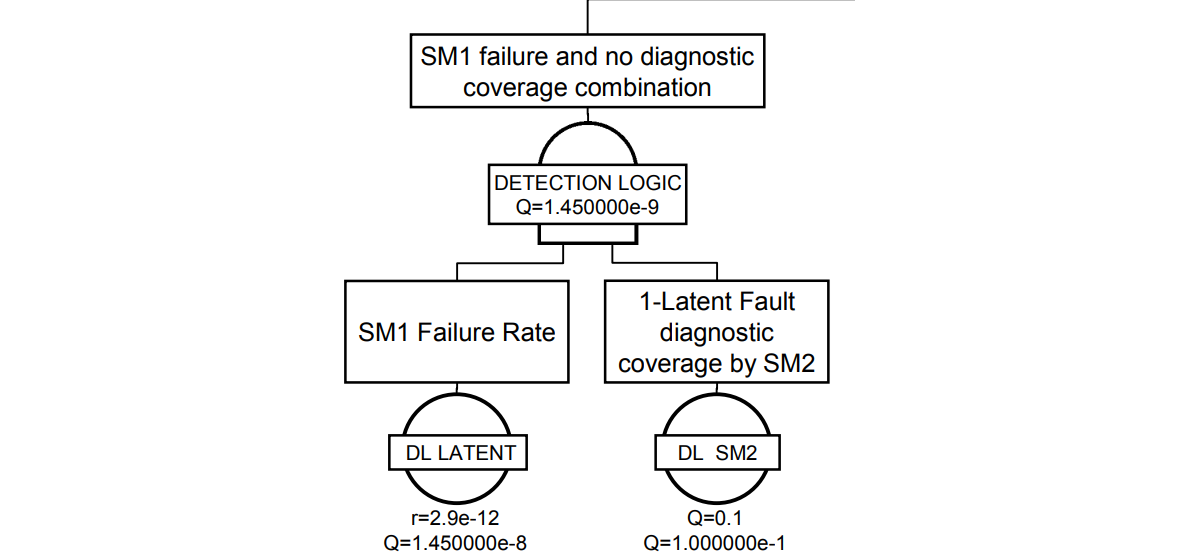
SM2によりSM1のフォールトが検出されない部分は前ページのツリーでした。このページはSM2によりSM1のフォールトが100%検出される部分なので、基本的にはLFにはならないように思われます。実は、SM2の検査周期以内ではSM1のフォールトの検出できないことから、微小な確率が残ります。

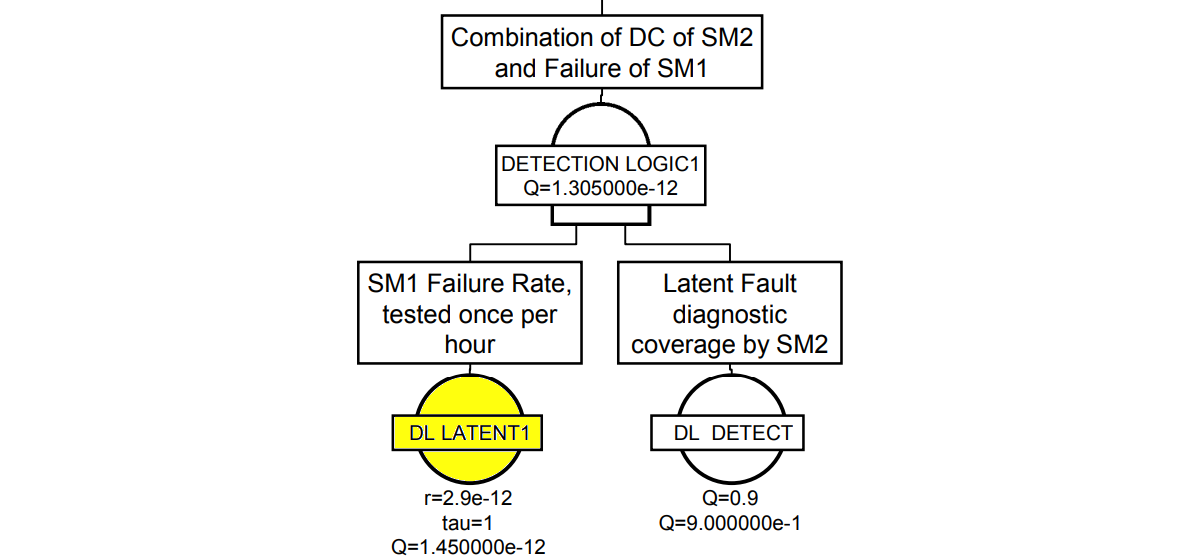
ANDゲートの左下の事象はSM1のフォールトが検査周期内にフォールトする確率です。故障率に掛ける時間がデフォールトのミッションタイムである車両寿命ではなく、特殊なミッションタイムである検査周期となるため、注意喚起のため本記事でのみ、事象を黄色で塗っています。そのため事象には、故障率$\lambda_\text{SM1}$だけでなくミッションタイム$\tau$も入力します。計算では以下のように$\frac{1}{2}$をかけているようで、確率は $$ \require{color} \definecolor{pink}{rgb}{1.0,0.8,1.0} Q=\frac{1}{2}\lambda_\text{SM1}\tau=\colorbox{pink}{0.5(?)}\cdot2.9\times10^{-12}\cdot1=1.45\times10^{-12}\tag{589.1} $$ となっています。0.5の理由は不明です。

ANDゲートの右下の事象はSM2によるレイテントフォールトカバレージで、$DC_\text{2}$を示します。 $$ Q=DC_\text{2}=0.9\tag{589.2} $$ となっています。

前のブログ 次のブログ

別ページのサブツリーです。これはSM1のフォールトによるLFの項を表すORゲートです。内容は3つの確率の加算となります。

確率の和は、 $$ Q=2.176957\times10^{-9}\tag{588.1} $$ となっています。

次にORゲートの左下に接続されるANDゲートは、2nd SMであるSM2によって検出されないSM1のフォールトのLFを表す確率です。 その確率は、 $$ Q=1.45\times10^{-9}\tag{588.2} $$ となっています。

ANDゲートの左下の事象は、SM1の故障率事象です。同様にミッションタイムが自動掛け算され、 $$ Q=\lambda_\text{SM1}T_\text{lifetime}=2.9\times10^{-12}\cdot5.0\times10^{3}=1.45\times10^{-8} $$ という計算が実行されています。

ANDゲートの右下の事象は、SM2のレイテントフォールトカバレージの残余$1-DC_\text{2}$です。

$$ Q=1-DC_\text{2}=0.1=1.0\times10^{-1}より、\\ DC_\text{2}=90\% $$ と逆算されます。

前のブログ 次のブログ