不信頼度$F(t)$の近似式の誤差

故障率(5)において、故障率が定数$\lambda$である場合、信頼度$R(t)$と不信頼度$F(t)$は簡単化され、それぞれ以下の式により表されることを示しました。 \[ R(t)=e^{-\lambda t} \tag{5.2} \] \[ F(t)=1-R(t)=1-e^{-\lambda t} \tag{5.3} \]

ここで、指数関数をマクローリン展開を用いて近似式を導出してみます。不信頼度$F(t)$のマクローリン展開は \[ F(t)=1-e^{-\lambda t}=\lambda t-\frac{\lambda^2 t^2}{2}+\cdots \tag{7.1} \]

ですが、ここで、$\lambda t\ll1$という条件では2次以下の項が省略可能なほど小さいため、式(7.1)は、 \[ F(t)=1-e^{-\lambda t}\approx\lambda t,~\mbox{s.t.}~\lambda t\ll1 \tag{7.2} \]

となります。実際に故障率の違いによって、不信頼度$F(t)$が正確な値と近似式でどのくらいの誤差になるかを見てみましょう。以降は車両寿命$T_{lifetime}$は一定で100,000時間(=$10^5$時間)とします。

まず、ASIL-Dの目標値である故障率$\lambda$=10FITとします。10FITは$10^{-8}$[1/H]です。$\lambda T_{lifetime}$は$10^{-8}*10^{5}=10^{-3}$であり、車両寿命付近の誤差は0.050%とかなり良く一致しています(図7.1)。

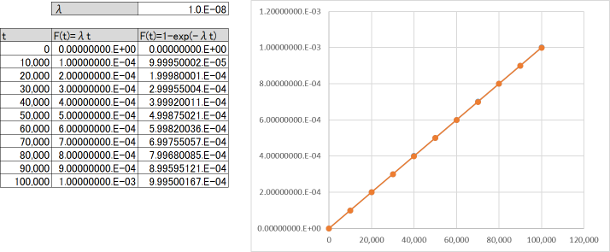
次に、ASIL-B/Cの目標値である故障率$\lambda$=100FITとします。100FITは$10^{-7}$[1/H]です。$\lambda T_{lifetime}$は$10^{-7}*10^{5}=10^{-2}$であり、車両寿命付近の誤差は0.498%と良く一致しています(図7.2)。

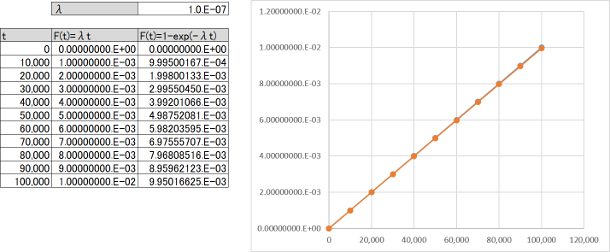
次に、故障率$\lambda$=1,000FITとします。1,000FITは$10^{-6}$[1/H]です。$\lambda T_{lifetime}$は$10^{-6}*10^{5}=0.1$であり、このあたりでは$\lambda T_{lifetime}\ll 1$とは言えなくなってくるため、誤差がだいぶ目立ってくるようになります。車両寿命付近の誤差は4.838%と無視できなくなっています(図7.3)。

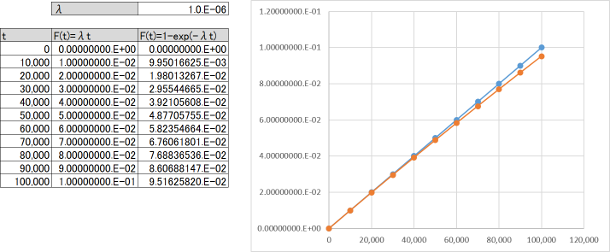
次に、故障率$\lambda$=10,000FITとします。10,000FITは$10^{-5}$[1/H]です。$\lambda T_{lifetime}$は$10^{-5}* 10^{5}=1$であり、$\lambda T_{lifetime}\approx 1$であるため、$t$が小さい時点以外は近似式は使用できません(図7.4)。

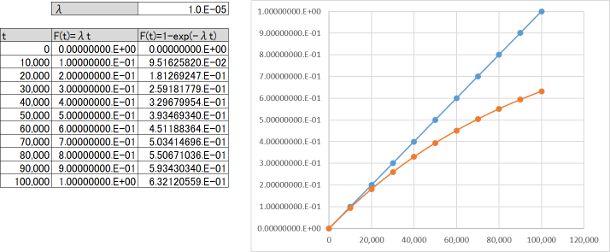
最後に、故障率$\lambda$=100,000FITとします。100,000FITは$10^{-4}$[1/H]となり、よほど$t$が小さい時点以外は近似式は使用できません(図7.5)。

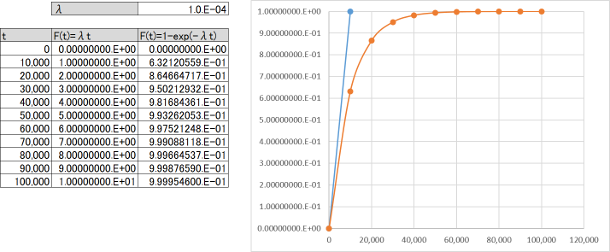
それでは故障率がどれくらいの時に誤差が5%に収まるでしょうか？前述のように1,000FITの場合は車両寿命まで誤差が5%未満だったので、上の10,000FIT及び100,000FITの場合を調べたのが図7.6です。横軸は誤差を表し、縦軸は時間$t$を表します。

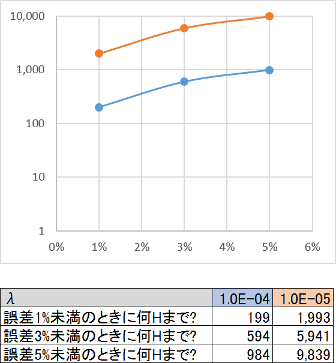
これでみると大体$\lambda t$が0.1未満のときに、車両寿命における近似値の誤差が5%未満となると思っておけばよさそうです。この誤差のことを本稿では「Exponentialの一次近似誤差」と呼ぶことにします。

エレメント単体の故障率については大方説明してきました。次回からはシステム(アイテム)の故障率の計算方法についてとなります。

前のブログ 次のブログ