|
21 |
確率コントリビューション |
弊社の考えるPMHF式について、再度DPFについて考察します。
2nd Editionから引用したシステムアーキテクチャ図を図486.1に示します。IFがVSGとなるのを抑止する(抑止確率$K_\mathrm{IF,RF}$)のと同時に、IFがレイテントとなるのを抑止する(抑止確率$K_\mathrm{IF,DPF}$)SM1が存在します。また、SM1がレイテントとなるのを抑止する(抑止確率$K_\mathrm{SM,DPF}$)SM2が存在します。
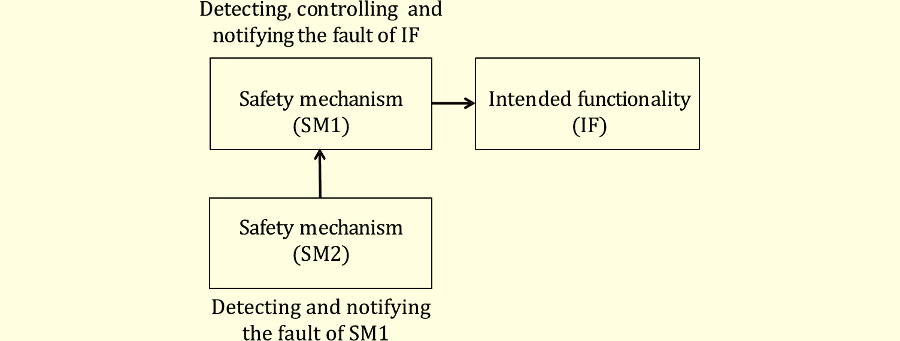
このモデルには一点問題があります。それは、冗長の場合、すなわち、IFとSM1が同機能である場合はSM2の存在が曖昧になることです。SM1の機能はIFのVSG抑止(1st SMの機能)及びLF抑止(2nd SMの機能)となっているのに対して、SM2はSM1に対するLF抑止(2nd SMの機能)です。
問題になるのはLATの場合です。これはSM1にフォールトが起きた場合に到達する状態ですが、この際に問題はIFに対する1st SMの機能喪失は当然として、2nd SM機能まで喪失するか否かです。
- 喪失する場合 --- おそらく2nd editionの想定はこのようですが、この場合はLATに来た時刻により、LATの状態確率が変わってくるため、マルコフ性が成立しません。マルコフ性が成立しない場合の確率積分は非常に難しくなり解けないと言われています。
- 喪失しない場合 --- LATの状態確率は来た時刻に依存しないため、マルコフ性が成立します。
そもそも1st SMと2nd SMが別エレメントと考えると2nd SMは故障しないという定理から、2番目が良いと考えられます。
なお、本稿はRAMS 2023に投稿中のため一部を秘匿していますが、論文公開後の2023年2月頃に開示予定です。RAMS 2023が終了したため、秘匿部分を開示します。

Leave a Comment