OPR⇒SPFの平均PUDの計算

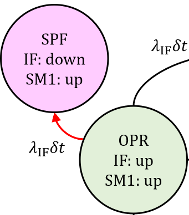
まずOPRステートからSPFステートへの、$t$から$t+dt$までの微小遷移確率を0から$T_\text{lifetime}$まで積分したものの時間平均、つまり平均PUDを計算します。時刻$t$でOPRにおいてはIF=upであったのに対し、時刻$t+dt$までの間にIFにフォールトが起き、IF=downとなると同時にSPFに移行します。平均PUDの定義については平均PUD定義式(66.13)をご覧ください。

SM1のVSG prevent能力はアーキテクチャ的に決定されるため、他の事象とは独立と考えます。 CTMCの平均PUD基本式(101.5)について、条件付き確率の公式を用いて、 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF,IFU}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{OPR\ at\ }t\cap\mathrm{IF\ down\ in\ }(t, t+dt]\cap\overline{\mathrm{VSG\ of\ IF\ preventable}}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{OPR\ at\ }t\}\Pr\{\overline{\mathrm{VSG\ of\ IF\ preventable}}\} \end{eqnarray} \tag{103.1} $$ ここで、OPRはIF、SM1共にupであるから、 $$ \Pr\{\mathrm{OPR\ at\ }t\}=\Pr\{\mathrm{IF\ up\ at\ }t\cap\mathrm{SM\ up\ at\ }t\} \tag{103.2} $$ IFとSM1の稼働状態は独立事象で、IFはアンリペアラブル、SM1がリペアラブルです。ここでIFがアンリペアラブルなことを特に$\mathrm{IF^U}$と表します。SM1は常にリペアラブルなのでそのままです。すると、(103.2)は $$ \Pr\{\mathrm{OPR\ at\ }t\}=\Pr\{\mathrm{IF^U\ up\ at\ }t\}\Pr\{\mathrm{SM\ up\ at\ }t\}\\ =R_\mathrm{IF}(t)A_\mathrm{SM}(t)\tag{103.3} $$ と書けます。ここで、以下の条件付き確率において、CがAともBとも独立であるとき、次の独立条件付き確率式 $$ \require{cancel} \Pr\{\mathrm{A}\ |\ \mathrm{B}\cap\mathrm{C}\}=\frac{\Pr\{\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\}}{\Pr\{\mathrm{B}\cap\mathrm{C}\}}=\frac{\Pr\{\mathrm{A}\cap\mathrm{B}\}\cdot\bcancel{\Pr\{\mathrm{C}\}}}{\Pr\{\mathrm{B}\}\cdot\bcancel{\Pr\{\mathrm{C}\}}}=\Pr\{\mathrm{A}\ |\ \mathrm{B}\}\tag{103.4} $$ が成り立つため、(103.1)の右辺積分中の条件付き確率式に(103.2)、(103.4)、及び微小故障条件付き確率式(66.8)を用いれば、IFはアンリペアラブルであるため、 $$ \Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR\ at\ }t\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\cap\bcancel{\text{SM up at }t}\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}=\lambda_{\mathrm{IF}}dt \tag{103.5} $$ よって、(103.1)に(103.5)、(103.3)、$\Pr\{\overline{\mathrm{VSG\ of\ IF\ preventable}}\}=1-K_{\mathrm{IF,RF}}$(100.3)を用いた上で、故障率(66.6)及びPUA(59.8)を適用すれば、平均PUDは、 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF,IFU}}}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_{\mathrm{IF,RF}})R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_{\mathrm{IF}}dt\\ &=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[1-Q_\text{SM}(t)\right]f_{\mathrm{IF}}(t)dt\\ &=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_{\mathrm{IF}}(t)dt-\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\text{SM}(t)f_{\mathrm{IF}}(t)dt\\ &=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}F_\text{IF}(T_\text{lifetime})\\ & &-\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_\text{SM,MPF})F_\text{SM}(t)+K_\text{SM,MPF}F_\text{SM}(u)\right]f_{\mathrm{IF}}(t)dt,\\ & &\text{ただし、}u:=t\bmod\tau \end{eqnarray} \tag{103.6} $$ よって、$1-e^{-\lambda_{\mathrm{IF}}t}\approx\lambda_{\mathrm{IF}}t$と近似するMaclaurin展開及び弊社積分公式により、 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF,IFU}}}&\approx&(1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}-\frac{1-K_{\mathrm{IF,RF}}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ &=&(1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}-(1-K_{\mathrm{IF,RF}})\alpha\\ & &\text{ただし、} \alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau] \end{eqnarray} \tag{103.7} $$

RAMS 2020においてPMHF式の論文発表が終了したため、本記事を開示します。

前のブログ 次のブログ