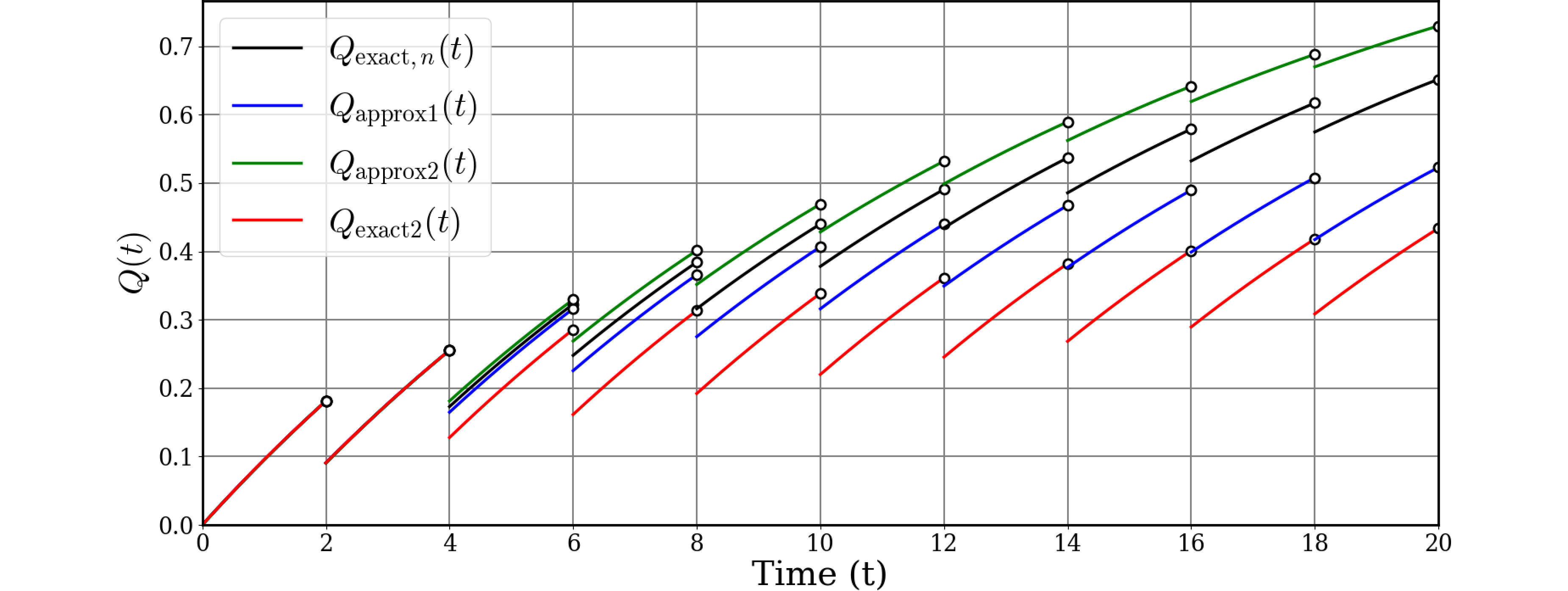
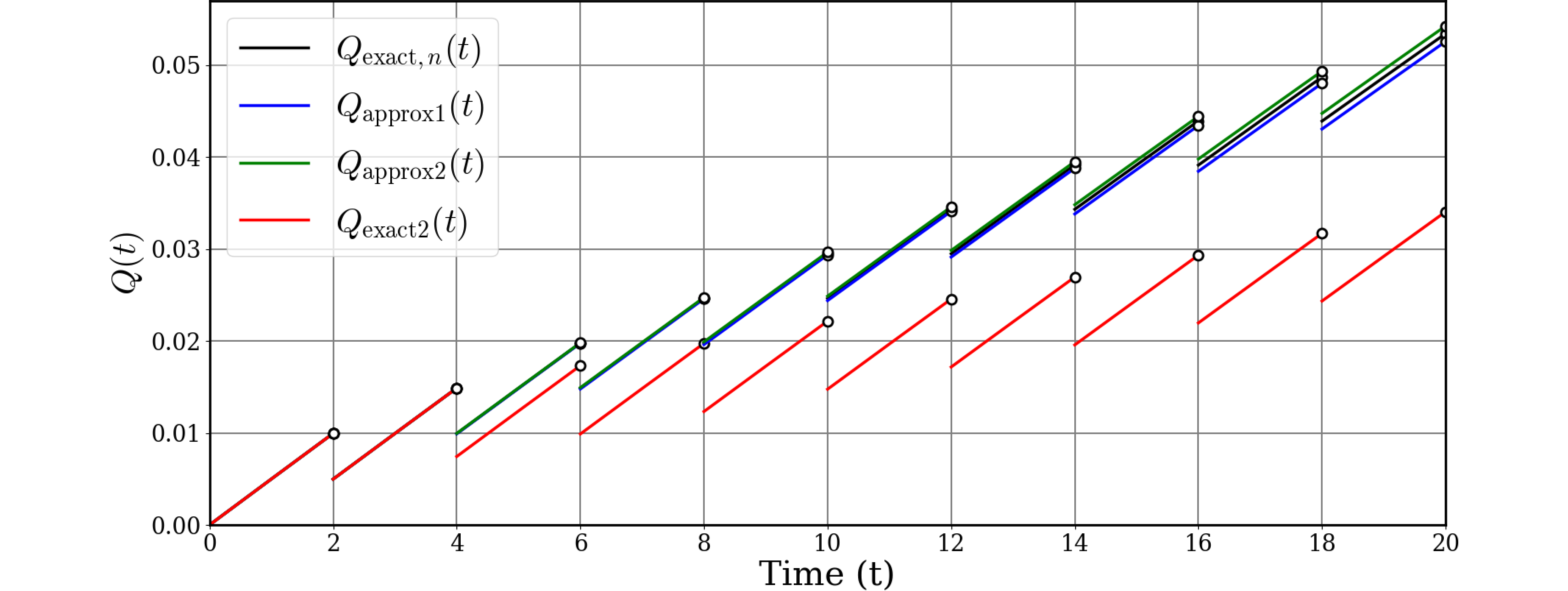
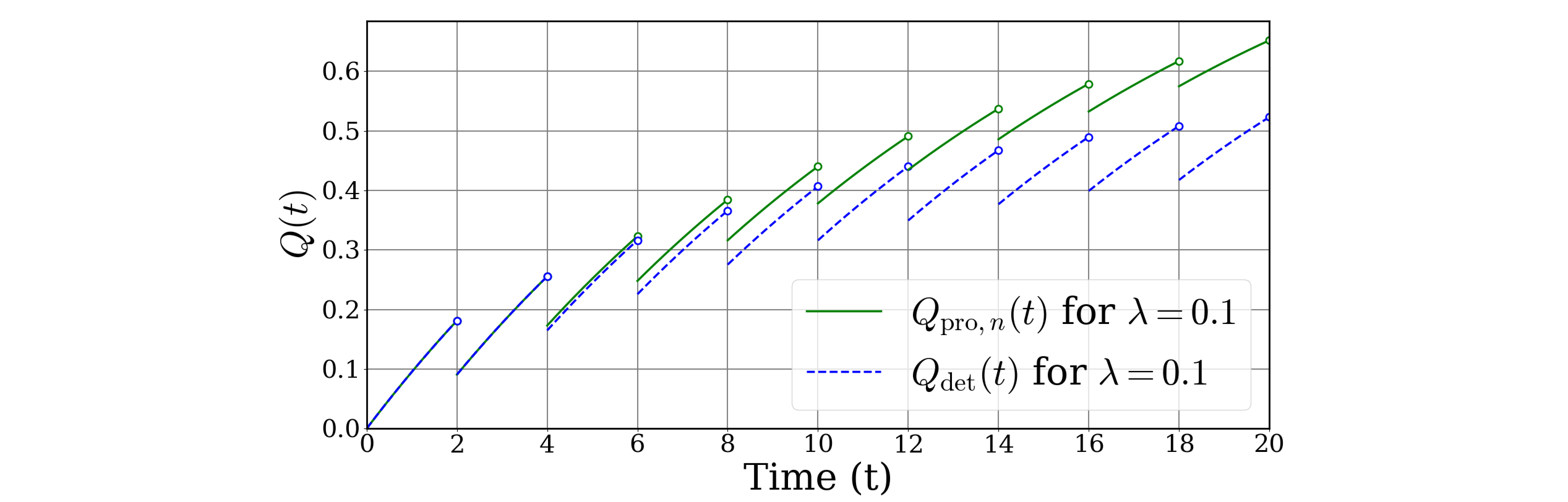
ChatGPTにグラフを3本書いて貰います。区間差分をどのように取るかの違いで3種類考えられます。PIRの原則ではこの区間差分(検査区間内の累積分布)の$K_\text{MPF}$倍が修理度となります。
- 区間内の累積分布=区間不稼働度の差分: $Q_\text{exact}(t)$においては$Q(i\tau)-Q((i-1)\tau)$
- 区間内の累積分布=区間不信頼度が一定: $Q_\text{approx1}(t)$においては$-F(\tau)$
- 区間内の累積分布=区間不信頼度の差分: $Q_\text{approx2}(t)$においては$F(i\tau)-F((i-1)\tau)$
$\dagger Q_\text{approx2}(t)$において区間不信頼度($K_\text{MPF}$倍する前の修理度)は、
$$
\require{cancel}
F(i\tau)-F((i-1)\tau)=\bcancel{1}-e^{-i\tau}-\bcancel{1}+e^{-(i-1)\tau}\\
=e^{-i\tau}\left(e^{\tau}-1\right)=-F(\tau)e^{-i\tau}=-F(\tau)R(i\tau)
$$
修理度の絶対値が$R(i\tau)$だけ次第に小さくなりますが、それを無視し$R(i\tau)\approx1$とすれば$Q_\text{approx1}(t)$と同じになります。
import numpy as np
import matplotlib.pyplot as plt
from functools import lru_cache
plt.rcParams['font.family'] = 'serif'
plt.rcParams['mathtext.rm'] = 'Times New Roman'
plt.rcParams['mathtext.fontset'] = 'cm'
# パラメータ設定
lambdaVal = 0.1 # 故障率
tau = 2 # 点検期間
K = 0.5 # 修復率
epsilon = 0.00001 # 不連続点の直前を示すために使用する小さい値
# 関数定義
def R(t):
"""信頼度関数"""
return np.exp(-lambdaVal * t)
def F(t):
"""故障関数"""
return 1 - R(t)
@lru_cache(maxsize=None)
def Q_n(t, n):
"""Q_nの再帰関数。結果をキャッシュする。"""
if n == 0:
return F(t)
else:
tau_n = n * tau
tau_n_minus_1 = (n - 1) * tau
return
def Q_approx1(t):
"""tにおけるQ(t)の近似値を計算する関数"""
u = t % tau
return (1 - K) * F(t) + K * F(u)
# 定義された Q_approx2(t) を追加して描画します。
def Q_approx2(t, n):
"""tにおけるQ_approx2の近似値を計算する関数"""
return F(t) - n * K * (F(t) - F(t - tau))
# グラフ描画
fontsize_axes_label = 24 * 1.2
fontsize_ticks = 16 * 1.2
fontsize_legend = 24 * 1.2
# グラフ描画
plt.figure(figsize=(18, 11))
# 軸(spines)の線幅を太くする
ax = plt.gca() # 現在の軸を取得
spine_width = 2 # 軸の線幅
for spine in ax.spines.values():
spine.set_linewidth(spine_width)
# 凡例用のダミープロット
plt.plot([], [], '-', label=r'$Q_{\mathrm{exact},n}(t)$ for $\lambda = 0.1$', color='black')
plt.plot([], [], '-', label=r'$Q_{\mathrm{approx1}}(t)$ for $\lambda = 0.1$', color='blue')
plt.plot([], [], '-', label=r'$Q_{\mathrm{approx2}}(t)$ for $\lambda = 0.1$', color='green')
# 不連続性を示すために各区間を個別にプロット
for i in range(10):
start = i * tau
end = (i + 1) * tau - epsilon
t_vals = np.linspace(start, end, 200)
Q_exact_vals = [Q_n(t, i) for t in t_vals[:-1]] # 区間の最後の点を除外してプロット
Q_approx1_vals = [Q_approx1(t) for t in t_vals[:-1]]
Q_approx2_vals = [Q_approx2(t, i) for t in t_vals[:-1]]
plt.plot(t_vals[:-1], Q_exact_vals, 'k-', lw=2.5)
plt.plot(t_vals[:-1], Q_approx1_vals, 'b-', lw=2.5)
plt.plot(t_vals[:-1], Q_approx2_vals, 'g-', lw=2.5)
# 区間の終わりに白丸をプロット
plt.plot(end, Q_n(end, i), 'o', mfc='white', mec='black', mew=2, markersize=8)
plt.plot(end, Q_approx1(end), 'o', mfc='white', mec='black', mew=2, markersize=8)
plt.plot(end, Q_approx2(end, i), 'o', mfc='white', mec='black', mew=2, markersize=8)
plt.xlabel('Time (t)', fontsize=fontsize_axes_label)
plt.ylabel(r'$Q(t)$', fontsize=fontsize_axes_label)
plt.xticks(np.arange(0, 11 * tau, tau), fontsize=fontsize_ticks)
plt.yticks(fontsize=fontsize_ticks)
legend = plt.legend(fontsize=fontsize_legend)
for handle in legend.legendHandles:
handle.set_linewidth(2.5) # ここで線の太さを指定
plt.grid(True, color='gray', linestyle='-', linewidth=1.4)
plt.ylim(bottom=0)
plt.xlim(0, 10 * tau)
plt.subplots_adjust(left=0.14, bottom=0.14)
plt.show()
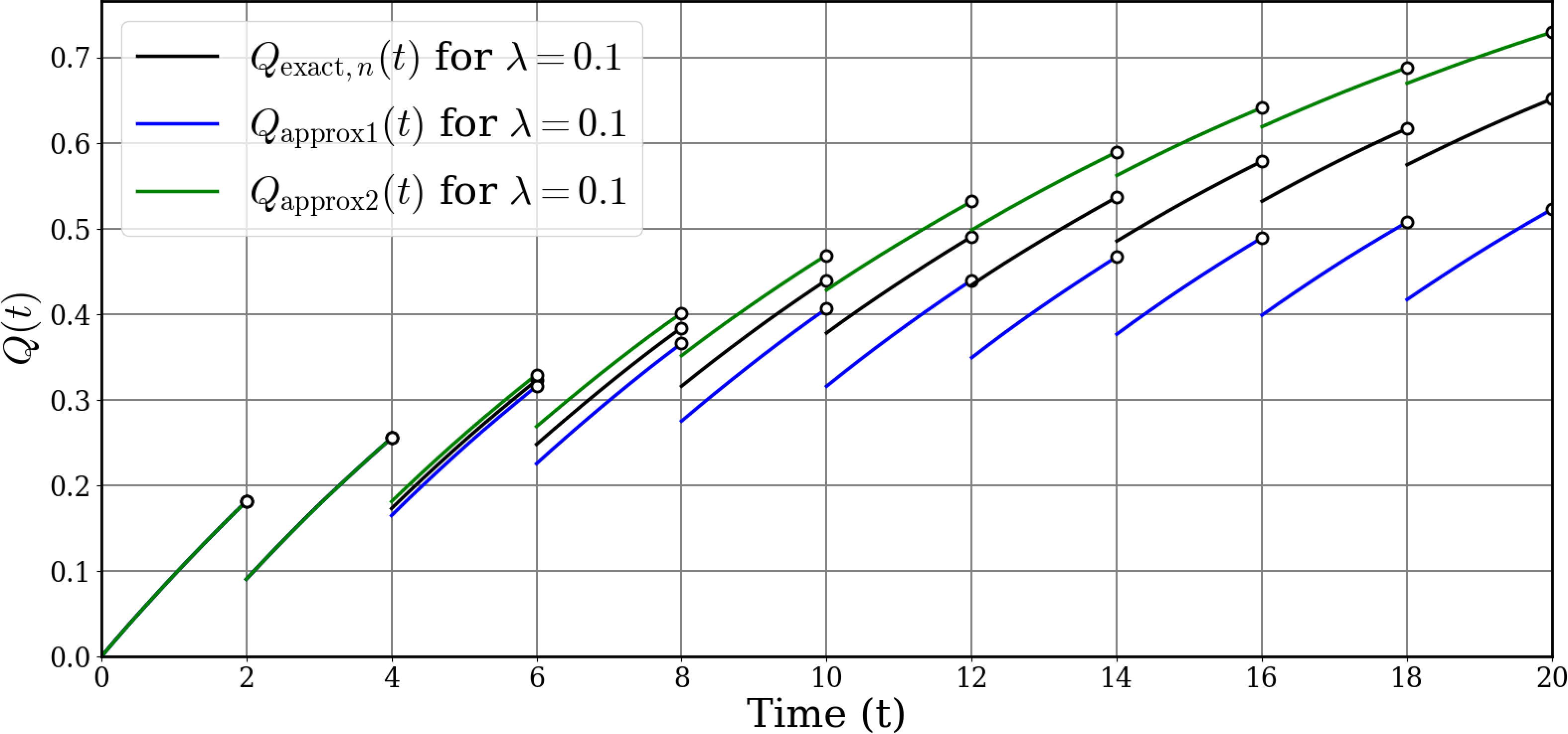 図877.1 3つのグラフ
図877.1 3つのグラフ
このように、$Q_\text{exact}(t)$が最も正確な不稼働度(PUA)であり、上記$\dagger$のように修理度を大と近似すると$Q_\text{approx1}(t)$で下界となり、修理度を小と近似すると$Q_\text{approx2,n}(t)$で上界となることが分かります。
なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。
 前のブログ
次のブログ
前のブログ
次のブログ