PUA関連論文シリーズ最後は以下の論文です。

P. Hokstad, “The Failure Intensity Process and the Formulation of Reliability and Maintenance Models,” Rel. Eng. Syst. Safety, vol. 58, no. 1, pp 69–82, (Oct.) 1997.

以降翻訳はDeepLによるものです。まずアブストラクトを示します。

故障事象モデルの定式化に対する統一的なアプローチを示す。これは、修理可能なものと修理不可能なもの、予防保全と是正保全の両方を分析するための共通の枠組みを提供するものであり、休止故障のあるものにも適用できる。提案された手順は、一連のグラフによってサポートされ、それによって、固有の信頼性（すなわち、ハザード率）と保守・修理方針の両方の重要性を明らかにする。様々な故障強度の概念の定義／解釈は、このアプローチの基本である。したがって、これらの強度間の相互関係を検討し、それによってこれらの概念の明確化にも貢献する。これらの概念の中で最も基本的なものである故障強度過程は、計数過程（マーチンゲール）で使用されるものであり、その時点までの品目の履歴が与えられた時点tにおける故障率である。提案するアプローチは、いくつかの標準的な信頼性とメンテナンスのモデルを考えることによって説明される。

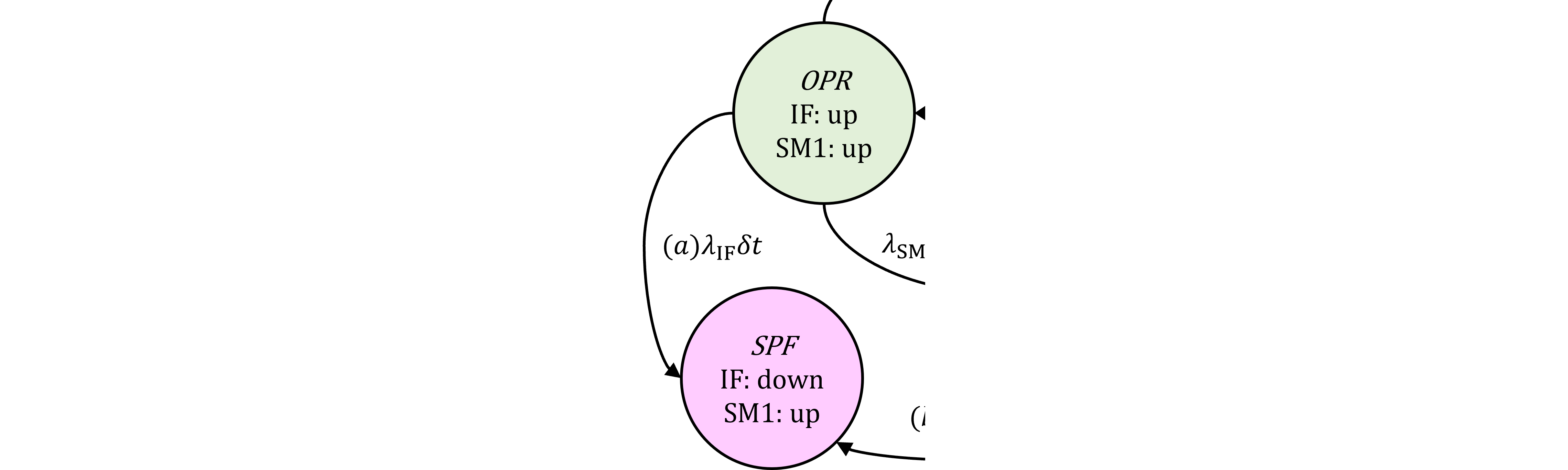
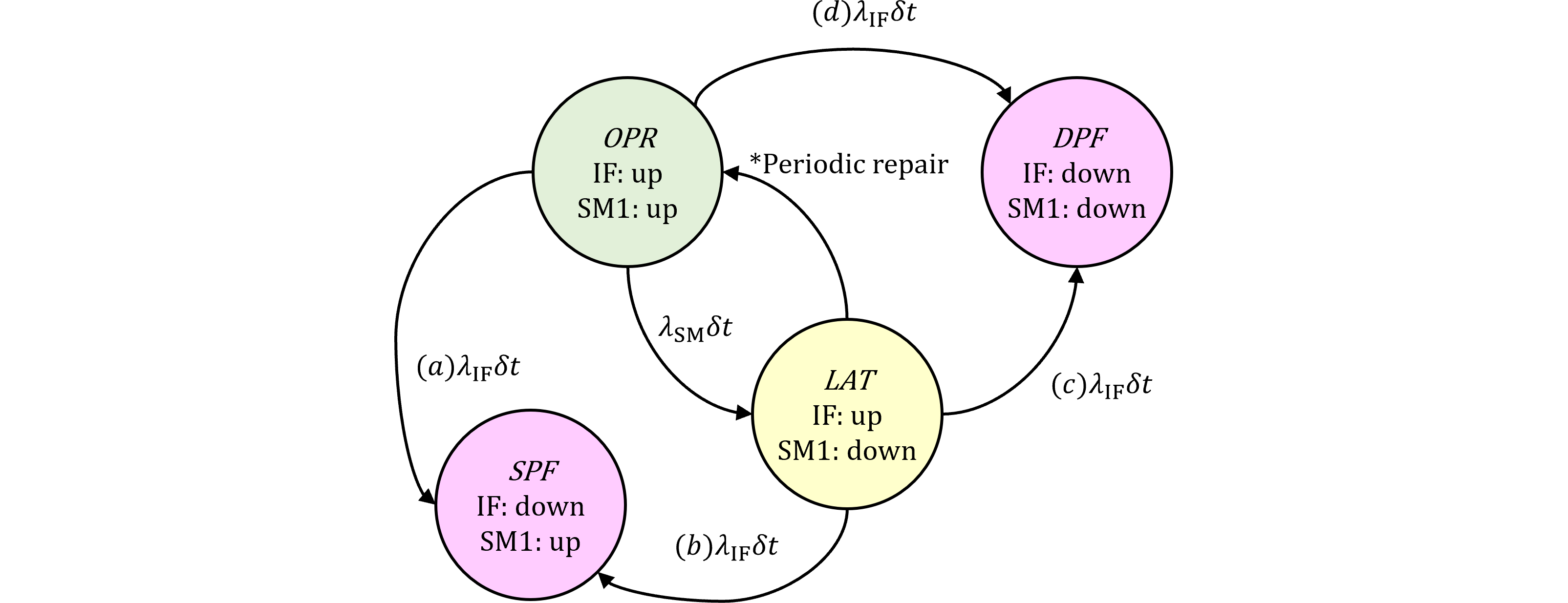
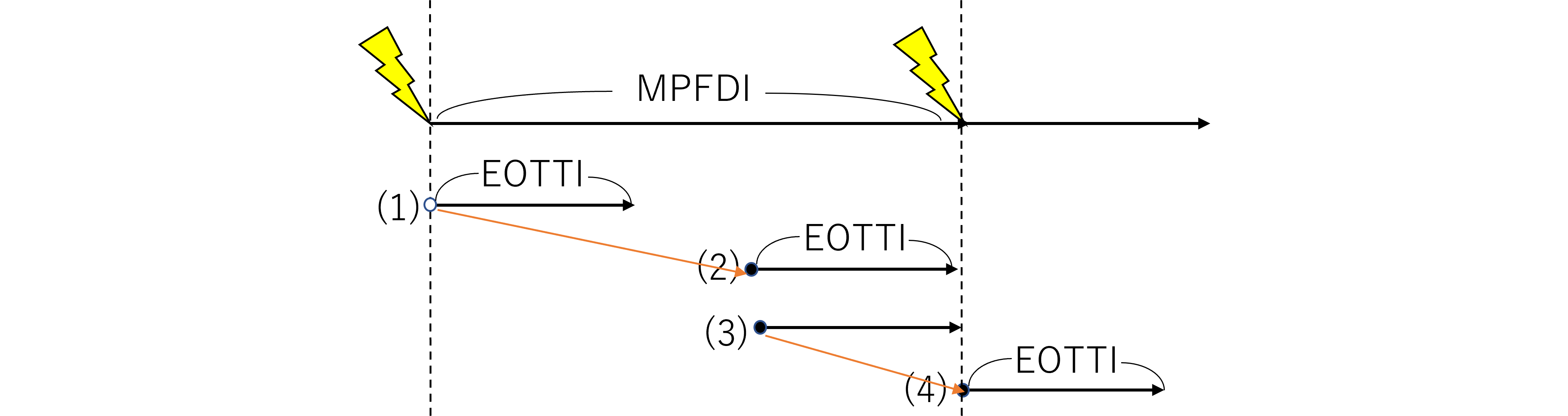
いろいろな不稼働度モデルが紹介されていますが、我々の関心があるのは定期検査を持つModel Dと呼ばれるモデルです。

Model D (休眠故障と定期的なテストを伴うアイテム)

一方、著者によれば、様々な確率過程は以下の定義となります。

Average intensity、もしくはAROCOF (Average Rate of OCcurrence Of Failure)は、 $$ i_\tau=\frac{1}{\tau}\int_0^\tau I(t)dt=\frac{1}{\tau}M(\tau) $$ 我々の定義では、$I(t)$は$q(t)$と、$M(t)$は$Q(t)$と定義します。元になる非修理系において一般的な記法であるPDF=$f(t)$、その積分であるCDF=$F(t)$を踏襲するなら$i$や$I$の大文字小文字は逆にして欲しかったところです。

我々は特に車両寿命間の平均PUDが知りたいため、PFHも同様の定義ですが、 $$ M_\text{PMHF}=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}} q(t)dt=\frac{1}{T_\text{lifetime}}Q(T_\text{lifetime})=i_{T_\text{lifetime}} $$ が求めたい平均不稼働密度です。

前のブログ 次のブログ

次は以下の論文です。

J. Sobral, L. Ferreira, “Availability of Fire Pumping Systems Under Periodic Inspection,” J. Build. Eng., vol. 8, pp 285–291, (Dec.) 2016.

以降翻訳はDeepLによるものです。まずアブストラクトを示します。

消防ポンプシステムは、住宅、商業施設、工業施設など、あらゆる建物の消火に使用されている。これらのシステムは、建物保護の目的で設置された手動または自動装置に必要な水流と圧力を供給する役割を担っている。従って、望ましくない火災が発生した場合に、その可用性を保証することは非常に重要である。本稿では、消防ポンプ設備が定期的な点検や試験を受けた場合の可用性に焦点を当てる。これらの検査や試験は、システムの挙動を観察し、コンポーネントやサブシステムの潜在的な隠れた故障を検出するために実施される。本論文で提案する方法論は、第一段階として、重要な機器の要求時に故障が発生する確率を分析し、この重要な段階の成功確率を分析することに焦点を当てている。また、消防ポンプシステムの望ましい可用性に対する点検・試験頻度の影響も示す。

適用分野はだいぶ異なりますが、論文の(2)式は瞬間不稼働度を求めるもので、

$$ Q(T)=\frac{1}{T}\int_0^Tq(t)dt $$ と書かれています。これは我々のPUAと同じで、その場合$q(t)$はPUDということになります。

以降では本論文がPMHFをどのように導出するかを見ていきます。

$$ Q(\tau)=\frac{1}{\tau}\int_0^\tau(\tau-t)f(t)dt=\frac{1}{\tau}\int_0^\tau F(t)dt $$ ここで、F(t)を導出しており、$\tau-t$はダウンタイム幅と解釈されますが、式が誤っているようです。本来$f(t)$を積分すると$F(t)$になるため、積分せずに$F(t)$となることは改善の余地がありそうです。ただしavailabilityとしてsawtooth波形を掲載しているのは正しいので、その後の議論がおかしくなっているようです。

式はこの程度しか掲載されておらず、著者はPUAの一般式を導出していません。従ってこの論文の分析はここまでです。

前のブログ 次のブログ

PUAに関する論文が複数出ているので、その内容を確認します。

J. Famfulik, M. Richtar et al, "Application of hardware reliability calculation procedures according to ISO 26262 standard," Qual. Rel. Eng. Int. 2020, pp. 1-15, doi: 10.1002/qre.2625

以降翻訳はDeepLによるものです。まずアブストラクトを示します。

自動車産業における機能安全評価のための規格ISO 26262（2018年版）第2版では、ランダムハードウェア故障の確率的メトリック（PMHF）を使用したハードウェア評価が要求されている。この規格では、フォールトツリー解析（FTA）の活用を強く推奨しているが、具体的な計算例は示されていない。そこで、本稿では、電子システムのさまざまなハードウェア・アーキテクチャに対する数式の導出と説明を含む計算手順について説明する。記述されている数式は、多重故障の影響やelf-testの影響を考慮しているが、数式は比較的単純である。この単純さにより、ハードウェア設計の頻繁な変更が予想されるハードウェア開発の初期段階で使用することができる。したがって、ケーススタディを添付したこの論文は、科学者だけでなく、自動車産業における重要な安全関連電子システムの開発者を対象としている。

PMHFの数学的な定義を平均的な車両寿命間の不信頼度の時間平均とした論文の(3)式は

$$ P_\text{MHF}=\frac{F_\text{AVG}}{t} $$ と書かれています。改善点としては細かいことを言えば、PMHFの表記は規格Part 10に従えば$P_\text{MHF}$ではなく$M_\text{PMHF}$です。またPMHFは車両寿命間の時間平均故障確率であるため、分母は$t$ではなく、$T_\text{lifetime}$(論文中では大文字の$T$)です。

従って論文の(3)式は正しくは $$ M_\text{PMHF}=\frac{F_\text{AVG}}{T} $$

とすべきです。ここで問題は$F_\text{AVG}$は不信頼度の平均です。ところがこれはおかしく、$T$で割っていることが車両寿命間の時間平均を表すので、分子は積分値であるべきです。そのため筆者の平均値の認識には改善点があると言うべきです。これは以下の式にも認めることができます。論文の(5)式は

$$ F(t)=\lambda t $$ これは不信頼度の式で、非修理系においては正しい式です。ところが問題は次の$F_\text{AVG}$で、論文の(6)式は

$$ F_\text{AVG}=\frac{1}{t}\int_0^t F(t)dt $$ つまり、(6)式においてF(t)を平均化した後さらに(3)式において$T$で割るという2重に平均を取ることを行っています。

本来は、我々の記法に従えば、 $$ M_\text{PMHF}=Q_\text{AVG}=\frac{Q(T)}{T} =\frac{1}{T}\int_0^T q(t)dt $$ とするのが正しい方法です。ここで$Q(t)$はPUA, $q(t)$はPUDです。

以降では本論文がPMHFをどのように導出するかを見ていきます。

前のブログ 次のブログ

次は(15)の導出です。

論文"Generic Equations for a Probabilistic Metric for Random Hardware Failures According to ISO 26262"において、以下の2か所の式変形過程が分からないが、どうして次の式(13), (15)が導出されるのか？

(13)　省略、前ページで解説

これは既に過去ブログでも記載済みなのでその箇所を返信しました。

Equation (103.6) in the following blog post is what you are looking for.
次のブログ記事の式(103.6)があなたが探しているものです。
https://fs-micro.com/post/show/id/103.html
Here's the trick: we transform it using $F(t)$ instead of $R(t)$. Because our integral formula
ここにトリックがあります。$R(t)$の代わりに$F(t)$を用います。なぜなら、我々の積分公式
https://fs-micro.com/post/show/id/60
can be used.
が使えるからです。

返信の際に$F(t)$に言及したのは、読者の方がご自分で変形し、$R(t)$の形式を導出した後行き詰っていたのでヒントを示しています。以下に記事の(103.6)を再掲します。

よって、(103.1)に(103.1.5)、(103.1.3)、$\Pr\{\overline{\text{VSG of IF preventable}}\}=1-K_\text{IF,RF}$(100.3)を用いた上で、故障率(66.6)及びPUA(59.8)を適用すれば、平均PUDは、 $$ \begin{eqnarray} \overline{q_\text{SPF,IFU}}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\text{IF,RF})R_\text{IF}(t)A_\text{SM}(t)\lambda_\text{IF}dt\\ &=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[1-Q_\text{SM}(t)\right]f_\text{IF}(t)dt\\ &=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_\text{IF}(t)dt-\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\text{SM}(t)f_\text{IF}(t)dt\\ &=&\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}F_\text{IF}(T_\text{lifetime})\\ & &-\frac{1-K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_\text{SM,MPF})F_\text{SM}(t)+K_\text{SM,MPF}F_\text{SM}(u)\right]f_\text{IF}(t)dt,\\ & &\text{ただし、}u:=t\bmod\tau \tag{103.1.6} \end{eqnarray} $$ よって、$F_\text{IF}(t)=1-e^{-\lambda_\text{IF}t}\approx\lambda_\text{IF}t$と近似する0におけるTaylor展開(すなわちMaclaurin展開)及び弊社積分公式により、 $$ \overline{q_\text{SPF,IFU}}\approx(1-K_\text{IF,RF})\lambda_\text{IF}-\frac{1-K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}\tau\right]\\ \tag{103.1.7} $$

1st editionでは定期修理期間を$\tau$で表していましたが、2nd editionでは表記が$T_\text{service}$に変わりました。従って、 $$ \overline{q_\text{SPF,IFU}}\approx(1-K_\text{IF,RF})\lambda_\text{IF}-\frac{1}{2}(1-K_\text{IF,RF})\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}T_\text{service}\right] $$ となり、(15)が成立します。

前のブログ 次のブログ

本ブログでは5年ほど前に初出の記事を掲載した後この記事から5本に渡り$Q(t)$について記載しました。

中でも初出の記事は計算過程を示しています。ここでは(59.5)から(59.6)への導出には説明がなかったのでここで解説します。再掲すれば、(626.1)から(626.4)への導出です。まずA(t)は、

$$ A(t):=R(t)+\int_0^t m(x)R(t-x)dx\tag{626.1} $$

ここで$m(x)$はリニューアル密度と呼ばれますが、その時間積分した$M(x)$は時刻$x$までに故障した分について検査・修理した分であり、2つの要素が掛けられています。つまり検査率を$K_\text{SM,MPF}$(const.)、故障した分を$F_\text{SM}(x)$としたとき、検査・修理は連続時間ではなく定期的、すなわち離散的に実行されるため、修理時刻$x$は、$x=i\tau,\ i=1, 2, 3,...$という飛び飛びの値をとります。

故障した時刻に無関係に修理は行われます。これは故障する確率に関わらず、検査・修理時には検査可能な故障は全て修理されるためです。ということは前回の修理時には検査可能な故障＝不信頼度はゼロになるはずで、検査周期＝$\tau$においては不信頼度は$F_\text{SM}(\tau)$(const.)となります。よって、$M(x)$は $$ M(i\tau)=\int_0^\tau m(x)dx=K_\text{SM,MPF}\int_0^\tau f(x)dx=K_\text{SM,MPF}F_\text{SM}(\tau),\ \ i=1, 2, ...\tag{626.2} $$ のようにconst.となります。そして、離散的な関数の積分はシグマに置き換えられるため、 $$ \int_0^t m(x)R(t-x)dx=K_\text{SM,MPF}F_\text{SM}(\tau)\sum_{i=1}^{n}R(t-i\tau) \tag{626.3} $$ となります。これらを(626.1)に代入すれば、

$$ A_\text{SM}(t)=R_\text{SM}(t)+K_\text{SM,MPF}F_\text{SM}(\tau)\sum_{i=1}^{n}R_\text{SM}(t-i\tau)\tag{626.4} $$ が得られます。$Q(t)$に書き換えれば、 $$ Q_\text{SM}(t)=F_\text{SM}(t)-K_\text{SM,MPF}F_\text{SM}(\tau)\sum_{i=1}^{n}R_\text{SM}(t-i\tau)\\ =\img[-1.35em]{/images/withinseminar.png},\ \ s.t.\ \ u\equiv t-n\tau=t-\lfloor\frac{t}{\tau}\rfloor\tau \tag{626.5} $$ が得られます。さらにこれを時間$t$微分したものが弊社命名のPUD(Point Unavailability Density)であり

$$ q(t)=\img[-1.35em]{/images/withinseminar.png} $$ となり、この車両寿命間の時間平均こそがPMHFとなるわけです。 $$ M_\text{PMHF}\equiv\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}q(t)dt=\frac{1}{T_\text{lifetime}}Q(T_\text{lifetime}) $$ なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。

前のブログ 次のブログ

PMHFの導出の前提には2通りあります。具体的には、1st SMによって検出され、VSG抑止されたフォールト(MPF detected fault)に関して、

• MPF detected faultをlatent faultとする
• MPF detected faultを直ちに修理する

の2通りの立場があります。規格にはMPF detected faultの処置について明確に書かれていないので、従来はLFとするとしていました。この前提に基づき2020 RAMS論文を投稿しています。

ところが、これだとLFMの定義と矛盾するので、その矛盾の解消のため、2番目の立場を採用した2022 RAMS論文(IEEE未収録)を投稿しました。

後者のまとめの記事は記事#374に書きましたが、前者をまとめていませんでしたので、以下に表を用いてまとめます。元になる表と導出法は、それぞれ表375.1及び表368.2と記事#376です。

$$ \text{ただし、} \begin{cases} \alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ \beta:=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \end{cases}\\ \begin{cases} \begin{eqnarray} 非冗長系の時は\color{red}{K_\text{IF,det}}&=&1\\ 冗長系の時は\color{red}{K_\text{IF,det}}&=&0, K_\text{IF,RF}=1\\ \end{eqnarray} \end{cases} $$

表492.1に対して、非冗長系、冗長系のKパラメータを上記に示すとおり代入した表を表492.2及び表492.3に示します。

非冗長系

$$ M_\text{PMHF,NRD}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+2K_{\text{IF,RF}}\alpha}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau] \tag{492.1}$$

(492.1)に関しては後者の記事、#374との違いは係数2の違いとなります。

冗長系

$$M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}=\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\tag{492.2}$$

(492.2)に関しては後者の記事、#374との違いはありません。その理由は、冗長系においてはMPF detected faultが存在しないためです。

$\dagger$規格式1: 規格第1版 Part 10-8.3.3の第1式の条件。ブログの図367.1)において、IFが後にフォールトする場合=(a)SPF、(b)SPF及び(c)DPF。(d)DPFはSMが後にフォールトする場合なので対象外
$\dagger$規格式3: 規格第1版 Part 10-8.3.3の第3式の条件。ブログの図367.1)において、IF, SMのフォールトの順を問わない場合=(a)SPF、(b)SPF、(c)DPF及び(d)DPF。

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ

OPR⇒SPFの平均PUDの計算

従来はMPF detectedはnon faultyでしたが、今回EOTTIの導入に伴い、SM1の時間制約としてのEOTTI後に、VSG抑止の時間切れとなることからSPFとするように変更しました。従って、MPF detectedといえどもSPF計算に関係してきます。 前稿#369を参照し、OPRからSPFへの平均PUD(66.13)を計算します。

OPRからSPFへの平均PUDは、 $$ \overline{q_{\mathrm{SPF(a),IFU}}}=\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF\ via\ (a)\ at\ }T_\text{lifetime}\}\tag{384.1} $$ ここで、表368.1より、IF non preventableのupは(2)及び(4)のうちEOTTIでカバーされない分=miss分=(383.1)、の2排他条件であるため、 $$ \begin{eqnarray} (384.1)&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\left(\mathrm{OPR_\overline{prev}\ at\ }t\cup\mathrm{OPR_\text{prev}\ at\ }t\cap miss\right)\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ & &+\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\left(\mathrm{OPR_\overline{prev}\ at\ }t\cap miss\right)\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\overline{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\}\\ & &+\frac{\Pr\{miss\}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\text{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\text{prev}\ at\ }t\}\\ \end{eqnarray} \tag{384.2} $$ 前稿#369の(369.5)より、 $$ \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\overline{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\mathrm{IF,RF})R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.3} $$ さらに、 $$ \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_{prev}\ at\ }t\}\Pr\{\mathrm{OPR_{prev}\ at\ }t\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}K_\mathrm{IF,RF}R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.4} $$ は明らかであるから、これらを(384.2)に代入して、 $$ \require{cancel} (384.2)=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-\bcancel{K_\text{IF,RF}})+K_\text{IF,RF}\left(\bcancel{1}-\frac{T_\text{eotti}}{T_\text{mpfdi}}\right)\right]R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\text{IF,RF}\right)R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.5} $$ よって、(103.6)の結果を用い、$\tau=T_\text{mpfdi}$であるから、 $$ \begin{eqnarray} (384.5)&\approx&\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\right)\lambda_\mathrm{IF}-\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\right)\alpha\\ &=&\img[-1.35em]{/images/withinseminar.png}\\ & &\text{ただし、} \alpha:=\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}\left[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}T_\text{mpfdi}\right] \end{eqnarray} \tag{384.6} $$

MPFDIに対してEOTTI分だけSM1のカバレージが減少すると解釈すると、SM1のEOTTIの制約に対して理屈に合っています。

なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。

前のブログ 次のブログ

EOTTIの問題点2点

以下は、$T_\text{mpfdi}\gt T_\text{eotti}$の場合に限ります。反対に、$T_\text{mpfdi}\le T_\text{eotti}$の場合は必ずEOTTI中に検査・修理が含まれるためSPFとなることはないので、MPF detectedは過去記事のようにup状態となります。

1. PMHF式の修正が必要
   SM1にVSG抑止の制約時間であるEOTTIが存在する場合は、CTMCの遷移条件が異なってきます。それにより、結果として得られるPMHF方程式が変わってきます。
   
   CTMC遷移条件が変更⇒平均PUD微分方程式が変更⇒結果PMHF方程式が変更
   

   図383.1　CTMC
   図383.1において、IFにフォールトが発生し、かつSM1によりそのフォールトが検出された場合、かつEOTTIが車両寿命以上の場合はVSGが抑止されている期間内に修理されることが前提のため、VSGとはなりません。一方EOTTIが車両寿命未満の場合はVSG抑止がされなくなるため、SPFとなります。つまりSM1によるMPF detectedフォールトについては、カバー範囲においても(a)の遷移が発生します。
   
   

2. MPFDIとEOTTIの性質の違い
   過去記事のように、MPFDIとEOTTIは相反する時間制約であることから、相互に入れ替えることはできません。
   
   図383.2に$T_\text{mpfdi}\gt T_\text{eotti}$の場合のMPFDIとEOTTIの関係を示します。MPFDIの周期は検出・修理周期です。これを固定し、EOTTIをずらして行くと、(1)~(2)まではEOTTI中に検出・修理は入らないため、この期間はミス期間(長さ=MPFDI-EOTTI)となります。一方、(3)~(4)まではEOTTI中に検出・修理が含まれるので、この期間はヒット期間(長さ=EOTTI)となります。
   

   図383.2　ヒットミス判定
   よって、$T_\text{mpfdi}\gt T_\text{eotti}$の場合はミス率、ヒット率は以下のように求められます。 $$ \Pr\{\text{miss}\}=\frac{\text{(1)~(2)までの時間間隔}}{\text{(1)~(4)までの時間間隔}}=\frac{T_\text{mpfdi}-T_\text{eotti}}{T_\text{mpfdi}}=1-\frac{T_\text{eotti}}{T_\text{mpfdi}}\tag{383.1} $$ $$ \Pr\{\text{hit}\}=\frac{\text{(3)~(4)までの時間間隔}}{\text{(1)~(4)までの時間間隔}}=\frac{T_\text{eotti}}{T_\text{mpfdi}}\tag{383.2} $$

なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。

前のブログ 次のブログ

MPF detectedへの変更の再計算した結果を表を用いてまとめます。

$$ \text{ただし、} \begin{cases} \alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ \beta:=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \end{cases}\\ \begin{cases} \begin{eqnarray} 非冗長系の時は\color{red}{K_\text{IF,det}}&=&1\\ 冗長系の時は\color{red}{K_\text{IF,det}}&=&0, K_\text{IF,RF}=1\\ \end{eqnarray} \end{cases} $$

表374.1に対して、非冗長系、冗長系のKパラメータを上記に示すとおり代入した表を表374.2及び表374.3に示します。

非冗長系

$$ M_\text{PMHF,NRD}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\alpha}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_{\text{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau] \tag{374.1}$$

冗長系

$$M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}=\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\tag{374.2}$$

$\dagger$規格式1: 規格第1版 Part 10-8.3.3の第1式の条件。ブログの図367.1)において、IFが後にフォールトする場合=(a)SPF、(b)SPF及び(c)DPF。(d)DPFはSMが後にフォールトする場合なので対象外
$\dagger$規格式3: 規格第1版 Part 10-8.3.3の第3式の条件。ブログの図367.1)において、IF, SMのフォールトの順を問わない場合=(a)SPF、(b)SPF、(c)DPF及び(d)DPF。

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ

よって、MPF detectedを考慮した場合のPMHFは、それぞれの事象は排他であることから、(369.6)、(370.5)、(371.6)、(372.5)で求められた平均PUDを全て加えることで求められ、 $$ \begin{eqnarray} \require{cancel} M_\text{PMHF}&=&\overline{q_\mathrm{SPF(a),IFU}}+\overline{q_\mathrm{SPF(b),IFR}}+\overline{q_\mathrm{DPF(c),IFR}}+\overline{q_\mathrm{DPF(d), IFR}}\\ &=&(1-K_\text{IF,RF})\lambda_\text{IF}-\bcancel{(1-K_\text{IF,RF})\alpha}\qquad\qquad\qquad\img[-0.25em]{/images/left-arrow.png}(a)\\ & &+\bcancel{(1-K_\text{IF,RF})\alpha}\quad\qquad\qquad\qquad\qquad\qquad\qquad\img[-0.25em]{/images/left-arrow.png}(b)\\ & &+K_{\text{IF,RF}}\color{red}{K_\text{IF,det}} \alpha+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta\quad\qquad\img[-0.25em]{/images/left-arrow.png}(c)\\ & &+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta\quad\qquad\qquad\qquad\qquad\qquad\img[-0.25em]{/images/left-arrow.png}(d)\\ &=&\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\alpha+2K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta}\\ &=&(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_{\text{IF,RF}}\color{red}{K_\text{IF,det}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ & &+K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau],\\ \end{eqnarray}\tag{373.1} $$

$$ ただし、\begin{cases} \begin{eqnarray} \alpha&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau],\\ \beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau],\\ K_{\mathrm{MPF}}&:=&K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}} \end{eqnarray} \end{cases} $$ この一般式に対して場合分けを行って、

1. 非冗長系においては抑止されるフォールトは全て検出可能なので、(373.1)において$K_\text{IF,det}=1$とすれば$\beta$の項が消去され、 $$ M_\text{PMHF,NRD}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\alpha}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_\text{IF,RF}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau] \tag{373.2} $$

2. 冗長系においては抑止されるフォールトは(1st SMでは)全て検出不可であり、逆に全て抑止されるため、(373.1)において$K_\text{IF,det}=0, K_\text{IF,RF}=1$とすれば$\alpha$の項が消去され、 $$ M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}=\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{MPF})T_\text{lifetime}+K_\mathrm{MPF}\tau] \tag{373.3} $$

このように、非冗長系と冗長系に対するPMHF式が導出されます。

上記場合分け1.の非冗長系の(373.2)は、DPF項は変更前の1/2になっています。これはIFのLFが無くなり、SMのLFのみになったためです。SMのLF量は変わらないため、1/2になります。

上記場合分け2.の冗長系においては、そもそもMPF detectedが無いため、変更前と結果は変わりません。

RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

前のブログ 次のブログ