|
22 |
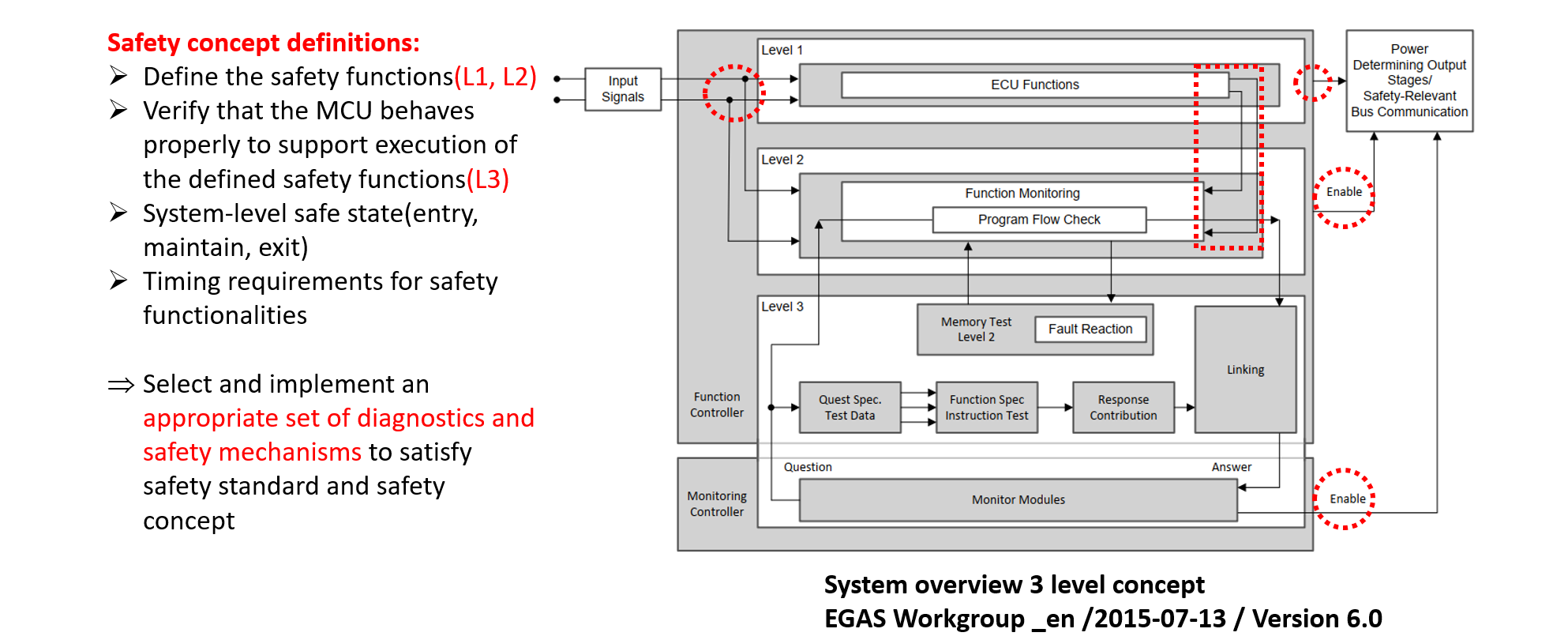
EGASアーキテクチャ (2) |
 |
2エレメントで3層構造を持つアーキテクチャの特徴を詳述してください。
ChatGPT:
以下では、EGAS(電子スロットル制御)システムに代表される「2エレメントで3層構造を持つアーキテクチャ」を例に、各層・各要素がどのように安全性を確保しているかを詳述します。なお「2エレメント」とは主にメイン系(Main)とモニタ系(Monitor)の2経路をもつことを指し、「3層構造」はセンサ入力層・制御(演算)層・アクチュエータ出力層の3段階にわたって安全を確保する仕組みを指します。
1. 全体像と目的
2エレメント(二重構成)
メイン系とモニタ系の2経路(あるいは2要素)を用意し、一方の故障を他方が検出して安全な状態に導くことが主眼となります。例えばメイン系がアクセル開度やエンジントルクを計算し、モニタ系が常時メイン系の出力値と自身で計算した値を比較することで、誤作動を即座に検出する構造です。3層構造(入力-制御-出力)
典型的には以下の3つの層に分けて、それぞれで冗長性や診断を組み込みます。- 入力層: ペダル位置センサ、スロットル位置センサなど
- 制御層: マイクロコントローラ(メイン系とモニタ系)、ソフトウェア
- 出力層: スロットルバルブアクチュエータ、あるいは燃料噴射系など
各層ごとに故障診断(監視)やフェイルセーフを組み合わせることで、高いASIL(Automotive Safety Integrity Level)要求にも対応可能なアーキテクチャを構築します。
2. 入力層 (Sensor Layer)
- 二重化センサ
- アクセルペダル(APS: Accelerator Pedal Position Sensor)やスロットルバルブ位置(TPS: Throttle Position Sensor)などのセンサを、
$$ 2 \text{系} \quad (\text{例: } \text{APS}_1, \text{APS}_2) $$ のように二重化(あるいは多重化)して設置します。 - それぞれのセンサが出力する値を常時比較し、異常(出力の大きな乖離など)を検出した際には、メイン系・モニタ系のソフトウェアが安全状態(リミット制御やフェイルセーフ)に移行するようになっています。
- アクセルペダル(APS: Accelerator Pedal Position Sensor)やスロットルバルブ位置(TPS: Throttle Position Sensor)などのセンサを、
- 入力信号の妥当性チェック
- メイン系マイコンとモニタ系マイコンの双方が、二重化センサから取得した信号に対して妥当性チェックを行います。
- $(\text{APS}_1) $と$ (\text{APS}_2) $の差分が規定値以上なら警報やデグレードモード(パワー制限)へ移行するなど、安全に関する振る舞いをソフトウェア設計上で定義します。
3. 制御層 (Control/Computation Layer)
- メイン系 (Main) とモニタ系 (Monitor)
- メイン系:
通常のエンジントルク演算、アクセル開度演算などを実施するメインのマイクロコントローラ(あるいはCPUコア)。実際にスロットルバルブや燃料噴射量などを決定します。 - モニタ系:
メイン系の演算結果が妥当かを常時監視するサブマイクロコントローラや第二のCPUコア。モニタ系は簡易的な演算(例: アクセル開度→トルクのざっくりとした見積もり)を並行して行い、メイン系の出力を比較・検証します。
- メイン系:
- クロスチェックと故障検知
- 同一センサ情報の独立演算
モニタ系もメイン系とは独立した方法または簡易モデルで同一センサ情報を演算し、メイン系の出力とのクロスチェックを実施します。 - ウォッチドッグ(Watchdog)やタイマベースの監視
メイン系・モニタ系の処理が停止したり暴走した場合に、ウォッチドッグタイマがリセットや出力無効化を指示し、出力層を安全側に移行させる仕組みを備えます。
- 同一センサ情報の独立演算
- ソフトウェアレイヤの多層防御
- AUTOSARなどのソフトウェアプラットフォームを使用する場合、BSW(Basic Software) レイヤとASW(Application Software) レイヤでそれぞれ診断機能を実装します。
- メモリ保護機構やプログラムフロー監視など、ハードウェア機能(例: Lockstep CPU、ECC保護つきメモリ)とも連携してソフトウェアの破損・暴走を検知します。
4. 出力層 (Actuator Layer)
- スロットルアクチュエータの冗長化・診断
- 出力段であるスロットルアクチュエータには、ポジションセンサを二重化するなどしてアクチュエータ内部でも故障を検知できるようにします。
- モニタ系がスロットルアクチュエータの目標値と実際の開度を比較し、大きな差異が生じた場合は出力を制限する(リミット制御)またはアイドル状態に強制移行させるなどのフェイルセーフを実行します。
- 電源制御やリレーによるフェイルサイレント化
- 出力ドライバの電源ラインに安全リレーやFETスイッチなどを設け、システムが致命的な異常と判断した場合には強制的に駆動信号を遮断します(フェイルサイレント化)。
- 遮断後はエンジン出力を絞ったり、アクセル操作が反映されない状態にすることで車両の安全を確保します。
5. アーキテクチャがもたらす安全メリット
- 単一点故障への耐性
いずれか1つのセンサやマイコンに故障が生じても、もう一方の正常系(メイン系またはモニタ系)で検知し、安全動作へ移行できる。 - 潜在的な故障の早期検知
クロスチェック(メイン系 vs モニタ系)により、たとえソフトウェアバグやメモリエラーなどの故障モードでも異常値を早期発見しやすい。 - ASIL Dレベルへの適合が容易
エンジン制御のような安全度要求の高い機能ではASIL Dが割り当てられる場合が多いが、2エレメント3層構造によって冗長性と故障検出率を高めることで、ISO 26262の厳しい要求を満たす設計を行いやすい。
6. まとめ
「2エレメントで3層構造を持つEGASアーキテクチャ」は、入力(センサ)・制御(マイコン)・出力(アクチュエータ)の各層において冗長化と診断機構を備え、かつメイン系とモニタ系という2つの経路で相互監視を行う仕組みです。これにより、単一点故障やソフトウェア異常を検出・隔離し、必要に応じて車両を安全状態に導くことが可能となります。ISO 26262で要求される高いASIL(特にCやD)にも適合するために、多層的な安全策が組み込まれるのが最大の特徴です。
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。