|
7 |
RAMS 2025での論文発表と最優秀論文賞の受賞 |
 |

過去記事に記載のとおり、RAMS 2025は、2025年1月27日から30日まで、米国フロリダ州ミラマービーチのヒルトンサンデスティンホテルで開催されました。弊社代表は2日目に論文発表を行いました。

本論文のタイトルは、"Point Unavailability and its Density Processes with Periodic Inspections in ISO 26262"です。邦題は「ISO 26262における定期検査を伴う点不稼働度とその密度過程」となります。
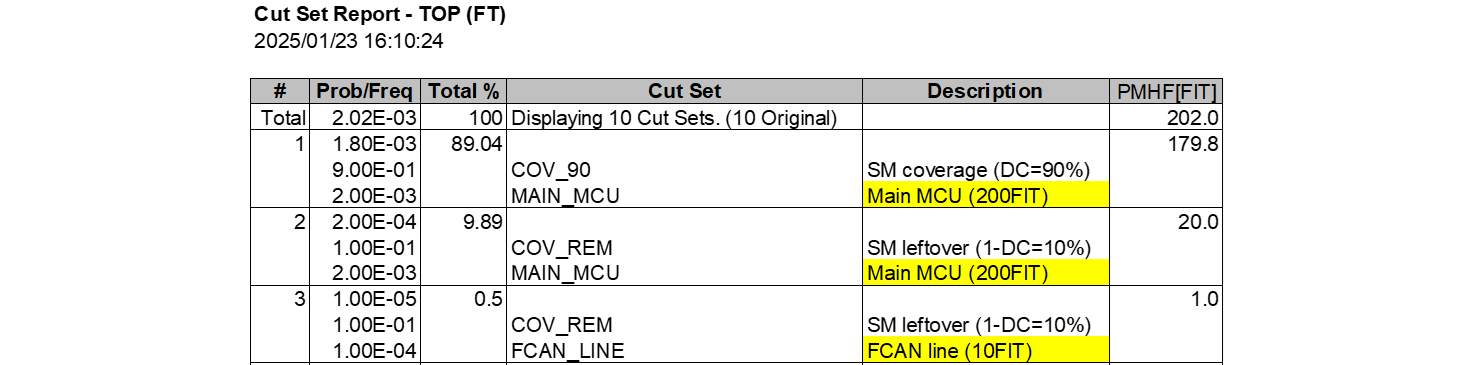
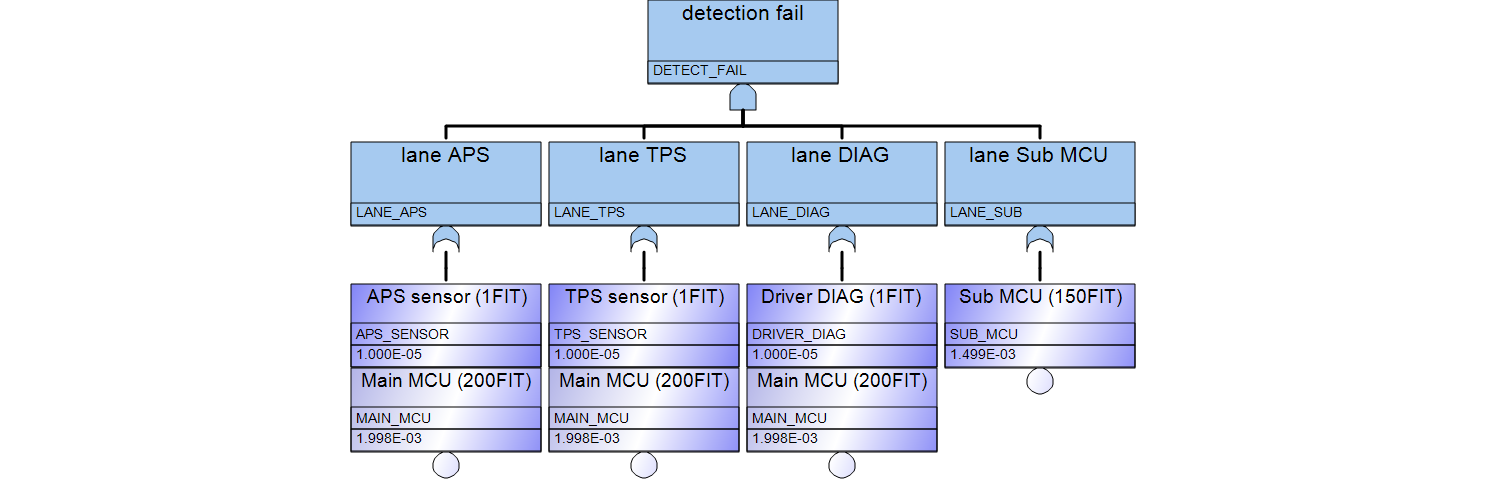
弊社が2020年のRAMSで提案したPMHFは、不稼働度または不稼働密度関数により定義されます。当時は定期検査の診断率をアーキテクチャ依存の定数と仮定し、不稼働度を導出しました。当時はこれを近似式と認識していましたが、今回診断率を条件付き確率に変更したうえで不稼働度の厳密式を導出しました。さらに誤差評価を行った結果、ASIL-Bの条件において両者にはほとんど差が無いことが分かりました。
また、弊社代表の、昨年2024年の論文がAlfred Stevens/Henry Hartt最優秀論文賞を受賞し、バンケットにおいて賞金として500ドルが授与されました。これは今回新設された賞で、本論文がISO 26262規格の誤りを明らかにしたことが評価されたものです。