Fault Treeの構成

PMHF式に準拠してFault Tree (FT)を構成します。まず基礎となるFTは図929.1のとおりです。このFT構成法は弊社の過去論文に依るものです。これは後で示すPMHF式を再現するように構成しています。

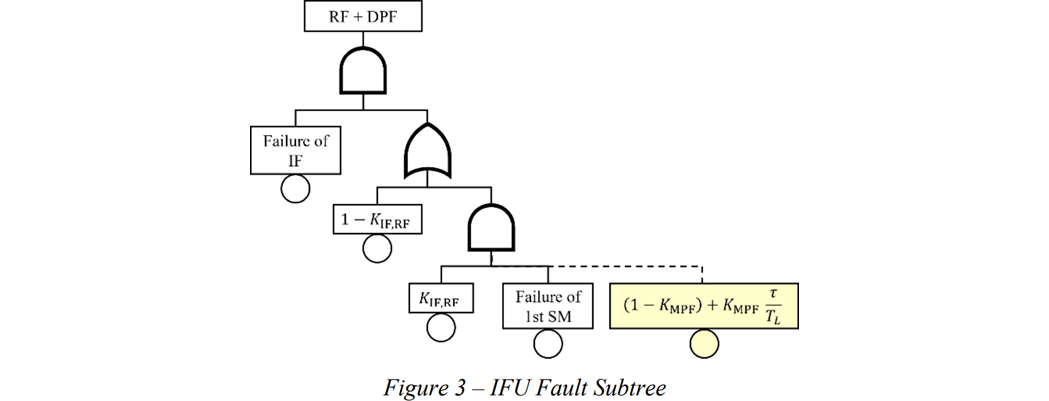
次に対応するPMHF式を示します。前記FTの構成法にはMethod 1, 2, 3と3種あり、それぞれ以下のような特徴があります。

• Method 1: 2nd SMが無いものとする。もっとも単純なツリーであり、真値よりもPMHFは大となるため、初期にワーストケースを見るのに都合が良い。 $$ M_\text{PMHF}=(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM} $$
• Method 2: 2nd SMのカバレージ$K_\text{SM,MPF}$の効果を加えたもの。ただし、真値よりも次のMethod 3で加わる効果が入っていない分だけPMHFが小さく算出されることが問題。ただしこの誤差は$K_\text{SM,MPF}$が小さい時または$\tau$が小さい時は無視できる。 $$ M_\text{PMHF}=(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\color{red}{\left((1-K_\text{SM,MPF})T_\text{lifetime}\right)} $$
• Method 3: Method 2の効果に加えて、2nd SMの定期検査周期間$\tau$内の不検出効果を加える。PMHFとしては真値であるが、加えた不検出効果は、$K_\text{SM,MPF}$が小さい時または$\tau$が小さい時は無視できる。 $$ M_\text{PMHF}=(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\left((1-K_\text{SM,MPF})T_\text{lifetime}\color{red}{+K_\text{SM,MPF}\tau}\right) $$

Method 3の係数の効果を3Dグラフに表すと図929.2のような形になります。

$$\img[-1.35em]{/images/withinseminar.png}$$

記事#927で述べたように、$K_\text{MPF}$が小さいか$\tau$が小さい場合にはこの効果は無視できます。

なお、本稿はRAMS 2028に投稿予定のため一部を秘匿していますが、論文公開後の2028年2月頃に開示予定です。

前のブログ 次のブログ