StmtFSM

前稿ではBSVにより、ステートベースのFSMを設計しました。ステートベースとは、シーケンスを人手でステートに分解し、一つ一つのステートに対してルールを書くもので、基本的にはverilogと同程度の工数がかかります。一方、BSVにはステートマシンを効率的に設計できる、StmtFSMというライブラリが存在します。

検証用FSM

このライブラリの検証用のために検証用FSMを作成します。検証用FSMは2つのコンカレントなFSMを持ち、一方のSenderFSMがFIFOにデータを詰め(エンキュー)、他方のReceiverFSMがFIFOからデータを取り出す(デキュー)ものとします。コンカレントであり、エンキューとデキューは同時に起こります。

図251.1 センダーFSMとレシーバーFSM FSMはそれぞれ別に書き、その内部ではステートメントはシーケンシャルに実行されます。このシーケンシャルの動きはBSCにより管理され、隠れた(設計者から見えない)ステートが割り付けられます。以下にBSVのコードを示します。

package Tb;
import StmtFSM::*;
import FIFOF::*;

(* synthesize *)
module mkTb (Empty);
   FIFOF#(Bit#(8)) fifo <- mkFIFOF;

   Stmt sender =
      seq
         $display("senderFSM  %4d FSM started", $time);
         action
            $display("senderFSM  %4d Enq 10", $time);
            fifo.enq(10);
         endaction
         action
            $display("senderFSM  %4d Enq 20", $time);
            fifo.enq(20);
         endaction
         action
            $display("senderFSM  %4d Enq 30", $time);
            fifo.enq(30);
         endaction
         repeat (8) noAction;
      endseq;

      FSM senderFSM <- mkFSM(sender );

      Stmt receiver =
         seq
            $display("receiverFSM %4d receiver FSM started", $time);
            while(True) seq
               action
                  $display("receiverFSM %4d FIFO popped data", $time, fifo.first());
                  fifo.deq();
               endaction
               repeat (2) noAction;
            endseq
         endseq;

         FSM receiverFSM <- mkFSM(receiver);

      rule startit;
         senderFSM.start();
         receiverFSM.start();
      endrule

      rule finish (senderFSM.done() && !receiverFSM.done());
         $finish;
      endrule
   endmodule
endpackage

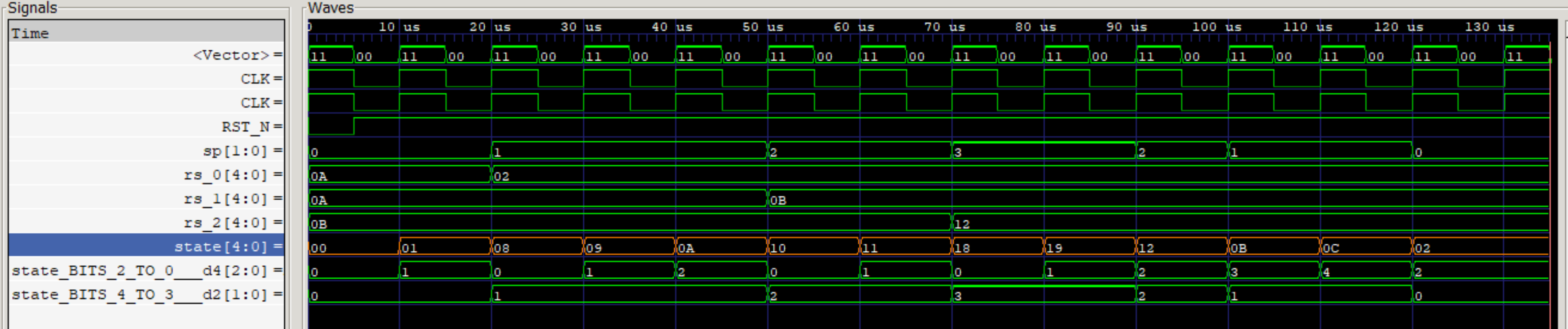
コードに示すように、エンキューはレイテンシ1で実行され、デキューはレイテンシ3で実行されます。各々のFSMは、エンキューデータ、デキューデータをそれぞれ表示します。

---

前のブログ 次のブログ

レジスタ配列によるリターンスタック

前稿のリターンスタックrsはベクター配列で構成しましたが、最初に戻りレジスタ配列を試してみます。当初から配列で試したところ、うまく行っていませんでしたが、成功したのでその方法を記述します。まずリターンスタックrsを配列宣言します。

   // return stack
   Reg#(State_t) rs[3];

次に、リターンスタックrsを3段レジスタによりインスタンシエートします。これが無かったため、今まで動作しませんでした。ちなみにverilogでは宣言しただけで使用できますが、BSVでは宣言し、次にインスタンシエートが必要です。

   for (int i = 0; i < 3; i = i + 1)
      rs[i] <- mkRegU;

マクロ命令定義はベクター配列と同じ配列によるアクセス法を用います。

`define call(SUB)                    `_pushNext; state <= State_t {func:SUB, step:S0}
`define _pushNext                   rs[sp] <= State_t {func:state.func, step:nextStep()}; sp <= sp + 1
`define return                          state <= rs[sp-1]; sp <= sp - 1
`define next                             state.step <= nextStep()

説明は表248.1と同一です。これを用いて、前稿の検証FSMを実行してみます。

\$ bsc -sim -u TestFSM4.bsv
checking package dependencies
compiling TestFSM3.bsv
code generation for mkTestFSM starts
Elaborated module file created: mkTestFSM.ba
All packages are up to date.
\$ bsc -sim -e mkTestFSM -o mkTestFSM
Bluesim object created: mkTestFSM.{h,o}
Bluesim object created: model_mkTestFSM.{h,o}
Simulation shared library created: mkTestFSM.so
Simulation executable created: mkTestFSM
\$ ./mkTestFSM -m 15 -V dump.vcd | tee result
L1 S0
L1 S1
　L2 S0
　L2 S1
　L2 S2
　　L3 S0
　　L3 S1
　　　L4 S0
　　　L4 S1
　　L3 S2
　L2 S3
　L2 S4
L1 S2
L1 S2
\$

正しく実行することが検証できました。波形を図250.1に示します。内部信号を見ると、ベクター配列と同様、rs_0, rs_1, rs_2という3個のレジスタインスタンスが生成されています。

図250.1 検証用FSMのBsim波形(レジスタ配列使用)

合成結果

Vivadoによる合成結果は21 LUTのサイズでした。レジスタ配列とベクター配列は同様のサイズであったため、今後は最も素直なこの方式を採用します。

ソフトウェアの場合は高速なレジスタと低速なメモリがあるため、リターンレジスタ等の実装が必要ですが、FSMではよほどのことが無い限り全てレジスタなので、リターンレジスタを使用しない、この実装を基本的に使用していきます。

---

前のブログ 次のブログ

ベクター配列によるリターンスタック

前稿までのリターンスタックrsはレジスタファイルで構成しましたが、別法のベクター配列を試してみます。 まずベクターをインポートします。

import Vector::*;

次に、リターンスタックrsを3段インスタンシエートします。

   // return stack
   Vector#(3, Reg#(State_t)) rs <- replicateM(mkRegU);

さらにマクロ命令定義を書き換えます。ベクター配列はrs[sp]として扱えるので、直感的に分かりやすいです。

`define call(SUB)                    `_pushNext; state <= State_t {func:SUB, step:S0}
`define _pushNext                   rs[sp] <= State_t {func:state.func, step:nextStep()}; sp <= sp + 1
`define return                          state <= rs[sp-1]; sp <= sp - 1
`define next                             state.step <= nextStep()

説明は表248.1と同一です。これを用いて、前稿の検証FSMを実行してみます。

\$ bsc -sim -u TestFSM3.bsv
checking package dependencies
compiling TestFSM3.bsv
code generation for mkTestFSM starts
Elaborated module file created: mkTestFSM.ba
All packages are up to date.
\$ bsc -sim -e mkTestFSM -o mkTestFSM
Bluesim object created: mkTestFSM.{h,o}
Bluesim object created: model_mkTestFSM.{h,o}
Simulation shared library created: mkTestFSM.so
Simulation executable created: mkTestFSM
\$ ./mkTestFSM -m 15 -V dump.vcd | tee result
L1 S0
L1 S1
　L2 S0
　L2 S1
　L2 S2
　　L3 S0
　　L3 S1
　　　L4 S0
　　　L4 S1
　　L3 S2
　L2 S3
　L2 S4
L1 S2
L1 S2
\$

正しく実行することが検証できました。波形を図249.1に示します。内部信号を見ると、rs_0, rs_1, rs_2という3個のレジスタインスタンスが生成されています。これが3段のリターンスタックを構成しています。

図249.1 検証用FSMのBsim波形(ベクター配列使用)

合成結果

Vivadoによる合成結果は21 LUTのサイズでした。レジスタファイルよりもベクター配列のほうが、わずかに小さくなることが分かりました。レジスタファイルは下位モジュールのレジスタファイルをインスタンスする必要がありますが、ベクター配列は上記のようにレジスタが展開されるだけです。従って、インタフェースが簡略化されるため、小さくなると考えられます。

---

前のブログ 次のブログ

マクロ命令定義

以上の議論から再定義したマクロ命令のコードです。

`define call(SUB)                    `_pushNext; state <= State_t {func:SUB, step:S0}
`define _pushNext                   rs.upd(sp, State_t {func:state.func, step:nextStep()}); sp <= sp + 1
`define pushCall(FUNC,SUB)  _pushFunc(FUNC); state <= State_t {func:SUB, step:S0}
`define _pushFunc(FUNC)      rs.upd(sp, State_t {func:FUNC, step:S0}); sp <= sp + 1
`define nextFunc                    state <= State_t {func:nextFunc(), step:S0}
`define return                          state <= rs.sub(sp-1); sp <= sp - 1
`define next                             state.step <= nextStep()

今回、アプリ(インベーダサウンドFSM)の必要上pushCallを定義しています。これは、call命令の一般化であり、次ステートではなく任意のファンクションに戻るコールを実装するものです。以上のマクロ命令の説明を表248.1に示します。

表248.1　マクロ命令の説明

マクロ命令名	説明
call(SUB)	サブルーチンコールです。次ステートをプッシュして、サブルーチンSUBをコールします。
_pushNext	callに使用されており、次のステートをプッシュする内部マクロ命令です。nextStep()関数を使用しています。ユーザは陽に使う必要は無いため、先頭にアンダースコアを付けています。
pushCall(FUNC,SUB)	サブルーチンコールです。戻り先ファンクションFUNCをプッシュして、サブルーチンSUBをコールします。戻り先は指定されたファンクションFUNCの先頭S0となります。
_pushFunc(FUNC)	pushCallに使用されており、戻り先ファンクションFUNCをプッシュする内部マクロ命令です。ユーザは陽に使う必要は無いため、先頭にアンダースコアを付けています。
nextFunc	次のファンクションに進めるためのマクロ命令です。nextFunc()関数を使用しています。
return	呼び出し元(の次のステート)に戻るためのマクロ命令です。
next	次のステートに進めるためのマクロ命令です。nextStep()関数を使用しています。

合成結果

Vivadoによる合成結果は22 LUTのサイズでした。

---

前のブログ 次のブログ

リファクタリング(1)(プッシュとリターンの統合)

前稿でpushRetとcallをまとめるアイデアを記載しましたが、それを実装してみます。まとめたマクロ命令をpushCallと名付けます。

`define _pushRet             rs.upd(sp, ret); sp <= sp + 1
`define popRet                 state <= rs.sub(sp-1); sp <= sp - 1
`define pushCall(SUB)     `_pushRet; `_saveNext; state <= State_t {func:SUB, step:S0}
`define _saveNext            ret <= State_t {func:state.func, step:nextStep()}
`define return                   state <= ret

非リーフでのコールとリターンが完成したので動作確認を行います。非リーフでのcallをpushCallに、リターンはそのままpopRetとします。リーフではcallは無く、リターンはそのままreturnとします。

ソースコード内のpushRetを削除し、それぞれのcallをL1ルール内において、

         `pushCall(L2);

L2ルール内において、

         `pushCall(L3);

L3ルール内において、

         `pushCall(L4);

のように修正します。動作確認した結果、expectedと一致し正常動作が確認されました。

リファクタリング(2)(リーフと非リーフの共通化)

そもそもリターンレジスタのretがあるためリーフと非リーフの区別がありました。スタック操作はハードウエアであり、性能へのインパクトがほとんど無いことから、リーフ・非リーフで統一したやり方を考えます。それにはretレジスタを廃止します。従って、callとreturnは以下のようにリターンスタックのみで操作します。 retレジスタの削除の他、マクロの修正を次のように行います。

`define return                state <= rs.sub(sp-1); sp <= sp - 1
`define call(SUB)          `_pushNext; state <= State_t {func:SUB, step:S0}
`define _pushNext        rs.upd(sp, State_t {func:state.func, step:nextStep()}); sp <= sp + 1
`define next                  state.step <= nextStep()

としました。これにより、サブルーチンコールの場合は常にcall()を用い、リターンの場合は常にreturnを用います。このように修正した結果、正常動作することを確認しました。ただし、returnレジスタを削除したため、rsはL1~L3で使用により3段、従ってspは2bitとなりました。

以上から、内部マクロを除くユーザーに見えるマクロは、call()、return、nextの3種となります。

---

前のブログ 次のブログ

コンパイルと実行

ソースプログラムをコンパイルします。

$ bsc -u -sim TestFSM.bsv
checking package dependencies
compiling TestFSM.bsv
code generation for mkTestFSM starts
Elaborated module file created: mkTestFSM.ba
All packages are up to date.

次にリンクします。

$ bsc -sim -e mkTestFSM -o mkTestFSM
Bluesim object created: mkTestFSM.{h,o}
Bluesim object created: model_mkTestFSM.{h,o}
Simulation shared library created: mkTestFSM.so
Simulation executable created: mkTestFSM

15サイクル実行します。

$ ./mkTestFSM -V dump.vcd -m 15 | tee result
L1 S0
L1 S1
　L2 S0
　L2 S1
　L2 S2
　　L3 S0
　　L3 S1
　　　L4 S0
　　　L4 S1
　　L3 S2
　L2 S3
　L2 S4
L1 S2
L1 S2
$

検証結果

結果を比較することにより検証します。

$ diff -c result expected
$

出力結果がサイクルベースで一致したことにより、正しく動作していることが検証されました。実は階層が4レベルあってもL1では戻り先が無いのでスタックを使いませんし、L4もリーフなのでスタックを使いません。従ってL2とL3だけでpush/popするため、スタックは2段(retを含めて3段)となり、spは1bitで良いことになります。これはたまたま前稿と同じ設計です。

このように変更し、上記のコンパイル、実行、一致検証まで実施したところ、期待した動作をすることが確認されました。rsが2段の場合のBsimの波形を図246.2に示します。spは1bitしかないので、sp==2の際にsp==0という不正な値となっていますが、sp==2の場合のspは使用しないため、問題ありません。

図246.2 検証用FSMのBsim波形 次にiverilogによるVerilogシミュレーション波形を図246.3示します。Bsimではrsを見ることができませんでしたが、verilogでは下位モジュールにrsがRAMとして配置されるので、push時にはステート'h08(L2 S0)とステート'h10(L3 S0)の2回、RAMのWEがアサートされていることが分かります。 図246.3 検証用FSMのIverilog波形

---

前のブログ 次のブログ

マクロ命令の使用

過去記事のCalee Savedコールリターンを前稿で作成したマクロ命令を使用して書き直すと、図245.1のようになります。青字がマクロ命令です。Caller Savedでは入らなかった余分なpushRetがルーチン先頭に入っています。あるいは次のcallとまとめてしまい、非リーフからのcallを別に設ければこれは見かけ上無くなります。こうすれば、リーフと非リーフで、コールもリターンも別になるのでかえってすっきりするかもしれません。

図245.1 マクロ命令を使用したサブルーチン呼び出し

検証用FSMソースコード

検証用FSMのBSVの全ソースコードを示します(既紹介部分は除く)。

import RegFile::*;

(* synthesize, always_ready, always_enabled *)
module mkTestFSM();

   Reg#(State_t) state <- mkReg(State_t{func:L1, step:S0}),
                 ret <- mkRegU;

   // L1
   rule rule_L1 (state.func == L1);
      rule rule_S0 (state.step == S0);
         $display("L1 S%d", state.step);
         `next;
      endrule // S0
      rule rule_S1 (state.step == S1);
         $display("L1 S%d", state.step);
         `call(L2);
      endrule // S1
      rule rule_S2 (state.step == S2);
         $display("L1 S%d", state.step);
      endrule // S2
   endrule // L1

   // L2
   rule rule_L2 (state.func == L2);
      rule rule_S0 (state.step == S0);
         $display("  L2 S%d", state.step);
         `pushRet; // L2 is not a leaf routine
         `next;
      endrule // S0
      rule rule_S1 (state.step == S1);
         $display("  L2 S%d", state.step);
         `next;
      endrule // S1
      rule rule_S2 (state.step == S2);
         $display("  L2 S%d", state.step);
         `call(L3);
      endrule // S2
      rule rule_S3 (state.step == S3);
         $display("  L2 S%d", state.step);
         `next;
      endrule // S3
      rule rule_S4 (state.step == S4);
         $display("  L2 S%d", state.step);
         `popRet;
      endrule // S4
   endrule // L2

   // L3
   rule rule_L3 (state.func == L3);
      rule rule_S0 (state.step == S0);
         $display("    L3 S%d", state.step);
         `pushRet; // L3 is not a leaf routine
         `next;
      endrule // S0
      rule rule_S1 (state.step == S1);
         $display("    L3 S%d", state.step);
         `call(L4);
      endrule // S1
      rule rule_S2 (state.step == S2);
         $display("    L3 S%d", state.step);
         `popRet;
      endrule // S2
   endrule // L3

   // L4 (Leaf)
   rule rule_L4 (state.func == L4);
      rule rule_S0 (state.step == S0);
         $display("      L4 S%d", state.step);
         `next;
      endrule // S0
      rule rule_S1 (state.step == S1);
         $display("      L4 S%d", state.step);
         `return;
      endrule // S1
   endrule // L4

endmodule: mkTestFSM

---

前のブログ 次のブログ

BSVコード

nextStep()関数は以下のとおりです。

function nextStep;
   case (state.step)
      S0: nextStep = S1;
      S1: nextStep = S2;
      S2: nextStep = S3;
      S3: nextStep = S4;
   endcase
endfunction: nextStep

以下に4段のスタックとスタックポインタの実装(インスタンシエーション)を示します。

// return stack
RegFile#(UInt#(2), State_t) rs <- mkRegFile(0, 3);
// stack pointer
Reg#(UInt#(2)) sp <- mkReg(0);

検証用FSMの設計

これらのステート遷移の検証用FSMを設計します。全部でL1~L4の4レベルのコールネスティング関係を持ち、各ステートでは、主にステート変数の表示を行います。図244.1～図244.4に、レベル1からレベル4のステート遷移図を図示します。

図244.1 L1ステート遷移

図244.2 L2ステート遷移

図244.3 L3ステート遷移

図244.4 L4ステート遷移

検証結果の作成

expectedというファイル名で実行結果を作成しておきます。レベルとステートをサイクル毎に表示するFSMの動きを示します。

L1 S0
L1 S1
  L2 S0
  L2 S1
  L2 S2
    L3 S0
    L3 S1
      L4 S0
      L4 S1
    L3 S2
  L2 S3
  L2 S4
L1 S2
L1 S2

---

前のブログ 次のブログ

スタック操作のBSV記述

共通シーケンスをコールする場合、これまで見てきたように、スタック操作をする必要がありますが、煩雑なのでこれを隠蔽することを考えます。と言ってもソフトウェアでやるように、push, pop, call, return等の概念を使います。また、これまでハードウェアという意識から「共通シーケンス」と称してきた概念を、ソフトウエアに合わせてサブルーチンと呼びます。

対象となる検証用FSMのステート定義を示します。例として4レベルのFSMを考えます。state変数は構造体で定義しています。

typedef enum { L1, L2, L3, L4 } Function_t deriving(Bits,Eq);
typedef enum { S0, S1, S2, S3, S4 } Step_t deriving(Bits,Eq);

typedef struct {
   Function_t func;
   Step_t step;
} State_t deriving(Bits,Eq);

rsはリターンスタック配列で、BSVでの実装例として、今回はRegFileで構成します。spはスタックポインタで配列インデックスです。Verilogにおける配列のdata変数への読み出し

data <= rs[sp]

は、この実装では、

data <=rs.sub(sp)

となり、逆にVerilogにおける配列へのdataの書き込み

rs[sp] <= data

は、この実装では

rs.upd(sp, data)

となります。

マクロ命令定義

これらを用いて作成したマクロ命令の定義文のコードです。

`define pushRet             rs.upd(sp, ret); sp <= sp + 1
`define popRet            state <= rs.sub(sp-1); sp <= sp - 1
`define call(SUB)         `_saveNext; state <= State_t {func:SUB, step:S0}
`define _saveNext         ret <= State_t {func:state.func, step:nextStep()}
`define return                  state <= ret
`define next                    state.step <= nextStep()

その説明を表243.1に示します。

表243.1　マクロ命令の定義

マクロ命令名	説明
pushRet	非リーフルーチン中で、他のルーチンを呼ぶ際に破壊されるretをスタックにプッシュするマクロ命令で、必ず先頭でpushするものとします。
popRet	非リーフ内で呼び出し元に戻るためのマクロ命令で、retを回復せずに、スタック中の戻りステートに直接戻るマクロ命令です。
call(SUB)	サブルーチンコールです。次のステートをretに入れ、コール先にジャンプします。
_saveNext	callに使用されており、次のステートをretに入れる内部マクロ命令です。後述のnextStep()関数を使用しています。ユーザが陽に使う必要は無いため、アンダースコアを付けています。
return	リーフ内で呼び出し元に戻るためのマクロ命令です。
next	次のステートに進めるためのマクロ命令です。後述のnextStep()関数を使用しています。

---

前のブログ 次のブログ

Direct Return

ついでに前稿で検討したダイレクトリターンがどうなるかを見ておきます。まず図で書けば、前稿のCaller Savedでは図242.1のようになります。左が一般的な、非リーフからのリーフのコール、右がダイレクトリターンです。コール先がリーフであると分かっている時は、リターンレジスタに戻り先を入れる代わりに、スタックをポップして戻り先をリターンレジスタに入れてからコールします。

図242.1 Caller Savedダイレクトリターン 一方、Callee Saved方式では、図242.2のようになります。同じく、左が一般的な、非リーフからのリーフのコール、右がダイレクトリターンです。 図242.2 Calee Savedダイレクトリターン 同じくコール先がリーフであると分かっている場合には、リターンレジスタに戻り先を入れる代わりに、そのままジャンプします。コール先を見ないという利点は無いものの、処理が単純化されます。

---

前のブログ 次のブログ