|
13 |
故障率 (6) |
和文は英文の後に続きます。
(English text comes here.)
平均故障率と瞬間故障率
故障率(1)において、Excel表によって良品数$v(t)$のグラフを作成する方法をご紹介しました。(1.2)は、現在の良品数に一定の率(=故障率)をかけたものが故障数で、それを現在の良品数から引いた数により、次の時間の良品数を表す、という意味でした。 \[ v(t+1)-v(t)=-\hat{\lambda}(t)\cdot v(t) \tag{1.2} \] 故障率(2)で示した以下の(2.4)により、信頼度$R(t)$も同様な形となります。 \[ R(t+1)-R(t)=-\hat{\lambda}(t)\cdot R(t) \tag{2.4} \]
一方、故障率(5)において、故障率を一定とした場合に信頼度$R(t)$の式は、(5.2)となることを示しました。 \[ R(t)=e^{-\lambda t} \tag{5.2} \]
ここで、(2.4)によるグラフと、(5.2)のグラフが同じになるかを調べようと思います。前者が平均故障率$\hat{\lambda}$で後者が瞬間故障率$\lambda$のグラフです。
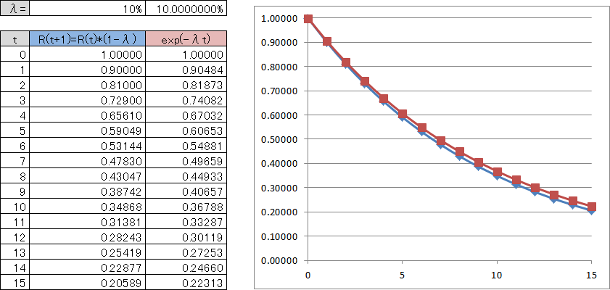
図6.1において、青が平均故障率$\hat{\lambda}=10\%$による信頼度、赤が瞬間故障率$\lambda=10\%$による信頼度です。2つのグラフはこのように、時間が進むにつれ次第に食い違いを見せます。同じ10%の故障率なのに、前者は一時間後に0.9になりますが、後者は0.90484となり、差が開いていきます。
この理由は文字どおり、前者が平均故障率で後者が瞬間故障率だからの違いによるものですが、逆に、一致するのはどういう値のときでしょうか?
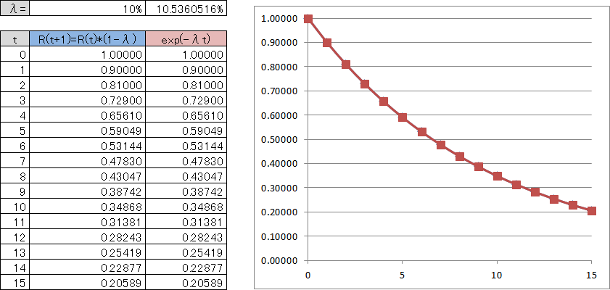
図6.2は、両グラフが一致するときの信頼度のグラフで、平均故障率$\hat{\lambda}=10\%$に対して瞬間故障率は$\lambda=10.536\%$となっています。
実は、現在値に比例して減少するのは収入とそれに対する支出も同じなのではないでしょうか。もちろん、収入が減っても食費のように減らせないものもあるかもしれませんが、それでも高い外食をしなくなったり、収入に応じた生活をするようになると思います。
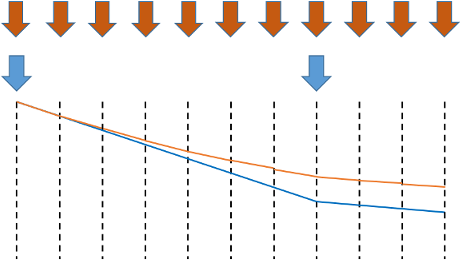
一時間の平均故障率のグラフ(青)と、瞬間故障率のグラフ(赤)を定性的に比較すると、赤のグラフのほうは、月々の貯金残高で、次の月の支出を抑える生活なのに比べて、青のグラフのほうは、一年に一度しか貯金残高を確認せずに、年初の貯金で年末まで使ってしまう生活を表しているとも見えます。当然、見直す頻度が高いほうが浪費が少ないわけで、それが青と赤のグラフの差に反映されているのではないでしょうか。
お金の話が出てきましたが、実は、故障率の符号を反転すると、時間が経つほど現在価値に比例してお金が増えていく、つまりは複利の概念と同一だということがわかります。複利だと預けておけば勝手にお金が増えますが、故障率はマイナス符号が付いているので、時間が経つと減っていきます。幸いなのは減ってくると減る絶対値も減少してくることです。

Leave a Comment