|
24 |
確率論 (21) |
今回は「確率モデル入門」(朝倉書店)からポアソン過程の部分を引用します。
確率過程
連続時間$t(\ge 0$)において確率法則が確率変数$X(t)$で表されるとき、確率変数の集まり$\{X(t),t\ge 0\}$は連続時間確率過程と呼ばれる。また、$X(t)$の取る値の集合は状態空間と呼ばれ、本稿では状態空間は離散形のみを取り扱う。
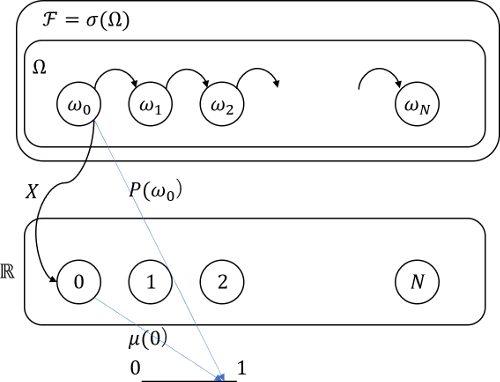
以前のポストでも確率過程を取り扱いましたが、基礎確率空間$(\Omega, \mathcal{F}, P)$において、任意の時刻$t$を固定した確率変数$X(\omega)$が$\mathcal{F}$可測となっていることが確率過程の条件となります。
計数過程
数(整数)を数える確率過程$\{N(t), t\ge 0\}$を計数過程という。
我々は$N$個の部品の故障数を数えているので、計数過程です。
独立増分過程
確率過程$\{X(t), t\ge 0\}$において、任意の$t_1\lt t_2\lt ...\lt t_n$に対し、確率変数 $$X(t_1)-X(t_0), X(t_2)-X(t_1),...,X(t_n)-X(t_{n-1})$$ が独立ならば、この確率過程は独立増分を持つという。
2項過程幾何分布
離散時間計数過程$\{N(n), n=1, 2, ...\}$において、故障確率$p (0\le p\le 1)$の試行列を考える。$N(1)=0$として、時刻$n$における故障事象の累積回数を$N(n)$とするとき、この確率過程をパラメータ$p$の2項過程幾何分布という。
この2項過程幾何分布は離散時間計数過程ですが、これを連続過程に移したらどうなるかを見てみます。時刻$0$から$t$までの時間間隔を$n$分割すれば、微小離散時間$\Delta t$は、 $$\Delta t=\frac{t}{n}$$ となり、図で表せば図198.1のようになります。

また、区間内の故障回数($\approx$故障確率)$p$を故障率$\lambda$で表せば、故障率は単位時間あたりの故障回数なので、 $$p=\lambda\Delta t=\frac{\lambda t}{n}$$ 時刻$t$の$n$回目で初めて故障が起きる確率は、各試行は独立であるため事象のANDは確率の積で表すことができるので、2項過程幾何分布より $$\Pr\{\text{item not fail in }n-1\cap \text{item fail at }n\}\\ =\Pr\{\text{item not fail in }n-1\}\Pr\{\text{item fail at }n\}=(1-p)^{n-1}p$$ となります。
ポアソン過程指数分布
$[0, t]$間での連続的な変化を考え、2項過程幾何分布において$n\to\infty, \Delta t\to 0$の極限をとります。ところが時刻$t$で初めて故障が起きる確率を求めるため、これは$P(X=t)$を求める事に対応するので、連続確率過程では確率はほとんど確実に(a.s.)$0$になります。従って、瞬間ではなく微小時間間隔$dt\to 0$での故障確率を考え、確率密度関数を$f(t)$とすれば、 $$\Pr\{X\in dt\}=\Pr\{X\in [t-dt, t)\}=\lim_{n\to\infty}(1-p)^{n-1}p\\ =\lim_{n\to\infty}\left(1-\frac{\lambda t}{n}\right)^{n-1}\lambda dt=e^{-\lambda t}\cdot \lambda dt=f(t)dt$$ よって、 $$f(t)=\lambda e^{-\lambda t}$$
$f(t)$は確率密度関数もしくはpdf(Probability Density Function)です。
連続時間での最初の故障までの確率密度関数が求められたので、これを$0$から$t$まで積分すれば、区間$[0, t]$での最初の故障の累積分布関数が求められます。最初の故障が起きるまでの時間はFFOT(Failure Free Operating Time; 無故障運転時間)とほとんど確実に(a.s.)一致します。 $$\int_0^t\lambda e^{-\lambda x}dx=1-e^{\lambda t}$$
2項過程幾何分布の連続系はポアソン過程指数分布と呼ばれ、累積分布は指数分布となります。故障はまれにしか起きない連続的な計数過程であるので、ポアソン過程指数分布でモデル化を行います。