それでは現実の回路でのトライアルを行います。まず受動部品から成るエレメントELEM1を取り上げます。 受動部品には以下のように抵抗とキャパシタが含まれます。

部品番号	部品種類	故障率[FIT]
C1000	Capacitor	0.065
C1001	Capacitor	0.065
R1000	Registor	0.011
R1001	Registor	0.011
R1002	Registor	0.011
R1003	Registor	0.011
C1010	Capacitor	0.065
C1011	Capacitor	0.065
R1010	Registor	0.011
R1011	Registor	0.011
R1012	Registor	0.011
R1013	Registor	0.011

原始シート準備

エクセルシートを新規に開き、部品情報をSheet1のA1からB12まで並べます。並べるとSheet1は以下の図のようになります。

図912.1　Sheet1の表

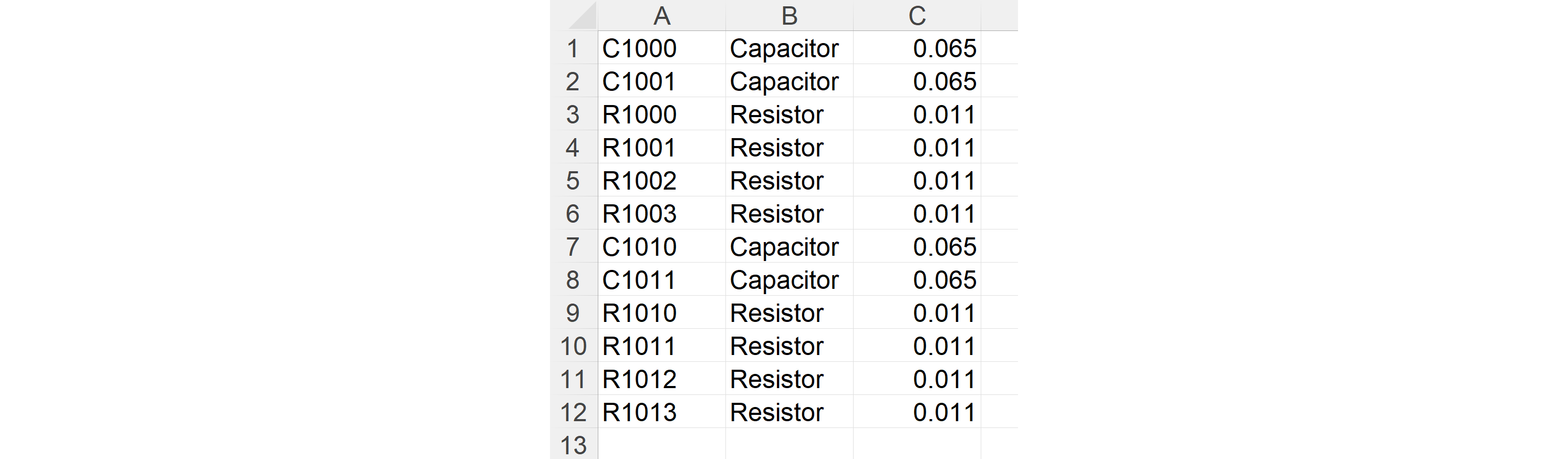
BED

準備としてSheet2に基本事象の部分を作成します。A1セルに

=IF(Sheet1!A1<>"",CONCATENATE(Sheet1!A1,", ",Sheet1!A1," ",Sheet1!B1,", TEST"),"")

この式を入れ行コピーを必要分行います。するとSheet2は以下の図のようになります。

図912.2　Sheet2の表

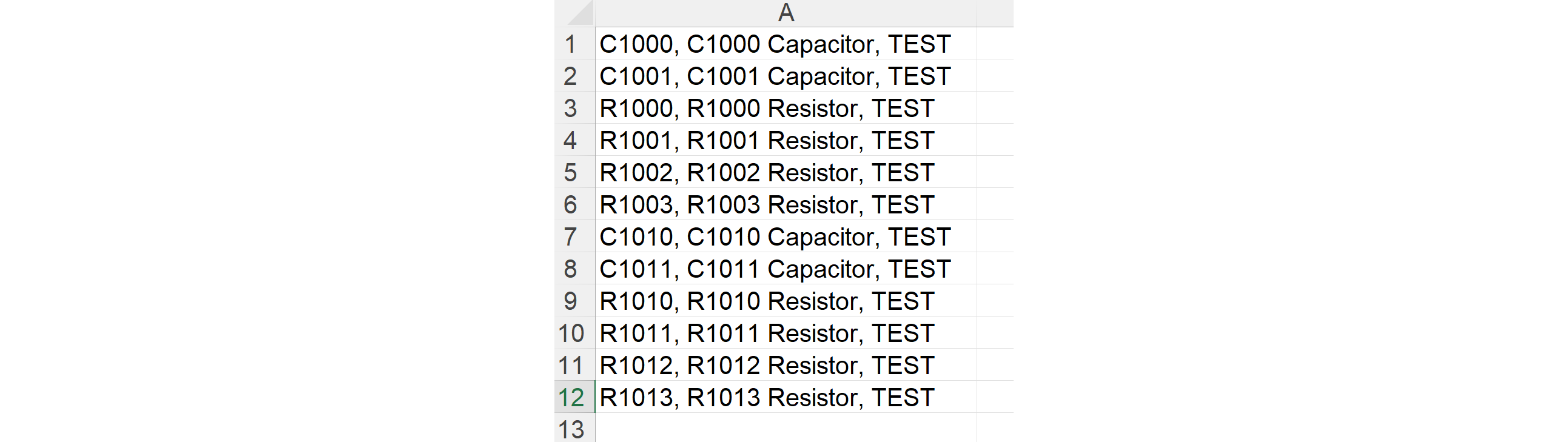
Sheet2をコピーし、以下のようにBEDファイルの* Name ...のコメント行以下にペーストします。

*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
C1000, C1000 Capacitor, TEST
C1001, C1001 Capacitor, TEST
R1000, R1000 Resistor, TEST
R1001, R1001 Resistor, TEST
R1002, R1002 Resistor, TEST
R1003, R1003 Resistor, TEST
C1010, C1010 Capacitor, TEST
C1011, C1011 Capacitor, TEST
R1010, R1010 Resistor, TEST
R1011, R1011 Resistor, TEST
R1012, R1012 Resistor, TEST
R1013, R1013 Resistor, TEST

図912.3 生成FT用BED

BEI

準備としてSheet3に基本事象情報の部分を作成します。A1セルに

=IF(Sheet1!A1<>"",CONCATENATE(Sheet1!A1, ", 3, , , 0.000E+000, 0.000E+000, ",Sheet1!C1,"E-9",", 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST"),"")

この式を入れ行コピーを必要分行います。するとSheet3は以下の図のようになります。

図912.4　Sheet3の表

Sheet3をコピーし、以下のようにBEIファイルの* Name ...のコメント行以下にペーストします。

*Saphire 8.2.9
TEST =
* Name ,FdT,UdC ,UdT, UdValue, Prob, Lambda, Tau, Mission, Init,PF, UdValue2, Calc. Prob, Freq, Analysis Type , Phase Type , Project
C1000, 3, , , 0.000E+000, 0.000E+000, 0.065E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
C1001, 3, , , 0.000E+000, 0.000E+000, 0.065E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1000, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1001, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1002, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1003, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
C1010, 3, , , 0.000E+000, 0.000E+000, 0.065E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
C1011, 3, , , 0.000E+000, 0.000E+000, 0.065E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1010, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1011, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1012, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST
R1013, 3, , , 0.000E+000, 0.000E+000, 0.011E-9, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.500E-003, ,RANDOM, CD, TEST

図912.5 生成FT用BEI

FTD

FTDは他のファイルと同一の以下のようなファイルです。

TEST =
* Name , Description, SubTree, Alternate, Project
ELEM1, PVSG of ELEM1 , , , TEST

図912.6 生成FT用FTD

FTL

FTLはシンプルなので、エクセルシートで事前生成をする必要はありません。Sheet1のA列のみを以下のようにFTLの3行目の"ELEM1 OR"の次の行からコピーします。

TEST, ELEM1=
ELEM1 OR
C1000
C1001
R1000
R1001
R1002
R1003
C1010
C1011
R1010
R1011
R1012
R1013
^EOS

図912.7 生成FT用FTL

GTD

中間ゲートが無いため本ファイルは不要です。

MARD

MARDを図912.7に示します。

TEST_Subs\TEST.BED
TEST_Subs\TEST.BEI
TEST_Subs\TEST.FTD
TEST_Subs\TEST.FTL

図912.7 ターゲットFT用MARD

---

前のブログ 次のブログ

はじめに

過去記事の再トライアルとなります。なぜ再トライアルかというと、4年が経ちSAPHIREの版数も上がったので、ファイルに互換性が無くなったようです。そのためFault Treeを外部から生成する方法を本記事で確立します。

過去記事で「MAR-D(各種データ)の一括インポートにより、完全なFTが構成できるようです。」と書きましたが、これは変わりません。また対象FTも同一のもの(図911.1)とします。

図911.1 ターゲットのFT

図911.1のFTをテキストファイルで入力するためには

• .BED --- Basic Eventの説明等の記述
• .BEI --- Basic Eventの情報、故障率やミッション時間等
• .FTD --- Fault Treeの説明等の記述
• .FTL --- 木の構造
• .GTD --- Top Event、中間ゲートの説明等の記述
• .MARD --- 上記5種のリストを記述

の6種のファイルが必要です。図911.2～911.6に示すファイルを用意し、そのリストを図911.7のMARDファイルとしてMARDをloadすると、図911.1のFTが生成されました。以下に一つずつ文法例を解説します。先頭に*がある行はコメント行を表します。

BED

図911.2のBEDは基事象の定義で、3種類の基事象の名前と説明を記述します。

*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
BE01 , Failure of 01 , TEST
BE02 , Failure of 02 , TEST
BE03 , Failure of 03 , TEST
TOP , PVSG of top , TEST

図911.2 ターゲットFT用BED

BEI

図911.3のBEIは基事象の故障モデル、故障率、ミッション時間を記述します。赤字は故障率、青字はミッション時間です。

*Saphire 8.2.9
TEST =
* Name ,FdT,UdC ,UdT, UdValue, Prob, Lambda, Tau, Mission, Init,PF, UdValue2, Calc. Prob, Freq, Analysis Type , Phase Type , Project
BE01 , 3, , , 0.000E+000, 0.000E+000, 1.234E-009, 0.000E+000, 1.000E+005, , , 0.000E+000, 1.234E-004, , RANDOM , CD , TEST
BE02 , 3, , , 0.000E+000, 0.000E+000, 2.345E-009, 0.000E+000, 1.000E+005, , , 0.000E+000, 2.345E-004, , RANDOM , CD , TEST
BE03 , 3, , , 0.000E+000, 0.000E+000, 3.457E-009, 0.000E+000, 1.000E+005, , , 0.000E+000, 3.456E-004, , RANDOM , CD , TEST
TOP , 1, , , 0.000E+000, 1.000E+000, 0.000E+000, 0.000E+000, 0.000E+000, , , 0.000E+000, 1.000E+000, , RANDOM , CD , TEST

図911.3 ターゲットFT用BEI

ここで、図911.3中のFdtは、表911.1(一部のみ)により規定される故障計算タイプです。

表911.1

故障計算タイプ記号	故障計算タイプ説明	数値説明
1	確率	DC等の確率
3	指数分布($1-e^{^-\lambda t}$)	故障率$\lambda$、ミッション時間$T_\text{lifetime}$

図911.4はFT全体の定義を示すFTDファイルで、FTの名前と説明を記述します。

TEST =
* Name , Description, SubTree, Alternate, Project
TOP , PVSG of top , , , TEST

図911.4 ターゲットFT用FTD

FTL

図911.5にFTの木構造であるFTLを記述します。

TEST, TOP =
TOP OR TOP0 BE03
TOP0 AND BE01 BE02
^EOS

図911.5 ターゲットFT用FTL

GTD

図911.6のGTDにゲートの名前と説明を記述します。

TEST=
* Name , Description, Project
TOP, PVSG of top, ,TEST
TOP0, DPF of 01 and 02, ,TEST
TOP01, DPF of 01 and 02, ,TEST

図911.6 ターゲットFT用GTD

MARD

最後のMARDを図911.7に示します。前述のように、TESTフォルダのSubsフォルダに各種ファイルをまとめ、一括ロードするためのリストです。

TEST_Subs\TEST.BED
TEST_Subs\TEST.BEI
TEST_Subs\TEST.FTD
TEST_Subs\TEST.FTL
TEST_Subs\TEST.GTD

図911.7 ターゲットFT用MARD

おわりに

ツールの入力としてはDescriptionに日本語が入るようになって便利にはなりました。一方でimportにおいては日本語が化けるため、自動生成の場合、Descriptionに日本語が使用できません。4年前に日本語入力を依頼した時点では、日本語の入力の改修に対してネガティブな返答でしたが、機会があれば要求したいと思います。

---

前のブログ 次のブログ

以下はSAPHIREユーザーズグループのページです。

図910.1 SAPHIREユーザーズグループ

以下にFAQからの抜粋を示します。ユーザ登録やライセンス費用支払いに関するものです。

Q: SAPHIREソフトウェアのコピーを入手するにはどうすればよいですか？
A:

• SAPHIREの最新バージョンは通常、SAPHIREユーザーグループを通じて配布されます。
• SAPHIREユーザーグループへの参加承認を受ける前に、記入・署名済みの非開示契約（NDA）を米国原子力規制委員会（USNRC）に送付し、承認を得る必要があります。
• NRCの公開ウェブサイトにあるObtaining NRC CodesページからSAPHIRE NDAフォームのコピーを入手してください。
• NRCにNDCを提出すると、INLがSAPHIREユーザーグループのメンバーシップを確立します。メンバーにはSAPHIREユーザーグループのウェブサイトへのアクセスが許可され、SAPHIRE 8の最新実行ファイルをダウンロードしたり、カスタマーサポートを受けることができます。カスタマーサポートおよびSAPHIREの最新リリースへのアクセスは、会員期間中継続されます。

Q: 企業が1人のメンバーに支払うが、2人または3人がソフトウェアを使用することは可能でしょうか？
A:

• はい。会員はカスタマーサポートの費用を負担しますので、1つのウェブサイトへのアクセスと1人へのオンコールサポートのみとなります。一部の組織（企業、大学など）では、カスタマーサポートに関する質問をすべて1人の担当者に集約することを選択しています。
• SAPHIREの利用人数は、USNRCとのNDAによって管理されており、SAPHIREユーザーグループの会員数によって管理されているわけではありません。

---

前のブログ 次のブログ

以下に

• 原始の木
• MCS後の木
• MCS及び因数分解した木

の3つの木のレビューロジック図を示します。原始の木は過去記事に詳細が書かれています。

図29.1 3つの木のレビューロジック

• 原始の木 --- これは元々のPart4から作成した木であり、制御のフロー(RBD)を出力から入力まで辿って作成した木です。
• MCS後の木 --- これは原始の木に対してSAPHIREでMCSをとったものです。OR-ANDの2段論理に圧縮されていることがわかります。積項数は当初110でしたが、それを65に枝刈りしました。
• MCS及び因数分解した木 --- 原始の木のMCSを取ってから3次以上のフォールトを枝刈りし、さらに因数分解を行ったものです。これによりAND-ORの形になるように(なるべくANDを上に上げるように)したところ、メインマイコン各部のフォールトとサブマイコン各部のフォールトの組み合わせということがはっきりし、その他PCB上の共通の電源部は一点故障点として表れています。

---

前のブログ 次のブログ

元に戻って最初の論文を見てみたいと思います。元の論文のFTはLFが考慮されていないものでした。これに対して、前稿において、ワーストケース評価をするため、2nd SMのDC(Diagnostic Coverage)をゼロとして評価しました。

これに対して2nd SMのDCを考慮したらどうなるかを前稿と同様の考え方でやってみます。数式やFTの書き換えルールは基本的に前稿を踏襲しますが、IFUモデルとIFRモデルで数式が異なります。いずれにせよ、$K_\text{SM,MPF}=0$とおいたところに仮に$K_\text{SM,MPF}=0.6$と仮定して計算します。

すると、係数$C_\text{SM,MPF}=0.5368$となり、この係数をEBMとOn-line monitorのDPF項に掛けることになるため、そのFTは図219.1のようになります。

図219.1 Fault Tree

図219.2に図219.1のFTの拡大図を示します。C100として上記係数0.5368をかけています。

図219.2 Fault Treeの拡大

MCS分析を実施すると、42個のMCが得られ、3個以上のエレメント故障をカットすると、24個のMCが残ります。結果として、全く変化はありませんでした。

今回カットされた積項を表219.1に示します。加えた定数(赤字)は全て3点故障以上の積項に掛けられており、全てカットされています。ただし、カットされた積項は18個のはずですが、ツールのバグか17個となっています。

表219.1 図219.1のMCSのカット部分

得られたMCSを表219.2に示します。エレメント故障は2以下のみであり、定数を青字で示しています。

表219.2 図219.1のMCS

元々2 outof 4という変則的な2冗長内部のSMなので、IFとSMのANDはそれだけで4エレメント故障の積項となります。従って、この積項に何を追加しても元々消えるべき項でした。

RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。

---

前のブログ 次のブログ

この結果はワーストケースの評価であり、2nd order SMを無視しているものです。従って、この結果をより実際に近づけるには、2nd order SMのDCをFTに入れる必要があります。

まず、数式で書けば、 $$ \begin{eqnarray} \Pr\{\text{TOP Failure}\}=M_\text{PMHF}\cdot T_\text{L}&=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L}) \left[ (1-K_\text{MPF})+K_\text{MPF}\cdot \frac{\tau}{T_\text{L}} \right]\\ &=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L})C_\text{1, 2} \end{eqnarray} $$ ただし $$ K_\text{MPF}=1-(1-K_\text{E1,MPF})(1-K_\text{E2,MPF}) $$ $C_\text{1, 2}$はE1, E2に依存する定数で、 $$ C_\text{1, 2}\equiv(1-K_\text{MPF})+K_\text{MPF}\cdot \frac{\tau}{T_\text{L}} $$

車両寿命$T_\text{L}=15,000[H]$、定期検査周期$\tau=3,420[H]$として、今回のE1, E2のペアで$C_\text{1, 2}$を計算したところ、表217.1に示すようにC1からC9の9種類の定数が得られました。

表217.1

定数記号	定数値
C1	0.2280772
C2	0.2287720
C3	0.2310880
C4	0.2357200
C5	0.2588800
C6	0.3052000
C7	0.3515200
C8	0.5368000
C9	1.0000000

よって、2入力AND項にそれぞれこの定数項を加えて3ANDとすれば、図217.1のようなFTとなります。今回はマニュアル作業により付加しましたが、モデルもしくはツールを開発した暁には自動的に計算が行われる見込みです。

図217.1　2nd order SM効果を追加したFault Tree

このMCSを取得したところ、表217.2の表のような結果となりました。

表217.2　図217.1のMCS

頂上事象侵害確率は$8.321\times 10^{-4}$、PMHFは55.5[FIT]となりました。このように2nd order SMの効果を入れると、PMHFは25%まで低減することがわかります。

RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。

---

前のブログ 次のブログ

前稿で作成したFTLをSAPHIREにインポートすると、図216.1のようなFTが構成されます。MCSの論理式で示されるとおり、2入力ANDの積項が40個、ORで接続されています。

図216.1 MCSのFault Tree

検証としてこのFTのMCSを確認しますが、当然前々稿と同一のMCSになるはずです。インポート前後でMCSは変化しません。表216.1に得られたMCSを示します。

表216.1 MCSのFTをさらにMCS

この頂上事象侵害確率は$3.380\times 10^{-3}$、PMHFは、225[FIT]となりましたが、前回の結果と同一です。

---

前のブログ 次のブログ

SAPHIREのFTL(Fault Tree Language)の文法を図215.1に示します。これで見ると分かるように、ゲートの記述がコメントとして書けるようです。

図215.1 FTLのフォーマット ただし、このように記述しインポートしても、モデルは作成されますがゲートの説明等の記述は入りませんでした。さらに、基事象は全てtoolにより作成済みである必要があります。

調べてみると、FTLのインポートではなく、MAR-D(各種データ)の一括インポートにより、完全なFTが構成できるようです。

図215.2 ターゲットのFT 例えば、図215.2のFTをFlat File (ASCII File)で入力しようとすると、

• .BED --- Basic Eventの説明等の記述
• .BEI --- Basic Eventの情報、故障率やミッション時間等
• .FTD --- Fault Treeの説明等の記述
• .FTL --- 木の構造
• .GTD --- Top Event、中間ゲートの説明等の記述

の5種が少なくとも必要なようです。図215.3～215.7の構文ファイルを用意し、そのリストを図215.8のMARDファイルとしてMARDをloadすると、図215.2のFTが生成されました。

図215.3のBEDは基事象の定義で、3種類の基事象の名前と説明を記述します。

TEST =
* Name , Descriptions , Project
BE01 , Failure of 01 , TEST
BE02 , Failure of 02 , TEST
BE03 , Failure of 03 , TEST

図215.3 ターゲットFT用BED

図215.4のBEIは基事象の故障モデル、故障率、ミッション時間を記述します。赤字は故障率、青字はミッション時間です。

TEST =
* Name ,FdT,UdC ,UdT, UdValue, Prob, Lambda, Tau, Mission, Init,PF, UdValue2, Calc. Prob, Freq, Analysis Type , Phase Type , Project
BE01 , 3, , , , , 1.234E-009, , 1.000E+005, , , , , , , ,
BE02 , 3, , , , , 2.345E-009, , 1.000E+005, , , , , , , ,
BE03 , 3, , , , , 3.457E-009, , 1.000E+005, , , , , , , ,

図215.4 ターゲットFT用BEI ここで、図215.4中のFdtは、表215.1(一部のみ)により規定される故障計算タイプです。 表215.1

故障計算タイプ記号	故障計算タイプ説明
V	数値事象
1	確率
3	指数分布($1-e^{^-\lambda t}$)

図215.5にFT全体の定義として、FTDとして名前と説明を記述します。

TEST=
* Name , Description, Project
TOP ,PVSG of top , ,TEST

図215.5 ターゲットFT用FTD

図215.6にFTの木構造であるFTLを記述します。これは図215.1に文法が書かれています。

TEST, TOP =
TOP OR TOP01 BE03
TOP01 AND BE01 BE02

図215.6 ターゲットFT用FTL

図215.7のGTDにゲートの名前と説明を記述します。

TEST=
* Name , Description, Project
TOP ,PVSG of top , ,TEST
TOP01 , DPF of 01 and 02 , ,TEST

図215.7 ターゲットFT用GTD

上述のように、TESTフォルダのSubsフォルダに、各種ファイルをまとめ、一括ロードするためのリストです。

TEST_Subs\TEST.BED
TEST_Subs\TEST.BEI
TEST_Subs\TEST.FTL
TEST_Subs\TEST.FTD
TEST_Subs\TEST.GTD

図215.8 ターゲットFT用MARD

ここで調査している理由は、SAPHIRE等のFTA toolによりPMHFを正しく計算させたいためです。FTA toolによりPMHFを正しく計算させる手法には2種類あります。

• モデルがPMHF計算に対応　------------　モデルがPMHF計算に対応していれば、パラメータを入力するだけで、モデルがPMHF式を正しく計算します。
• モデルがPMHF計算に非対応　------------　しかしながら、一般的にはモデルがPMHF計算に対応していないため、ユーザがPMHF式に沿うようにFTを組み上げる必要があります。プログラムでFTのサブツリーが自動生成できれば、その労力が大幅に軽減されます。

---

前のブログ 次のブログ

次に、MCSの表から逆にFTを構成します。その理由はFTA tool上でMCSのモデルを修正できるようにするためです。

SAPHIREにおいてFTをインポートするにはFTL(Fault Tree Language)が必要です。そのために、MCSをまずExcel形式でエクスポートし、それをテキストエディタで修正し、以下に示すFTLフォーマットに変換します。

TOP2,TOP-MCS2=
TOP-MCS2 OR TMP1 TMP2 TMP3 TMP4 TMP5 TMP6 TMP7 TMP8 TMP9 TMP10 TMP11 TMP12 TMP13 TMP14 TMP15 TMP16 TMP17 TMP18 TMP19 TMP20 TMP21 TMP22 TMP23 TMP24 TMP25 TMP26 TMP27 TMP28 TMP29 TMP30 TMP31 TMP32 TMP33 TMP34 TMP35 TMP36 TMP37 TMP38 TMP39 TMP40
TMP1 AND M1 M2
TMP2 AND M1 SC2
TMP3 AND SC1 SC2
TMP4 AND M2 SC1
TMP5 AND SA1 SA2
TMP6 AND M1 MCU2
TMP7 AND M2 MCU1
TMP8 AND MCU1 SC2
TMP9 AND MCU2 SC1
TMP10 AND MCU1 MCU2
TMP11 AND I2 M1
TMP12 AND I1 M2
TMP13 AND I1 SC2
TMP14 AND I2 SC1
TMP15 AND I1 MCU2
TMP16 AND I2 MCU1
TMP17 AND I1 I2
TMP18 AND M2 P1
TMP19 AND M1 P2
TMP20 AND P1 SC2
TMP21 AND P2 SC1
TMP22 AND MCU2 P1
TMP23 AND MCU1 P2
TMP24 AND I2 P1
TMP25 AND I1 P2
TMP26 AND D2 M1
TMP27 AND D1 M2
TMP28 AND D1 SC2
TMP29 AND D2 SC1
TMP30 AND D1 MCU2
TMP31 AND D2 MCU1
TMP32 AND D2 I1
TMP33 AND D1 I2
TMP34 AND P1 P2
TMP35 AND CA2 SA1
TMP36 AND CA1 SA2
TMP37 AND D2 P1
TMP38 AND D1 P2
TMP39 AND D1 D2
TMP40 AND CA1 CA2

---

前のブログ 次のブログ

FT(fault tree)構築方式について、いろいろと試行してみます。以下のFTに対して、TOP事象侵害確率及びPMHFを取得します。

• 2nd SM無しのFT
• 2nd SM有りのFT
• 規格式どおりのFT

まずワーストケースとして2nd order SMが無いと仮定した場合のFTを構築します。前稿表212.1のデータに基づき、前稿図212.2のRBDから2nd SM無しの場合のFTを作成すると、図213.1のようになります。

図213.1 EPSシステムのFT

TOP事象を単独で侵害する中間事象は2つあり、ひとつはマイコン制御冗長系の故障、もう一つはセンサ冗長系の故障です。従ってこれらはTOP事象にORゲートで接続されます。マイコン制御冗長系もセンサ冗長系もどちらも冗長系なので、例えばマイコン冗長系であれば、チャネル1とチャネル2の故障はANDゲートで接続されます。チャネルの内部は直列系であるため、チャネルを構成するそれぞれのエレメント故障はORゲートで接続されます。

このFTに対してFTA toolでMCSを取得すると、表213.1のように40個の積項(product term)が得られます。

表213.1 図213.1のFTのMCS

この頂上事象侵害確率は$3.380\times 10^{-3}$、PMHFは、225[FIT]となりました。参照論文では、ミッション時間は15,000時間としています。

---

前のブログ 次のブログ