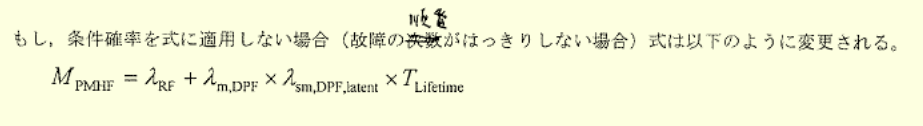ISO/TR 12489:2013(E)において、信頼性用語の定義がまとめてあるため、それを記載します。ただし、弊社の考えを交えており、そのまま引用しているわけではありません。以下に$X_\text{item}$をアイテム$item$の無故障運転継続時間(failure free operating time)とするとき、
信頼度(Reliability)
$$
R_\text{item}(t):=\Pr\lbrace\text{item not failed in }(0, t]\rbrace=\Pr\lbrace\mathrm{item\ up\ at\ }t\rbrace=\Pr\lbrace t\lt X_\text{item}\rbrace
\tag{66.1}
$$
非修理系システムで、時刻$t$までに一度も故障していない確率。非修理系なので、一度でも故障すると故障しっぱなしになるため、一度も故障していない確率です。
不信頼度(Unreliability, Cumulative Distribution Function, CDF)
$$
F_\text{item}(t):=\Pr\lbrace\mathrm{item\ failed\ in\ }(0, t]\rbrace=\Pr\lbrace\mathrm{item\ down\ at\ }t\rbrace=\Pr\lbrace X_\text{item}\le t\rbrace
\tag{66.2}
$$
非修理系システムで、時刻$t$までに故障する確率。
非修理系なので、一度でも故障すると故障しっぱなしになるため、時刻が0からtまでに故障したことがある確率です。等号は有っても無くても値は変わりません。
故障密度(Probability Density, Probability Density Function, PDF)
$$
f_\text{item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace\mathrm{item\ fails\ in\ }(t, t+dt]\cap\mathrm{item\ up\ at\ } t\rbrace}{dt}=\frac{dF_\text{item}(t)}{dt}
\tag{66.3}
$$
又は、微小故障確率形式として、
$$
f_\text{item}(t)dt=\Pr\{\mathrm{item\ fails\ in\ }(t, t+dt]\cap\mathrm{item\ up\ at\ } t\}\\
=\Pr\lbrace t\lt X_\text{item}\le t+dt\rbrace\\
=\Pr\{X_\text{item}\in dt\}
\tag{66.4}
$$
非修理系システムで、時刻$t$で、単位時間あたりに故障する確率。正確には、時刻$t$から$t+dt$までに故障する微小確率を$dt$で割り、単位時間あたりに直したもの。
【証明】
条件付き確率公式及び、確率の加法定理を用いて、
$$
f_\text{item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace t\lt X_\text{item}\le t+dt\rbrace}{dt} \\
=\lim_{dt \to 0}\frac{\Pr\lbrace t\le X_\text{item}\rbrace+\Pr\lbrace X_{item}\le t+dt\rbrace - \Pr\lbrace t\le X_\text{item} \cup X_\text{item}\le t+dt\rbrace}{dt} \\
=\lim_{dt \to 0}\frac{R(t)+F(t+dt)-1}{dt}=\lim_{dt \to 0}\frac{F(t+dt)-F(t)}{dt}=\frac{dF_\text{item}(t)}{dt}
\tag{66.5}
$$
(瞬間)故障率(Failure Rate)
$$
\lambda_\text{item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace\mathrm{item\ fails\ in\ }(t, t+dt]\ |\ \mathrm{item\ not\ failed\ at\ } t\rbrace}{dt}=\frac{f_\text{item}(t)}{R_\text{item}(t)}
\tag{66.6}
$$
非修理系システムで、時刻$t$で稼働している条件において、単位時間あたりに故障する条件付き確率。正確には、時刻$t$から$t+dt$までに故障する条件付き確率を$dt$で割り、単位時間あたりとしたもの。ISO 26262の場合は、確率分布が指数分布のため、故障率は定数として扱います。
【証明】
条件付き確率の式及び、上記$f_\text{item}(t)$の式を用いて
$$
\lambda_\text{item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace X_\text{item}\le t+dt \cap t \le X_\text{item}\rbrace}{dt}\frac{1}{\Pr\lbrace t \le X_\text{item}\rbrace}=\frac{f_\text{item}(t)}{R_\text{item}(t)}
\tag{66.7}
$$
又は、微小故障条件付き確率形式として、
$$
\lambda_\text{item}(t)dt=\Pr\lbrace\mathrm{item\ fails\ in\ }(t, t+dt]\ |\ \mathrm{item\ not\ failed\ at\ } t\rbrace\\
=\Pr\{t\lt X_\text{item}\le t+dt\ |\ t\le X_\text{item}\}\\
=\Pr\{X_\text{item}\in dt\ |\ t\le X_\text{item}\}
\tag{66.8}
$$
稼働度((Point) Availavility)
$$
A_\text{item}(t):=\Pr\lbrace\mathrm{item\ up\ at\ }t\rbrace
\tag{66.9}
$$
修理系システムで、時刻$t$で稼働している確率。
不稼働度((Pont) Unavailavility, PUA)
$$
Q_\text{item}(t):=\Pr\lbrace\mathrm{item\ down\ at\ }t\rbrace=1-A_\text{item}(t)
\tag{66.10}
$$
修理系システムで、時刻$t$で不稼働な確率。
不稼働密度((Point) Unavailability Density, PUD)
$$
q_\text{item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace\mathrm{item\ down\ in\ }(t,t+dt]\cap\mathrm{item\ up\ at\ } t\rbrace}{dt}
=\frac{dQ_\text{item}(t)}{dt}
\tag{66.11}
$$
又は、微小不稼働確率形式として、
$$
q_\text{item}(t)dt=\Pr\lbrace\mathrm{item\ down\ in\ }(t,t+dt]\cap\mathrm{item\ up\ at\ } t\rbrace
\tag{66.12}
$$
時刻$t$で単位時間あたりに不稼働になる確率。正確には、時刻$t$から$t+dt$までに不稼働になる微小確率を$dt$で割り、単位時間あたりに直したもの。failure frequency (故障頻度), unconditional failure intensity (UFI; 無条件故障強度), ROCOF(Rate of OCcurrence Of Failure)とも呼ばれる。
一方、PUDは修理系サブシステムが対象でかつ定期検査修理(PIR)が前提。
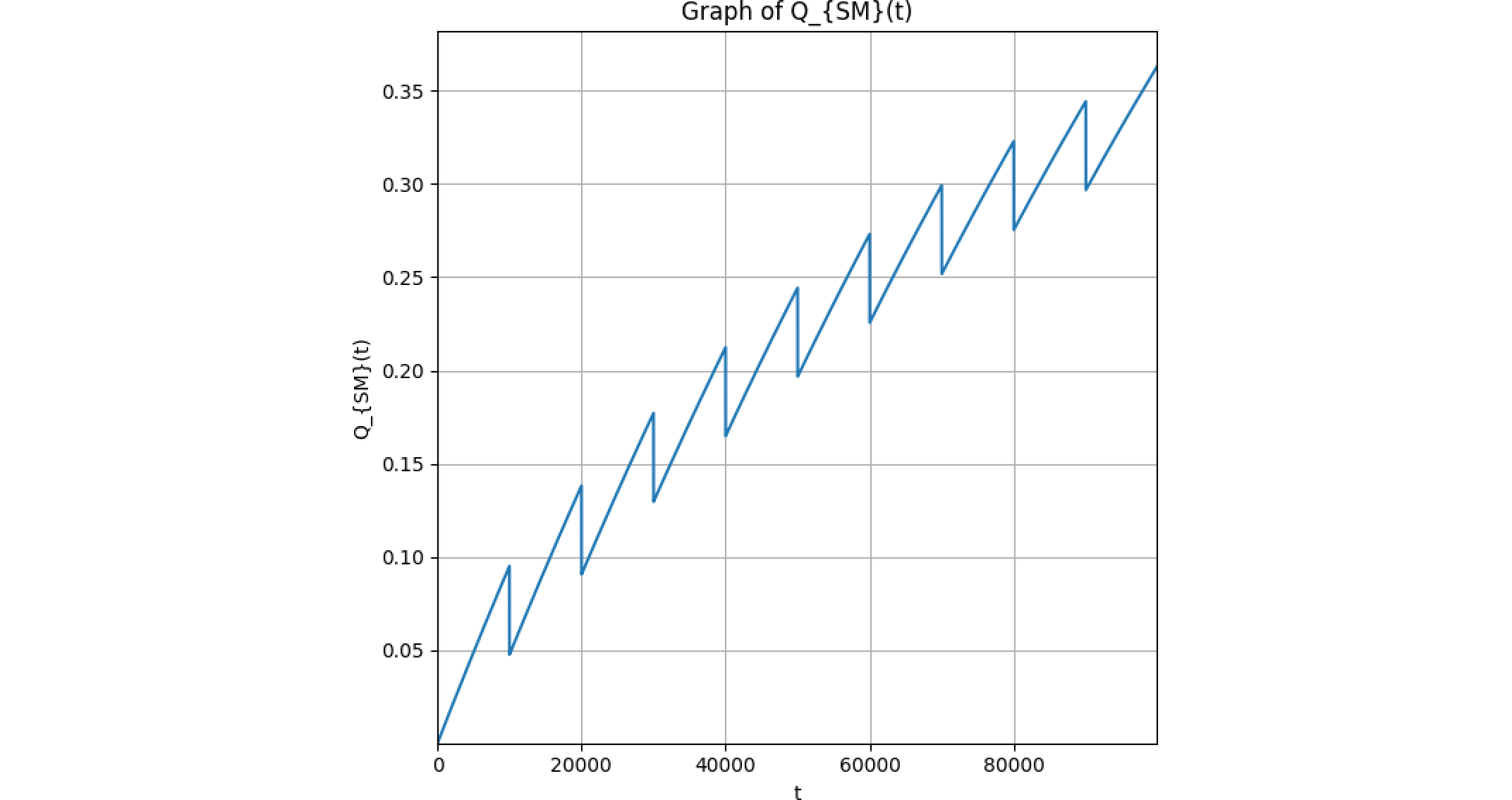
平均不稼働密度(Average PUD)
PUDの車両寿命間$T_\text{lifetime}$の平均値を求めると、平均不稼働密度(Average PUD)は、積分の平均値の定理より、
$$
\overline{q_\text{item}}=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}q_\text{item}(t)dt=\frac{1}{T_\text{lifetime}}Q_\text{item}(T_\text{lifetime})
\tag{66.13}
$$
AROCOFも同様な定義だが、平均不稼働密度(Average PUD)は修理系サブシステムが対象でかつ定期検査修理(PIR)が前提。
PFH(Probability of Failure per Hour)
注意:Probablity of Failure per Hourは古い定義で現在はaverage failure frequency (平均故障頻度), average unconditional failure intensity (平均無条件故障強度)。
$$
PFH:=\overline{q_\text{item}}=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}q_\text{item}(t)dt=\frac{1}{T_\text{lifetime}}Q_\text{item}(T_\text{lifetime})\\
=\frac{1}{T_\text{lifetime}}\Pr\lbrace\mathrm{item\ down\ at\ }T_\text{lifetime}\rbrace, \text{ただし}T_\text{lifetimeは車両寿命}
\tag{66.14}
$$
PMHFも同様の定義だが、平均不稼働密度(Average PUD)は修理系サブシステムが対象でかつ定期検査修理(PIR)が前提。
Vesely故障率(Vesely Failure Rate)
修理系システムで、時刻$t$で稼働している条件において、単位時間あたりに不稼働になる条件付き確率。conditional failure intensity (条件付き故障強度)とも呼ばれる。
$$
\lambda_\text{v,item}(t):=\lim_{dt \to 0}\frac{\Pr\lbrace\mathrm{item\ down\ in\ }(t, t+dt]\ |\ \mathrm{item\ up\ at\ } t\rbrace}{dt}=\frac{q_\text{item}(t)}{A_\text{item}(t)}
\tag{66.15}
$$
以下はISO/TR 12489にはない確率関数です。
修理度(Repairability)
修理系システムで、時刻$t$において不稼働度が修理されるその割合。修理時間は無視できるものとする。
$$
M(t):=\Pr\lbrace\text{repaired at }t\ |\ \text{failed at }t\rbrace\tag{66.16}
$$
 前のブログ
次のブログ
前のブログ
次のブログ