|
31 |
FSMのcall, returnメカニズム |
前記事の共通シーケンスの続きとなります。
FSMのcall, returnメカニズムとして、returnレジスタを設置し、caller側で戻り先ステート(通常は現ステートの次)をreturnに格納しておいて、calleeを呼ぶ機構にしていることは、前記事で記載しました。
単純な場合はこれで動作しますが、callが2段以上になると、returnレジスタが1段であるため、returnレジスタの退避等が必要になります。言うまでもなくプロセッサではスタックがこの自動化を行うわけで、プロセッサの場合の疑似コードを書くと次のようになります。
call CALEE;
:
CALEE:
:
return;
コール、リターンの動作的は、32bitプロセッサの場合、
rs[--sp] ← PC + 4;
PC ← CALEE;
:
CALEE:
:
PC←rs[sp++];
FSMの場合はPCはstateレジスタに相当しますが、それを退避するRS(リターンスタック)配列を設置し、SP(スタックポインタ)も設置します。とはいえ、ハードウェアでありリカーシブコールがあるわけでもないため、4段程度の簡素なスタックとします。2bitですがSPも実装します。実際にはreturnを除いて2段で済んだので(トータルで3段)、SPは1bitとしています。
さらに、上記のようにプリディクリメント、ポストインクリメントの処理とせず、ポスト処理のみとします。その理由はサイクルをかければプリ処理も可能ですが、Verilogが遅延代入であることから、簡単のためポスト処理のみとしています。
また、通常のスタックがpush down(積むと上から下にスタックが伸びる)であるのに比べて、実装するスタックは本当のスタック(地面に積むため、下から上に伸びる)にします。これはどちらでもコストは同等です。
以上のような設計だと、FSMのコールは、図94.1のような疑似コードとなります(caller saved)。
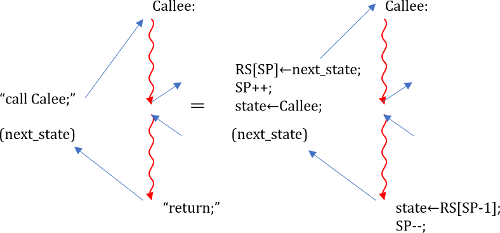
これは全ての場合に動作しますが、リーフコールが多いのにも関わらず、リーフではスタックは不要です。従って、call先を見分ける必要はありますが、コードの効率化を考えて呼び出しをリーフ(緑)コールと非リーフ(赤)コールに分け、リーフをコールする際は以下の図のようなコードを用います。
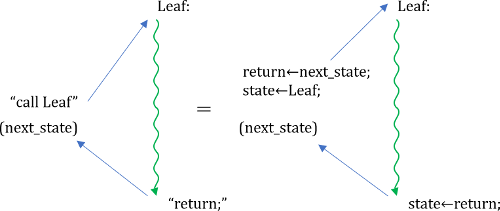
これは、元から使用していたコードと同じものとなります。returnを破壊する一般FSMを赤、returnを破壊しないリーフFSMを緑で表しています。
今回はcaller savedで実装しましたが、callee savedのほうが若干容易かもしれません。caller savedでは呼ぶ前にcalleeがreturnを壊すか壊さないかを調べてからcallしなければならないのに比べて、callee savedであれば、全てreturnレジスタに入れてcallし、callee側でさらに呼ぶときは(つまりreturnを壊す場合は)スタックに入れるという流れであるためです。